北京外国语大学：《运筹学 Operations Research》课程教学资源（课件讲稿）线性代数 Linear Programming（主讲：陈曦）

Linear Programming Xi Chen Department of Management Science and Engineering International Business School Beijing Foreign Studies University 4口40+4之4至，至)只0 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 1/148

Linear Programming Xi Chen Department of Management Science and Engineering International Business School Beijing Foreign Studies University Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 1 / 148

Introduction Introduction The Simplex Method Sensitivity Analysis Duality Theory 4口，40+4立4至，三)及0 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 2/148

Introduction 1 Introduction 2 The Simplex Method 3 Sensitivity Analysis 4 Duality Theory Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 2 / 148

Introduction Example 1 Giapetto's Woodcarving,Inc.,manufactures two types of wooden toys: soldiers and trains.Demand for trains is unlimited,but at most 40 soldiers are bought each week. A soldier sells for $27 and uses $10 worth of raw materials.Each soldier that is manufactured increases Giapetto's variable labor and overhead costs by $14.A train sells for $21 and uses $9 worth of raw materials.Each train built increases Giapetto's variable labor and overhead costs by $10. The manufacture of wooden soldiers and trains requires two types of skilled labor:carpentry and finishing.A soldier requires 2 hours of finishing labor and 1 hour of carpentry labor.A train requires 1 hour of finishing and 1 hour of carpentry labor.Each week,Giapetto can obtain all the needed raw material but only 100 finishing hours and 80 carpentry hours. How to maximize Giapetto's weekly profit? Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 3/148

Introduction Example 1 Giapetto’s Woodcarving, Inc., manufactures two types of wooden toys: soldiers and trains. Demand for trains is unlimited, but at most 40 soldiers are bought each week. A soldier sells for $27 and uses $10 worth of raw materials. Each soldier that is manufactured increases Giapetto’s variable labor and overhead costs by $14. A train sells for $21 and uses $9 worth of raw materials. Each train built increases Giapetto’s variable labor and overhead costs by $10. The manufacture of wooden soldiers and trains requires two types of skilled labor: carpentry and finishing. A soldier requires 2 hours of finishing labor and 1 hour of carpentry labor. A train requires 1 hour of finishing and 1 hour of carpentry labor. Each week, Giapetto can obtain all the needed raw material but only 100 finishing hours and 80 carpentry hours. How to maximize Giapetto’s weekly profit? Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 3 / 148

Introduction o Decision Variables:The decision variables completely describe the decisions to be made.Denote by x1 the number of soldiers produced each week,and by x2 the number of trains produced each week. oObjective Function:The function to be maximized or minimized is called the objective function.Since fixed costs (such as rent and insurance)do not depend on the values of x1 and x2,Giapetto can concentrate on maximizing his weekly profit,i.e.. max 3x1+2x2. ●Constraints: Each week,no more than 100 hours of finishing time may be used. Each week,no more than 80 hours of carpentry time may be used. Because of limited demand,at most 40 soldiers should be produced each week. 2x1+2≤100，为+9≤80，x1≤40. o Sign Restrictions:x≥0andx2≥0. Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 4/148

Introduction Decision Variables: The decision variables completely describe the decisions to be made. Denote by x1 the number of soldiers produced each week, and by x2 the number of trains produced each week. Objective Function: The function to be maximized or minimized is called the objective function. Since fixed costs (such as rent and insurance) do not depend on the values of x1 and x2, Giapetto can concentrate on maximizing his weekly profit, i.e., max 3x1 + 2x2. Constraints: 1 Each week, no more than 100 hours of finishing time may be used. 2 Each week, no more than 80 hours of carpentry time may be used. 3 Because of limited demand, at most 40 soldiers should be produced each week. 2x1 + x2 ≤ 100, x1 + x2 ≤ 80, x1 ≤ 40. Sign Restrictions: x1 ≥ 0 and x2 ≥ 0. Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 4 / 148

Introduction Definition 1.1 A function f(,x2,.·,xn)ofx为，x2,,xn is a linear function if and only if for some set of constants c1,c2,....cn. f (X1,X2,...,Xn)=c1x1 +c2x2+...+CnXn. For any linear function f(x1,x2,...,xn)and any number b,the inequalities f(xM,2,.,xn)≤b and f(灯，x2,.,xn)≥b are linear inequalities. A linear programming problem(LP)is an optimization problem for which we do the following: We attempt to maximize (or minimize)a linear function of the decision variables (objective function). The values of the decision variables must satisfy a set of constraints. Each constraint must be a linear equation or linear inequality. A sign restriction is associated with each variable.For any variable xi, the sign restriction specifies that xi must be either nonnegative (x;>0)or unrestricted in sign (urs). Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 5/148

Introduction Definition 1.1 A function f (x1, x2, . . . , xn) of x1, x2, . . . , xn is a linear function if and only if for some set of constants c1, c2, . . . , cn, f (x1, x2, . . . , xn) = c1x1 + c2x2 + . . . + cnxn. For any linear function f (x1, x2, . . . , xn) and any number b, the inequalities f (x1, x2, . . . , xn) ≤ b and f (x1, x2, . . . , xn) ≥ b are linear inequalities. A linear programming problem (LP) is an optimization problem for which we do the following: 1 We attempt to maximize (or minimize) a linear function of the decision variables (objective function). 2 The values of the decision variables must satisfy a set of constraints. Each constraint must be a linear equation or linear inequality. 3 A sign restriction is associated with each variable. For any variable xi , the sign restriction specifies that xi must be either nonnegative (xi ≥ 0) or unrestricted in sign (urs). Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 5 / 148

Introduction Assumptions oProportionality:The contribution of the objective function from each decision variable is proportional to the value of the decision variable,and so does each linear constraint. o Additivity:The value of the objective function is the sum of the contributions from individual variables,and so does each linear constraint. oDivisibility:Each decision variable be allowed to assume fractional values.A linear programming problem in which some or all of the variables must be nonnegative integers is called an integer programming problem. o Certainty:Each parameter(objective function coefficient,righthand side,and technological coefficient)is known with certainty. 0Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 6/148

Introduction Assumptions Proportionality: The contribution of the objective function from each decision variable is proportional to the value of the decision variable, and so does each linear constraint. Additivity: The value of the objective function is the sum of the contributions from individual variables, and so does each linear constraint. Divisibility: Each decision variable be allowed to assume fractional values. A linear programming problem in which some or all of the variables must be nonnegative integers is called an integer programming problem. Certainty: Each parameter (objective function coefficient, righthand side, and technological coefficient) is known with certainty. Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 6 / 148

Introduction Definition 1.2 The feasible region for an LP is the set of all points that satisfies all the LP's constraints and sign restrictions.Any point that is not in an LP's feasible region is said to be an infeasible point. Definition 1.3 For a maximization problem,an optimal solution to an LP is a point in the feasible region with the largest objective function value.Similarly,for a minimization problem,an optimal solution is a point in the feasible region with the smallest objective function value. o Most LPs have only one optimal solution. Some LPs have no optimal solution. o Some LPs have an infinite number of solutions. Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 7/148

Introduction Definition 1.2 The feasible region for an LP is the set of all points that satisfies all the LP’s constraints and sign restrictions. Any point that is not in an LP’s feasible region is said to be an infeasible point. Definition 1.3 For a maximization problem, an optimal solution to an LP is a point in the feasible region with the largest objective function value. Similarly, for a minimization problem, an optimal solution is a point in the feasible region with the smallest objective function value. Most LPs have only one optimal solution. Some LPs have no optimal solution. Some LPs have an infinite number of solutions. Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 7 / 148

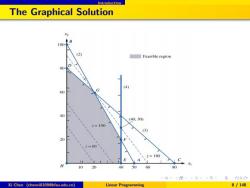
Introduction The Graphical Solution 100 B (2) Feasible region D 80 (4) 60 G 40 (40.30) z=100 (3) 60 2=180 E A C 10 20 40 50 60 80 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 8/148

Introduction The Graphical Solution Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 8 / 148

Introduction Definition 1.4 A constraint is binding if the left-hand side and the right-hand side of the constraint are equal when the optimal values of the decision variables are substituted into the constraint.If they are unequal with respect to the optimal solutions,a constraint is nonbinding. Definition 1.5 A set of points S is a convex set if the line segment joining any pair of points in S is wholly contained in S.For any convex set S,a point P in S is an extreme point if each line segment that lies completely in S and contains the point P has P as an endpoint of the line segment )Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 9/148

Introduction Definition 1.4 A constraint is binding if the left-hand side and the right-hand side of the constraint are equal when the optimal values of the decision variables are substituted into the constraint. If they are unequal with respect to the optimal solutions, a constraint is nonbinding. Definition 1.5 A set of points S is a convex set if the line segment joining any pair of points in S is wholly contained in S. For any convex set S, a point P in S is an extreme point if each line segment that lies completely in S and contains the point P has P as an endpoint of the line segment. Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 9 / 148

Introduction Example 2 Dorian Auto manufactures luxury cars and trucks.The company believes that its most likely customers are high-income women and men.To reach these groups,Dorian Auto has embarked on an ambitious TV advertising campaign and has decided to purchase 1-minute commercial spots on two types of programs:comedy shows and football games. Each comedy commercial is seen by 7 million high-income women and 2 million high-income men.Each football commercial is seen by 2 million high-income women and 12 million high-income men.A 1-minute comedy ad costs $50,000,and a 1-minute football ad costs $100,000.Dorian would like the commercials to be seen by at least 28 million high-income women and 24 million high-income men. How Dorian Auto can meet its advertising requirements at minimum cost? 0Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 10/148

Introduction Example 2 Dorian Auto manufactures luxury cars and trucks. The company believes that its most likely customers are high-income women and men. To reach these groups, Dorian Auto has embarked on an ambitious TV advertising campaign and has decided to purchase 1-minute commercial spots on two types of programs: comedy shows and football games. Each comedy commercial is seen by 7 million high-income women and 2 million high-income men. Each football commercial is seen by 2 million high-income women and 12 million high-income men. A 1-minute comedy ad costs $50, 000, and a 1-minute football ad costs $100, 000. Dorian would like the commercials to be seen by at least 28 million high-income women and 24 million high-income men. How Dorian Auto can meet its advertising requirements at minimum cost? Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 10 / 148