北京外国语大学：《经济数学 Mathematics in Economics》课程教学资源（课件讲稿，下）线性代数 Linear Algebra 第二章 矩阵

第二章矩阵 ◆矩阵的运算 ◆几种特殊矩阵 ◆分块矩阵 ◆逆矩阵 ◆初等矩阵

第二章 矩 阵 矩阵的运算 几种特殊矩阵 分块矩阵 逆矩阵 初等矩阵

§2.1 矩阵的运算 一、矩阵的概念 术语：矩阵（数域F上的矩阵)，记作A,Amxn,(a)mxm 几种特殊矩阵 ()行数与列数都等于n的矩阵A,称为n阶 方阵.也可记作An (2)向量是特殊的矩阵，例如a=(a1,42,…,4n), 为1Xn矩阵. b2 B= 为n×l矩阵

几种特殊矩阵 (1)行数与列数都等于n 的矩阵 A，称为 n 阶 . 方阵.也可记作 An (2)向量是特殊的矩阵, 例如α = (aa a 1 2 ,,, ,  n ) 为1×n矩阵. 1 2 n b b b β       =        为n×1矩阵 §2.1 矩阵的运算 一、矩阵的概念 术语：矩阵（数域F上的矩阵），记作 , ,( ) AA a m n ij m n × ×

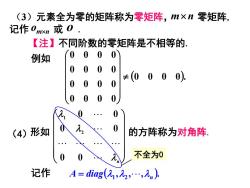
(3)元素全为零的矩阵称为零矩阵，m×n零矩阵， 记作0xm或O 【注】不同阶数的零矩阵是不相等的. 例如 0 ≠(0000 (4)形如 的方阵称为对角阵 不全为0 记作 A=diag(21,元2，…，元n)

（3）元素全为零的矩阵称为零矩阵，m × n 零矩阵, 记作 om×n 或 o . 【注】不同阶数的零矩阵是不相等的. (0 0 0 0). 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ≠              例如                λ n λ λ        0 0 0 0 0 0 2 1 （4）形如 的方阵称为对角阵. 不全为0 记作 ( , , , ). 1 2 n A = diag λ λ  λ

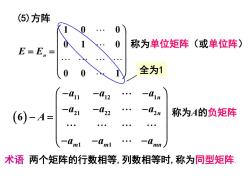
(5)方阵 称为单位矩阵（或单位阵) E=E= 全为1 一1 12 (6)-A= -L21 一L22 称为A的负矩阵 一lmn 术语两个矩阵的行数相等，列数相等时，称为同型矩阵

(5)方阵             = = 0 0 1 0 1 0 1 0 0        E E n 称为单位矩阵（或单位阵） 全为1 术语 两个矩阵的行数相等,列数相等时,称为同型矩阵. ( ) 11 12 1 21 22 2 1 1 6 n n m m mn aa a aa a A aa a   −− −   −− − − = −− −        称为A的负矩阵

矩阵相等的定义 两个矩阵A=(4,)与B=(b,)为同型矩阵，并且对应 元素相等，即a,=b,(i=1,2,…,mj=1,2,…,n) 则称矩阵A与B相等，记作A=B. 1.矩阵的加法 定义设有两个m×n矩阵A=(a人B=(b,)那么矩阵 A与B的和记作A+B，规定为 a11+b1 a2+b2 …L1n+bm a21+b21a2z+b2 A+B= …a2n+b2m +b 说明只有同型矩阵才能进行加法运算

1.矩阵的加法 说明 只有同型矩阵才能进行加法运算.               + + + + + + + + + + = m m m m mn mn n n n n a b a b a b a b a b a b a b a b a b A B        1 1 2 2 21 21 22 22 2 2 11 11 12 12 1 1 设有两个 矩阵 那么矩阵 与 的和记作 ，规定为 m × n A (a ), B (b ), = ij = ij A B A+ B 定义 两个矩阵 为同型矩阵,并且对应 元素相等,即 Aa Bb = = ( ij)与 ( ij) a b (i 1,2, ,m; j 1,2, ,n), ij = ij =  =  则称矩阵A与B相等,记作A = B. 矩阵相等的定义

由矩阵的加法和负矩阵可定义矩阵的减法 411-b1412-b12…41m-bm A-B=A+(-B)= a21-b21a22-b22·42n-b2m am-bmt am2-bm2 …nmn-b, 矩阵加法的运算律 (1)A+B=B+A; (2)(A+B)+C=A+(B+C) (3)A+0=A,A+(-A)=O: (4)A-A=A+(-A)=O

11 11 12 12 1 1 21 21 22 22 2 2 11 22 ( ) n n n n m m m m mn mn ab ab ab ab ab ab AB A B abab ab   −− −   −− − − = +− = −− −        由矩阵的加法和负矩阵可定义矩阵的减法 矩阵加法的运算律 (1) A+ B = B + A; (2)(A+ B) + C = A+ (B + C). (3, ; ) A O AA A O + = +− = ( ) (4) AAA A O − = +− = ( )

2.数与矩阵的乘法 定义数λ与矩阵A的乘积记作A或A几，规定为 /211 212 Main 2L21 λA=A2= l22 λ2n Aa n 【注1】矩阵所有元素的公因子可以提到矩阵符号外 【注2】思考数乘行列式与数乘矩阵的差异：例如 2 2 73 2 -4 4

. 1 1 21 22 2 11 12 1               = = m m mn n n a a a a a a a a a A A λ λ λ λ λ λ λ λ λ λ λ        定义 数λ与矩阵A的乘积记作λA或Aλ,规定为 2. 数与矩阵的乘法 【注1】矩阵所有元素的公因子可以提到矩阵符号外. 【注2】思考数乘行列式与数乘矩阵的差异：例如 12 22 2 4 34 64 = = − 12 24 2 34 68       =   

数乘矩阵的运算律 (设A、B为m×n 矩阵，人，4为数) (1)2(A+B)=A+元B;(2)(2+4)A=2M+A; (3)(4A=(uA): (4)1·A=A. 矩阵加法与数乘矩阵合起来，统称为矩阵的线性运算. 例1矩阵X满足X+2A=B-X,其中 2 ( 求X. 8

数乘矩阵的运算律 矩阵加法与数乘矩阵合起来,统称为矩阵的线性运算. （设 A、B 为 m × n 矩阵，λ ,µ 为数） (3 ; ) (λµ λ µ ) A A = ( ) (1 ; ) λ λλ ( AB A B += + ) (2)(λ + µ)A = λA+ µA; (41 . ) ⋅ = A A 1 1 24 , 1 1 68 A B    − =    =    − 例1 矩阵 X满足 X ABX + =− 2 ，其中 求 X

3.矩阵乘法 引例1 甲、乙两厂，生产三种产品1、川、川， 各厂生产各种产品的产量列为矩阵A, 三种产品单位产量的价格与耗电、耗水、耗油量列为矩阵B 单价耗电耗水耗油 A= 2 3 甲 b b12 b13 22 L23 乙 B= bi b24 I b32 b34 L 分别计算甲厂、乙厂的收入、 耗电， 耗水、耗油总量 br2 bis Bis AB= 213 2 b22 b23 b24 L22 023 b34 01b+412b21+a13b3141b2+a12b22+413b23 41b13+a12b23+a13b341ub14+412b24+413b34 a21b11+2b21+a23b31a21b2+a22b22+a23b32a21b1g+22b23+u23b32a21b14+a22b24+a23b34 “第一行四个元素”为甲厂产品的总收入，总 耗电，总耗水、总耗油量

11 12 13 14 11 12 13 21 22 23 24 21 22 23 31 32 33 34 11 11 12 21 13 31 11 12 12 22 13 23 11 13 12 23 13 33 11 14 12 24 13 34 21 11 22 21 23 31 21 12 22 22 23 32 21 13 bbbb aaa AB bbbb aaa bbbb ab ab ab ab ab ab ab ab ab ab ab ab ab ab ab ab ab ab ab      =      ++ ++ ++ ++ = ++ ++ 22 23 23 32 21 14 22 24 23 34 ab ab ab ab ab     ++ ++   3. 矩阵乘法 引例 甲、乙两厂，生产三种产品Ⅰ、Ⅱ、Ⅲ， 各厂生产各种产品的产量列为矩阵A， 三种产品单位产量的价格与耗电、耗水、耗油量列为矩阵B 分别计算甲厂、乙厂的收入、耗电，耗水、耗油总量. 11 12 13 21 22 23 I II III aaa A aaa   =     甲 乙 单价 耗电 耗水 耗油 11 12 13 14 21 22 23 24 31 32 33 34 bbbb I B b b b b II b b b b III     =   “第一行四个元素”为甲厂产品的总收入,总 耗电,总耗水、总耗油量

矩阵的乘法定义 设A=(an)是一个m×s矩阵，B=(b)是一 个S×n矩阵，规定矩阵A与矩阵B的乘积 是一个mxn矩阵C=(c,),即 A=(aj)mxs B= )sxn b 2 s b = 21 cg=ab,+a,b,++ab,=∑ k=1 (i=1,2,…m5j=1,2,,n), 并把此乘积记作C=AB. 例如G2n=421bn+a2,b2n+…+42.bn=∑2kbm k=

11 22 1 s ij i j i j is sj ik kj k c ab ab ab ab = = + ++ =  ∑ (i = 1,2,m; j = 1,2,,n), 并把此乘积记作 C = AB. 设 是一个 矩阵， 是一 个 矩阵，规定矩阵 与矩阵 的乘积 是一个 矩阵 ，即 ( ) A = aij m × s ( ) B = bij s × n m × n ( )ij C = c A B 矩阵的乘法定义 例如 2 21 1 22 2 2 2 1 s n n n s sn k kn k c ab ab ab ab = = + ++ =  ∑ ( ) A a = ij m s × 11 12 1 21 22 2 1 2 , s s m m ms aa a aa a aa a     =        ( ) B b = ij s n× 11 12 1 21 22 2 1 2 n n s s sn bb b bb b bb b     =       