新疆大学:《材料力学》课程教学资源(PPT课件)第七章 弯曲变形(不含视频演示)

第七章弯曲变形 百嘉道火事
第七章 弯曲变形

第七章弯曲变形 §7-1引言 §7-2挠曲线近似微分方程 §7-3计算梁位移的积分法 §7-5计算梁位移的叠加法 §7-6简单静不定梁 §7-7梁的刚度条件与合理刚度设计 ⊙嘉面人善
第七章弯曲变形 §7-1 引 言 §7-2 挠曲线近似微分方程 §7-3 计算梁位移的积分法 §7-5 计算梁位移的叠加法 §7-6 简单静不定梁 §7-7 梁的刚度条件与合理刚度设计

第七章弯曲变形 引言 87-1引言0 x q 一、挠曲线梁变形后的轴线。 性质:连续、光滑、弹性、极其平坦的平面曲线。 二、挠度横截面形心沿垂直于轴线方向的位移。 用“w”表示。w=w(X)挠度方程 挠度向上为正;向下为负。 ⊙嘉大票
第七章 弯曲变形 §7-1 引 言 一、挠曲线 梁变形后的轴线。 性质:连续、光滑、弹性、极其平坦的平面曲线。 二、挠度 横截面形心沿垂直于轴线方向的位移。 用“w” 表示。 w = w( x ) 挠度方程 挠度向上为正;向下为负。 q F x w x w 引言
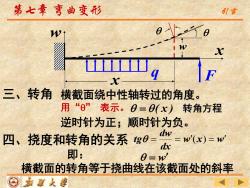
第七章弯曲变形 引言 X 三、转角 横截面绕中性轴转过的角度。 用“0”表示。0=0(x)转角方程 逆时针为正;顺时针为负。 四、挠度和转角的关系gB==w(x)=w dx 即: 0=w' 横截面的转角等于挠曲线在该截面处的斜率 ⊙老道人善
第七章 弯曲变形 三、转角 横截面绕中性轴转过的角度。 用“” 表示。 = ( x ) 转角方程 逆时针为正;顺时针为负。 四、挠度和转角的关系 q F x w x w w x w dx dw tg = = ( ) = 横截面的转角等于挠曲线在该截面处的斜率 即: = w 引言

第七章弯曲变形 龙曲孩近仙般方程 §7-2挠曲线近似微分方程 p(x) W I W X X 一、曲率与弯矩的关系 1M(x) EI. p(x) EI. ⊙嘉道人
一、曲率与弯矩的关系 §7-2 挠曲线近似微分方程 第七章 弯曲变形 q F x w x w ( x ) EIz M( x ) ( x ) 1 = EIz 1 M = 挠曲线近似微分方程
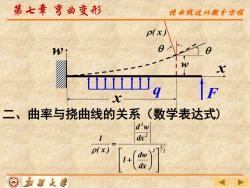
第七章弯曲变形 龙曲残近仙微今方程 p(x) I W x x 二、曲率与挠曲线的关系(数学表达式) dw p(x) 1+ dw ⊙嘉道人薯
w 第七章 弯曲变形 q F x x w ( x ) 二、曲率与挠曲线的关系(数学表达式) 2 3 2 2 2 dx dw 1 dx d w ( x ) 1 + = 挠曲线近似微分方程
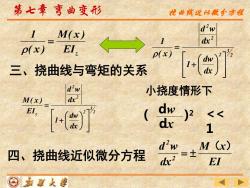
第七章弯曲变形 龙曲孩近仙微分方程 1 M(x) p(x) EI, 三、挠曲线与弯矩的关系 小挠度情形下 M(x) EI, dw << dv 2 1 d'w M(x) 四、挠曲线近似微分方程 =士 dx2 EI ⊙嘉范大事
第七章 弯曲变形 2 3 2 2 2 dx dw 1 dx d w ( x ) 1 + = z EI M( x ) ( x ) 1 = 三、挠曲线与弯矩的关系 2 3 2 2 2 z dx dw 1 dx d w EI M( x ) + = 小挠度情形下 ( dw dx ) 2 << 1 EI M x dx d w 2 2 ( ) 四、挠曲线近似微分方程 = 挠曲线近似微分方程
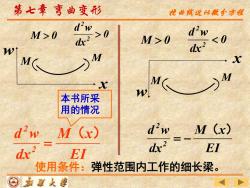
第七章弯曲变形 花曲孩近仙撒今方程 M>0 d'w-0 dx2 M>0 <0 dx2 X 本书所采 用的情况 d2w M(x) dwM(x) EI EI 使用条件:弹性范围内工作的细长梁。 ⊙嘉面人妻
EI M x dx d w 2 2 ( ) = − EI M x dx d w 2 2 ( ) = M 0 M 0 本书所采 用的情况 w x M M w x 使用条件:弹性范围内工作的细长梁。 M M 第七章 弯曲变形 挠曲线近似微分方程 0 dx d w 2 2 0 dx d w 2 2

第七章弯曲变形 计并银公移的积分信 §7-3计算梁位移的积分法 一、积分法 d2w M(x) EIw"(x)=M(x) 2 EI Ew(x)=∫M(x)&+C Ew(x)=∫(M(xxx+Cx+C, 利用梁的位移条件确定式中的积分常数,就得转角 方程0=0x)=w′(x)和挠度方程w=w(x),从而也就 可以求某个具体横截面处的转角和挠度了。这种求转 角和挠度的方法称为积分法。 ⊙嘉大票
第七章 弯曲变形 §7-3 计算梁位移的积分法 一、积分法 EIw(x) = M(x) dx C1 EIw ( x ) = M( x ) + dx C1 x C2 EIw( x ) = ( M( x )dx ) + + 利用梁的位移条件确定式中的积分常数,就得转角 方程 = (x) = w′(x)和挠度方程w = w (x) ,从而也就 可以求某个具体横截面处的转角和挠度了。这种求转 角和挠度的方法称为积分法。 计算梁位移的积分法 EI M x dx d w 2 2 ( ) =
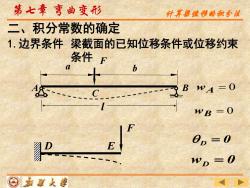
第七章弯曲变形 计其解怪移的积分依 二、积分常数的确定 1.边界条件梁截面的已知位移条件或位移约束 条件 F B W=0 WB=0 E OD-0 WD =0 ⊙嘉面人¥
梁截面的已知位移条件或位移约束 条件 二、积分常数的确定 1.边界条件 第七章 弯曲变形 A B F a b C l wA = 0 wB = 0 wD = 0 D = 0 D E F 计算梁位移的积分法
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 新疆大学:《材料力学》课程教学资源(PPT课件)第四章 扭转(不含视频演示).ppt
- 新疆大学:《材料力学》课程教学资源(PPT课件)第五章 弯曲时的内力(不含视频演示).ppt
- 新疆大学:《材料力学》课程教学资源(PPT课件)第三章 轴向拉压变形(不含视频演示).ppt
- 新疆大学:《材料力学》课程教学资源(PPT课件)第二章 轴向拉压应力与材料的力学性质(不含视频演示).ppt
- 新疆大学:《材料力学》课程教学资源(PPT课件)绪论(负责人:迪丽娜.马合木提,不含视频演示).ppt
- 新疆大学:《材料力学》课程教学资源(作业习题)压杆稳定典型习题解析.pdf
- 新疆大学:《材料力学》课程教学资源(作业习题)超静定问题典型习题解析.pdf
- 新疆大学:《材料力学》课程教学资源(作业习题)强度理论典型习题解析.pdf
- 新疆大学:《材料力学》课程教学资源(作业习题)应力应变状态典型习题解析.pdf
- 新疆大学:《材料力学》课程教学资源(作业习题)弯曲变形典型习题解析.pdf
- 新疆大学:《材料力学》课程教学资源(作业习题)弯曲应力典型习题解析.pdf
- 新疆大学:《材料力学》课程教学资源(作业习题)弯曲内力典型习题解析.pdf
- 新疆大学:《材料力学》课程教学资源(作业习题)扭转典型习题解析.pdf
- 新疆大学:《材料力学》课程教学资源(作业习题)拉伸变形典型习题解析.pdf
- 新疆大学:《材料力学》课程教学资源(作业习题)拉伸应力典型习题解析.pdf
- 新疆大学:《材料力学》课程教学资源(作业习题)材料力学练习册(后付部分题解).doc
- 新疆大学:《材料力学》课程教学实验指导书.doc
- 新疆大学:《材料力学》课程教学资源(教案讲义)第8章 组合变形.doc
- 新疆大学:《材料力学》课程教学资源(教案讲义)第7章 应力和应变分析、强度理论.doc
- 新疆大学:《材料力学》课程教学资源(教案讲义)第6章 弯曲变形.doc
- 新疆大学:《材料力学》课程教学资源(PPT课件)第八章 应力与应变分析(不含视频演示).ppt
- 新疆大学:《材料力学》课程教学资源(PPT课件)第六章 弯曲应力(不含视频演示).ppt
- 新疆大学:《材料力学》课程教学资源(PPT课件)第九章 强度理论(不含视频演示).ppt
- 新疆大学:《材料力学》课程教学资源(PPT课件)第十章 组合变形(不含视频演示).ppt
- 新疆大学:《材料力学》课程教学资源(PPT课件)第十一章 压杆稳定(不含视频演示).ppt
- 新疆大学:《材料力学》课程教学资源(PPT课件)第十三章 交变应力.pps
- 新疆大学:《材料力学》课程教学资源(PPT课件)第十二章 动载荷.pps
- 海南大学:《工程力学》课程教学大纲(负责人:陈超核).pdf
- 海南大学:《工程力学》课程授课教案(I).docx
- 海南大学:《工程力学》课程授课教案(II).docx
- 新疆大学:《结构力学》课程教学大纲(汉)Structure Mechanics.doc
- 《结构力学》课程教学资源(教案讲义)第一章 绪论.doc
- 《结构力学》课程教学资源(教案讲义)第二章 平面体系的机动分析.doc
- 《结构力学》课程教学资源(教案讲义)第三章 静定梁与静定刚架.doc
- 《结构力学》课程教学资源(教案讲义)第四章 实体三铰拱.doc
- 《结构力学》课程教学资源(教案讲义)第五章 静定平面桁架.doc
- 《结构力学》课程教学资源(教案讲义)第六章 虚功原理和结构位移计算.doc
- 《结构力学》课程教学资源(教案讲义)第七章 力法.doc
- 《结构力学》课程教学资源(教案讲义)第八章 位移法.doc
- 《结构力学》课程教学资源(教案讲义)第九章 渐进法.doc
