安徽理工大学：《现代密码学 Modern Cryptography》课程教学资源（实验设计）椭圆曲线加密算法（Elliptic Curve Cryptosystem, ECC）的设计与实现

一、什么是椭圆曲线 ,椭圆曲线是指威尔斯特拉Weierstrass)方程所确定的平面曲线 E:y2+axy+by=x3+cx2+dx+e 其中a,b,c,d,e属于域E,F可以是有理数域、复数域或有限域GF(p)。 椭圆曲线有一个特殊的点，记为O,它并不在椭圆曲线E上，此点称为无限 远的点(the point at infinity)。在xOy平面上，可以看作是平行于y轴的所有 直线的集合的一种抽象。 y2=X3-X y2=X3-X+1

 椭圆曲线是指威尔斯特拉(Weierstrass)方程所确定的平面曲线 E y + axy + by = x + cx + dx + e 2 3 2 : 其中a,b,c,d,e属于域F, F可以是有理数域、复数域或有限域GF(p)。 椭圆曲线有一个特殊的点，记为O，它并不在椭圆曲线E上，此点称为无限 远的点(the point at infinity) 。在xOy平面上，可以看作是平行于y轴的所有 直线的集合的一种抽象

二、有限域GF(p)上的椭圆曲线 ,密码学中普遍采用有限域上的椭圆曲线，它是指椭 圆曲线方程的定义中，所有系数、方程的根都是某 一有限域GF(p)中的元素。其最简单的表示为： E:y2 x3+ax+b(mod p) 也记为Ep(a,b) 其中p是一个大素数，a,b,x,y均在GFp),且满足4a3+27b2(modp)0, 以保证在GF(p)有限域中，E上的所有点构成一个Abel群

 密码学中普遍采用有限域上的椭圆曲线，它是指椭 圆曲线方程的定义中，所有系数、方程的根都是某 一有限域GF(p)中的元素。其最简单的表示为： ( , ) : (mod ) 2 3 E a b E y x ax b p 也记为 p = + + 其中p是一个大素数，a, b, x, y均在GF(p), 且满足4a3+27b2 (mod p)≠0， 以保证在GF(p)有限域中，E上的所有点构成一个Abel群

二、有限域GF(p)上的椭圆曲线 定理：E(4,b)上的点，对于如下定义的加法规则构成 一个Abel群。 (一）加法规则： ① O+0=0; ② 对任意P=(x,y)∈E,(a,b),有P+O=O+P=P; ③ 对任意P=(xy)∈E,(a,b),有P+(-P)=0,即P的逆元为-P=(k,-y) ④ 令P-(x1,y1)∈E,(a,b),Q=(x2,y2)∈E,(a,b),则P+Q=R=(3,3) 其中： X3=2-x1-x2 y2-y ,若P≠Q P = X2-X1 y3=2(x1-X3)-1 3x+0 若P=Q(倍点规则 2y1

定理：Ep (a, b)上的点，对于如下定义的加法规则构成 一个Abel群。 （一）加法规则： ① O+O=O； ② 对任意P=(x,y)∈Ep (a, b), 有P+O=O+P=P; ③ 对任意P=(x,y)∈Ep (a, b), 有P+(-P)=O ，即P的逆元为-P =(x,-y) ④ 令P=(x1,y1) ∈ Ep (a, b)， Q=(x2, y2) ∈ Ep (a, b), 则P+Q=R=(x3,y3) 其中： 3 1 3 1 1 2 2 3 y (x x ) y x x x = − − = − −       = +  − − = , ( ) 2 3 , 1 2 1 2 1 2 1 若 倍点规则 若 P Q y x a P Q x x y y P 

二、有限域GF(p)上的椭圆曲线 定理：E(☑，b)上的点，对于如下定义的加法规则构成 一个Abel群（交换群)。 (一）加法规则： ⑤ 对所有的点P,Q,满足加法交换律，即P+Q=Q+P; ⑥ 对所有的点P,Q,R,满足加法结合律，即P+(Q+R)=(P+Q)+R

定理：Ep (a, b)上的点，对于如下定义的加法规则构成 一个Abel群（交换群）。 （一）加法规则： ⑤ 对所有的点P, Q, 满足加法交换律，即P+Q=Q+P; ⑥ 对所有的点P, Q, R, 满足加法结合律，即P+(Q+R)=(P+Q)+R

二、有限域GF(D)上的椭圆曲线 (二)E,(a,b)上的点在Abel群上加法规则的几何意义 0是单位元； 2 (互为逆元点相加)一条与X轴垂直的线与曲线相交于两个点， 这两个点的横坐标相同，即P=(Xy),Q=(Xy),同时它也与曲线 相交于无穷远点O,因此Q=P。故椭圆曲线的性质决定P与其 逆元成对地出现在椭圆曲线上。 P+Q+0=0

（二）Ep (a, b)上的点在Abel群上加法规则的几何意义 ① O是单位元； ② (互为逆元点相加)一条与X轴垂直的线与曲线相交于两个点， 这两个点的横坐标相同，即P=(x, y), Q=(x, -y), 同时它也与曲线 相交于无穷远点O，因此Q=-P。故椭圆曲线的性质决定P与其 逆元成对地出现在椭圆曲线上

二、有限域GF()上的椭圆曲线 (二)E,(a,b)上的点在Abel群上加法规则的几何意义 ③ (不同点相加)横坐标不同的两个点P,Q相加时，先在它们之间 画一条直线并求直线与曲线的第三个交点R,则P+Q+R=O,即 P+Q=-R. 1 P+Q之值 P+Q+R=0

（二）Ep (a, b)上的点在Abel群上加法规则的几何意义 ③ (不同点相加)横坐标不同的两个点P，Q相加时，先在它们之间 画一条直线并求直线与曲线的第三个交点R, 则P+Q+R=O, 即 P+Q=-R. P+Q之值

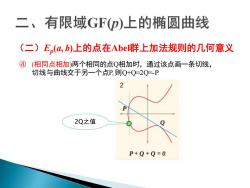
二、有限域GF()上的椭圆曲线 (二)E,(a,b)上的点在Abe群上加法规则的几何意义 ④ (相同点相加)两个相同的点Q相加时，通过该点画一条切线， 切线与曲线交于另一个点P,则Q+Q=2Q=-P. 2 2Q之值 P+Q+Q=0

（二）Ep (a, b)上的点在Abel群上加法规则的几何意义 ④ (相同点相加)两个相同的点Q相加时，通过该点画一条切线， 切线与曲线交于另一个点P, 则Q+Q=2Q=-P. 2Q之值

二、有限域GF(p)上的椭圆曲线 (三)椭圆曲线点乘规则 P=P+P+..+P(k个P相加) ②s,t为整数，(S+t)P=sP+P s(P)=(st)P 定义1椭圆曲线的阶：椭圆曲线E,(a,b)在有限域GF(p)所有离 散点的个数，记为N,称为椭圆曲线的阶。 定义2点的阶：P=(K,y)∈E,(a,b),若存在最小的整数n,使得 nP=O,则称n为椭圆曲线上点P的阶。 定义3生成元：除了无穷远点O之外，椭圆曲线上任何可以 生成所有点的点都可称为椭圆曲线E的生成元，但并不是所 有点都是生成元

（三）椭圆曲线点乘规则 ① kP=P+P+…+P (k个P相加） ② s, t为整数，(s+t)P=sP+tP, s(tP)=(st)P 定义1椭圆曲线的阶：椭圆曲线Ep (a, b)在有限域GF(p)所有离 散点的个数，记为N，称为椭圆曲线的阶。 定义2点的阶：P=(x,y)∈Ep (a, b), 若存在最小的整数n，使得 nP=O, 则称n为椭圆曲线上点P的阶。 定义3生成元：除了无穷远点O之外，椭圆曲线上任何可以 生成所有点的点都可称为椭圆曲线E的生成元，但并不是所 有点都是生成元

三、椭圆曲线上点的计算 1 Hasse's theorem on elliptic curves Hasse's theorem on elliptic curves,also referred to as the Hasse bound,provides an estimate of the number of points on an elliptic curve over a finite field,bounding the value below. If N is the number of points on the elliptic curve E over a finite field with p elements,then Helmut Hasse's result states that lW-(p+1≤2VP

 1、Hasse's theorem on elliptic curves  Hasse's theorem on elliptic curves, also referred to as the Hasse bound, provides an estimate of the number of points on an elliptic curve over a finite field, bounding the value below.  If N is the number of points on the elliptic curve E over a finite field with p elements, then Helmut Hasse's result states that N − ( p +1)  2 p

三、椭圆曲线上点的计算 2,the generation algorithm for pointers on Ep(a,b) Step1:对x=0,l,.,p-1计算x3+ax+b(modp) Step2:对stepl得到的每一结果确定它是否有 个模p的平方根，如果没有，则E,(a,b)中没有以 该结果相应的x为横坐标的点；如果有，就有两 个平方根y和p-y,从而点(xy)和(x,p-y)都是 E(a,b)上的点

 2、the generation algorithm for pointers on Ep (a,b) Step1: 对x=0,1,…, p-1计算x 3+ax+b(mod p) Step2: 对step1得到的每一结果确定它是否有一 个模p的平方根，如果没有，则Ep (a,b)中没有以 该结果相应的x为横坐标的点；如果有，就有两 个平方根y和p-y，从而点(x, y)和(x, p-y)都是 Ep (a,b)上的点