中国地质大学（武汉）：《数字信号处理》课程教学资源（试卷习题）各章习题讲解（2/2）

20.已知序列x(n)=a”u(n),0<a<1,现对于xn) 的z变换在单位圆上N等分抽样，抽样值为 x()=X(e) 试求有限长序列IDFT[X(K)],N点

20. 已知序列 现对于x(n) 的 变换在单位圆上 等分抽样，抽样值为 试求有限长序列 IDFT X k       , 点。    ,0 1, n x n a u n a    z N     2 j k k N N z W e X k X z      N

由x(n)=a"u(n),0<a<1 得e2a 00 n=0 =51T-a a灯 n=0 0w树 n=0 DrTX】-,aeR,o)

( ) ( ), 0 1 n 解：由x n a u n a    1 0 1 ( ) ( ) 1 n n X z x n z az        得  1 1 ( ) ( ) 1 k N k N z W z W X k X z az         1 1 k aWN   1 1 1 1 N Nk N N k N a W a aW        1 0 1 1 N n k N N n aW a      1 0 1 1 N n nk N N n a W a      1 [ ( )] ( ) 1 n N N IDFT X k a R n a   

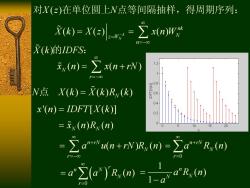
对X(z)在单位圆上N点等间隔抽样，得周期序列： X)=X(ew=∑(ng X(k)的IDFS: 00 xw(n)=∑x(n+rN) 1.2 r=-00 08 N点X(k)=X(K)Rv(k) 0.6 0.4 x'(n)=IDFT[X(k)] 02 =(n)Ry (n) 10 20 =∑aun+rN)Rv(n)=∑a"+vRx(m） -a">(a)'Ry(n)-I-a"Rx(n)

( ) ( ( ) ( ) ) k N nk z W N n X k N W z n X X z x        对 在单位圆上 点等间隔抽样，得周期序列： X k IDFS ( )的 ： ( ) ( ) N r x n x n rN      ( ) ( ) ( ) N X k X k R k 点  N x n IDFT X k '( ) [ ( )]  1 ( ) 1 n N N a R n a   ( ) ( ) N N  x n R n( ) ( ) n rN N r a u n rN R n       0 ( ) n rN N r a R n        0 ( ) r n N N r a a R n    

第四章习题讲解

第四章习题讲解

1.如果一台通用计算机的速度为平均每次复乘5s, 每次复加0.5us,用它来计算512点的DFTx(n),问 直接计算需要多少时间，用FFT运算需要多少时间。 解：(I)直接利用DFT计算： 复乘次数为N2,复加次数为N(N-1)。 复乘所需时间 T=5×10-6×N2=5×10-6×5122=1.31072s 复加所需时间 T=0.5×106×N×(N-1) =0.5×10×512×(512-1)=0.130816s 所以直接利用DFT计算所需时间： T=T+T3=1.441536s

1.如果一台通用计算机的速度为平均每次复乘 ， 每次复加 ，用它来计算512点的 ，问 直接计算需要多少时间，用 运算需要多少时间。 5s 0.5s DFT x n       FFT 解：(1)直接利用 计算： 复乘次数为 ，复加次数为 。 DFT 2 N N N 1 复乘所需时间 6 2 6 2 1 T N s 5 10 5 10 512 1.31072          复加所需时间     6 2 6 0.5 10 1 0.5 10 512 512 1 0.130816 T N N s              所以直接利用DFT 计算所需时间： 1 2 T T T s   1.441536

2)利用FFT计算： 复乘次数为 ，og:V,复加次数为Nog,V。 复乘所需时间 7=5x106×)g,w =5x10×53210g.512=0.0152s 复加所需时间 T=0.5×106×N1og2N =0.5×106×51210g2512=0.002304s 所以用FFT计算所需时间 T=T+T,=0.013824s

复乘所需时间 6 1 2 6 2 5 10 log 2 512 5 10 log 512 0.01152 2 N T N s          6 2 2 6 2 0.5 10 log 0.5 10 512log 512 0.002304 T N N s          复加所需时间 所以用 FFT 计算所需时间 1 2 T T T s    0.013824 (2) 利用 计算： 复乘次数为 ，复加次数为 。 FFT 2 log 2 N N 2 N N log

2.已知X(k),Y(k)是两个N点实序列x(n),y(n)的DFI 值，今需要从X(k),Y(k)求x(n),y(n)的值，为了提 高运算效率，试用一个N点FFT运算一次完成

2.已知 ， 是两个N点实序列 ， 的 值，今需要从 ， 求 ， 的值，为了提 高运算效率，试用一个N点 运算一次完成。 X k  Y k  x n  y n  DFT X k  Y k  x n  y n  IFFT

解：由题意X(k)=DFT[x(n)小，Y(k)=DFT[y(n] 构造序列Z(k)=X(k)+Y(k) 对Z(k)作一次V点FFT可得序列=(n) z(n)=IDFTZ(k) 又根据DFT的线性性质 =(m)=IDFT[Z(K)]=IDFT[X(k)+jY(k) IDFT[X(k)+jTDFT[Y (k) =x(n)+y(n) 而x(n),y(n)都是实序列∴x(n)=Re[(n)] y(n)=Im[z(n】

解：由题意 X k DFT x n Y k DFT y n                   ， 构造序列 Z k X k jY k         对 Z k  作一次N点IFFT可得序列 z n  又根据DFT的线性性质   IDFT X k jIDFT Y k             而 x n  ， y n  都是实序列         Re Im x n z n y n z n            z n IDFT Z k ( )        z n IDFT Z k IDFT X k jY k ( )                    x n jy n    

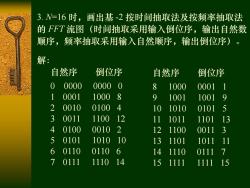
3.N=16时，画出基-2按时间抽取法及按频率抽取法 的FFT流图（时间抽取采用输入倒位序，输出自然数 顺序，频率抽取采用输入自然顺序，输出倒位序)。 解： 自然序 倒位序 自然序 倒位序 0 0000 0000 8 1000 0001 1 0001 1000 8 9 1001 1001 9 2 0010 0100 4 10 1010 0101 5 3 0011 1100 12 11 1011 1101 13 4 0100 0010 2 12 1100 0011 3 5 0101 1010 10 13 1101 1011 11 6 0110 0110 6 14 1110 0111 7 7 0111 1110 14 15 1111 1111 15

3. N=16 时，画出基 -2 按时间抽取法及按频率抽取法 的 FFT 流图（时间抽取采用输入倒位序，输出自然数 顺序，频率抽取采用输入自然顺序，输出倒位序）。 解： 自然序 倒位序 0 0000 0000 0 1 0001 1000 8 2 0010 0100 4 3 0011 1100 12 4 0100 0010 2 5 0101 1010 10 6 0110 0110 6 7 0111 1110 14 自然序 倒位序 8 1000 0001 1 9 1001 1001 9 10 1010 0101 5 11 1011 1101 13 12 1100 0011 3 13 1101 1011 11 14 1110 0111 7 15 1111 1111 15

(1)按时间抽取的基-2FFT流图 N=16=2,L=4 共有L=4级蝶形运算，每级N/2=8个蝶形运算 Xm(k) X(k) X() X() -1 每个蝶形的两节点距离为21，即从第一级到 第四级两节点距离分别为1,2,4,8。 系数W的确定：r=(k)22-m 即的二进制左移L-m位补零

(1) 按时间抽取的基-2FFT流图 16 2 , 4 L N L    共有L = 4级蝶形运算，每级N / 2 = 8个蝶形运算 每个蝶形的两节点距离为 ，即从第一级到 第四级两节点距离分别为1，2，4，8。 1 2 m - 2 ( ) 2 r L m W r k N k L m    系数 的确定： 即 的二进制左移 位补零 r WN 1 ( ) X k m 1 ( ) X j m ( ) X k m ( ) X j m -1