中国地质大学（武汉）：《数字信号处理》课程教学资源（课件讲稿）第三章 离散傅里叶变换 Discrete Fourier Transform（DFT）

第三章离散傅里叶变换 DFT:Discrete Fourier Transform

第三章 离散傅里叶变换 DFT: Discrete Fourier Transform

一、Fourier变换的几种可能形式 时间函数>频率函数 连续时间、连续频率一傅里叶变换 连续时间、离散频率一傅里叶级数 离散时间、连续频率一序列的傅里叶变换 离散时间、离散频率一离散傅里叶变换

一、Fourier变换的几种可能形式 时间函数 频率函数 连续时间、连续频率—傅里叶变换 连续时间、离散频率—傅里叶级数 离散时间、连续频率—序列的傅里叶变换 离散时间、离散频率—离散傅里叶变换

连续时间、连续频率一傅里叶变换 X(j)=x(t)e-dr x()=X(Q)ed x(j2) 时域连续函数造成频域是非周期的谱， 而时域的非周期造成频域是连续的谱密度函数

连续时间、连续频率—傅里叶变换 时域连续函数造成频域是非周期的谱， 而时域的非周期造成频域是连续的谱密度函数。 ( ) ( ) j t X j x t e dt        1 ( ) ( ) 2 j t x t X j e d        

连续时间、离散频率一傅里叶级数 ()d x() x(0)=∑X(jk2,eau X(jk2o) 时域连续函数造成频域是非周期的谱， 而频域的离散对应时域是周期函数

连续时间、离散频率—傅里叶级数 时域连续函数造成频域是非周期的谱， 而频域的离散对应时域是周期函数。 0 0 0 / 2 0 / 2 0 1 ( ) ( ) T jk t T X jk x t e dt T       0 0 ( ) ( ) jk t k x t X jk e      

离散时间、连续频率一序列的傅里叶变换 xnT)或x(n) X(e)=∑x(n)eom n=-00 -2T 0T 3T s()x(e"odo -2-101234 lX(ePTI或I X(e) 0 -2π 2元 时域的离散化造成频域的周期延拓， 而时域的非周期对应于频域的连续

离散时间、连续频率—序列的傅里叶变换 时域的离散化造成频域的周期延拓， 而时域的非周期对应于频域的连续 ( ) ( ) j j n n X e x n e        1 ( ) ( ) 2 j j n x n X e e d         

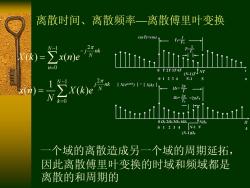
离散时间、离散频率一离散傅里叶变换 x(nT)=x(n) n=0 T2T3T4T (N1)7JW7 01234 N-IN N k=0 2w=2红=2xF0 T Immim 020226320420 01234 N-1 N (N-1)2 一个域的离散造成另一个域的周期延拓， 因此离散傅里叶变换的时域和频域都是 离散的和周期的

离散时间、离散频率—离散傅里叶变换 一个域的离散造成另一个域的周期延拓， 因此离散傅里叶变换的时域和频域都是 离散的和周期的 1 2 0 ( ) ( ) N j nk N n X k x n e      1 2 0 1 ( ) ( ) N j nk N k x n X k e N     

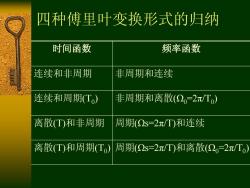
四种傅里叶变换形式的归纳 时间函数 频率函数 连续和非周期 非周期和连续 连续和周期(T) 非周期和离散(2,2π/T0) 离散(T)和非周期 周期(2s=2元/T)和连续 离散(T)和周期(T,)周期(2s=2/T)和离散(2,2π/T0)

四种傅里叶变换形式的归纳 时间函数 频率函数 连续和非周期 非周期和连续 连续和周期(T0 ) 非周期和离散(Ω0=2π/T0 ) 离散(T)和非周期 周期(Ωs=2π/T)和连续 离散(T)和周期(T0 ) 周期(Ωs=2π/T)和离散(Ω0=2π/T0 )

二、周期序列的DFS及其性质 周期序列：x(n)=(n+rN) r为任意整数N为周期 连续周期函数： 元(t)=元(t+kT)T为周期 ,()=∑A(K)e 基频：2=2π/T k=-o0 k次谐波分量：ek2, N为周期的周期序列： 基频：0，=2π/N (n）)=∑A(k)en k次谐波分量：ekoo” k=-o0

二 、周期序列的DFS及其性质 ( ) ( ) x n x n rN r N 周期序列：   为任意整数 为周期 0 0 0 ( ) ( ) ( ) ( ) a a jk t a k x t x t kT T x t A k e        连续周期函数： 为周期 0 0 0 2 / jk t T k e   基频：  次谐波分量： 0 ( ) ( ) jk n k N x n A k e      为周期的周期序列： 0 0 2 / jk n N k e  基频：   次谐波分量：

周期序列的DFS正变换和反变换： 0-DSu-2e六-足wm W-1 n=0 n=0 -风-2e2 k=0 2π 其中：丙，=e

周期序列的DFS正变换和反变换： 1 1 2 0 0 ( ) [ ( )] ( ) ( ) N N j nk N nk N n n X k DFS x n x n e x n W            1 1 2 0 0 1 1 ( ) [ ( )] ( ) ( ) N N j nk N nk N k k x n IDFS X k X k e X k W N N            2 j N W e N   其中： 

例：已知序列x()是周期为6的周期序列， 如图所示，试求其DFS的系数。 解：根据定义求解 15 14 12 W-1 (K)=∑n)Ww 10 10 10 n=0 5 -∑n)W n=0 5 0 5 10 15 n =14+12e *+10e 6 +8e +6e总 +10e X(0)=60X(1)=9-3V3 (2)=3+j√3 x(3)=0(4)=3-3X(5)=9+3√3

x n( ) 6 DFS 例：已知序列 是周期为 的周期序列， 如图所示，试求其 的系数。 1 0 ( ) ( ) N nk N n X k x n W     解：根据定义求解 5 6 0 ( ) nk n x n W    2 2 2 6 6 2 2 2 3 4 5 6 6 6 14 12 10 8 6 10 j k j k j k j k j k e e e e e                 (0) 60 (1) 9 3 3 (2) 3 3 (3) 0 (4) 3 3 (5) 9 3 3 X X j X j X X j X j          