南阳师范学院：《高等数学》课程教学资源（课件讲稿）第七章 向量代数与空间解析几何 §7.1 向量及其线性运算

第七章向量代数与空间解析几何 向量及有关概念 向量代数 向量的线性运算 数量积向量积及混合积 空间直角坐标系 空问解 平面与空间直线 析几何 旋转曲面与二次曲面

向量及有关概念 向量代数 向量的线性运算 数量积向量积及混合积 空间直角坐标系 空间解 析几何 平面与空间直线 旋转曲面与二次曲面 第七章 向量代数与空间解析几何

§7.1向量及其线性运算 主要 内容 向量及有 向量的加 关的概念 减法 数乘向量

主 要 内 容 数乘向量 向量及有 关的概念 向量的加 减法 §7.1 向量及其线性运算

一、向量及与向量有关的概念 向量的模 单位向量 零向量 两相等向 两向量 量 向量的 垂直 两互为反向 定义及表示 向量共面 量 两向量的夹 角 两向量平行

一、向量及与向量有关的概念 向量的模 单位向量 零 向 量 向量的 定义及表示 两向量的夹 角 两向量平行 两相等向 量 两互为反向 量 两向量 垂直 向量共面

二、向量的加减法 1.向量的加法（三角性法则） 2.向量的减法 设已知向量ā，b,以空间任意一点 规定两个向量的a与6的差 A为始点，连接作AB=ā，BC=b, a-b=a+(-b) c-a+b 由两向量a与6求它们差a-b的. 运算叫作向量的减法 B 连接AC,那么向量AC=c称为向量 a与b的和，记作c=a+b.由两向量 对任意的三点AB,C均有 a与b求它们和a+b的运算叫作向 AC=AB+BC,AC-AB=BC 量的加法

二、向量的加减法 1. 向量的加法（三角性法则） 2. 向量的减法 设已知向量 a,  b  ,以空间任意一点 A 为始点，连接作 AB a  , BC b  , a A B C b c a b   连接 AC ,那么向量 AC c  称为向量 a  与 b  的和，记作 c a b      .由两向量 a  与b  求它们和 a b    的运算叫作向 量的加法. 规定两个向量的a与b 的差 a b a b    ( ) 由两向量a 与b  求它们差a b  的. 运算叫作向量的减法. 对任意的三点 A,B,C 均有 AC AB BC   , AC AB BC  

二、向量的加减法 3.平行四边形法则 4.向量加法的运算法则 当向量ā与b不共线时，在空间中 对于任意的向量a,b我们有 任意取一点A,作AB=a,AD=b (1)a+0=a a+(-a列)=0 D a+h (2)交换律a+b=b+a B (3)结合律a+)+c=a+6+c) 以AB、AD为邻边作一平行四边形， ABCD,那么对角线向量 注记3：向量a,b,a+b,a-b共面 AC=AB+AD=a+b la-≤a+≤a+ DB=AB-AD=a-6

二、向量的加减法 3. 平行四边形法则 4. 向量加法的运算法则 当向量 a  与b  不共线时, 在空间中 任意取一点 A ,作 AB a AD b   , A B D C a b a b  以 AB、 AD为邻边作一平行四边形, ABCD,那么对角线向量 AC AB AD a b     DB AB AD a b     对于任意的向量a, b  我们有 （1） a a     0  ( ) 0    a  a  （2）交换律 a b b a        （3）结合律a b c a b c            注记 3：向量a b a b a b , , ,   共面 a b a b a b     

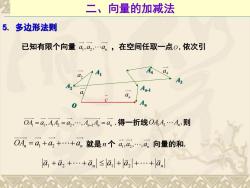
二、向量的加减法 5. 多边形法则 已知有限个向量a,a,…a,,在空间任取一点0，依次引 0A=a,44=4,…,4,-14,=a,得一折线044…An,则 OAn=a+a2+…+an就是n个a,a,…,an向量的和. a1+a2+…+an≤a+a2+…+an

A1 A2 A3 A4 An-1 1 a 4 a 2 a n a c 已知有限个向量 1 2 , , n a a a ，在空间任取一点O ,依次引 1 1 1 2 2 1 , , , OA a A A a A A a    n n n  , 得一折线OA A A 1 2 n , 则 就是n 个 1 2 , , , n OA a a a n n     1 2 a a a 向量的和. 5. 多边形法则 O An 二、向量的加减法 a a an    1  2    a a an     1  2   

三、向量与数的乘法 1.数乘：实数1与向量ā的乘积是一个向量，记作1a, (1)模=2a; (2)2a的方向：1>0时，与a同向； 入<0时，与ā相反. 几=0时， 2ā=0，方向任意， 我们把这种运算叫做数量乘向量，简称数乘， 注记4：与非零向量ā同方向的单位向量。园

（1）模 a   =  a  ; （2） a   的方向:   0时，与a  同向；   0时， 与a  相反. 我们把这种运算叫做数量乘向量，简称数乘. 1.数乘： 实数 与向量 a  的乘积是一个向量,记 作 a   , 三、向量与数的乘法   0时， 0   a  ，方向任意， 注记 4：与非零向量 a 同方向的单位向量 a a e a 

三、向量与数的乘法 2. 数乘的运算规律 对于任意的实数2，u和任意的向量ā，b我们有 (1)1a=a,(-1)a=-d (2)关于数因子的结合律(ua)=()a (3)第一分配率(+)a=2ā+a (4)第二分配率（ā+b)=1ā+5

2. 数乘的运算规律 对于任意的实数, 和任意的向量 a  ， b  我们有 （1） a a   1  ，( 1)     a a （2）关于数因子的结合律    ( ) ( ) a a  （3）第一分配率 a a a    (  )     （4）第二分配率 a b a b     (  )     三、向量与数的乘法

三、向量与数的乘法 定理1：向量b与非零向量ā平行的充要条件是存在唯一的实数2 使b=a. 注记5：设点0及单位向量确定的数轴为Ox轴，那么对于 数轴上的任意一点P,则存在唯一的实数x,使得 OP=xi 点P分向量OP实数x 因此定义实数x为数轴上点P的坐标， 由此可得数轴上点P的坐标为x的充要条件是OP=xi

定理 1：向量b 与非零向量 a 平行的充要条件是存在唯一的实数 使b a   . 三、向量与数的乘法 注记 5： 设点O及单位向量i  确定的数轴为Ox 轴，那么对于 数轴上的任意一点P ，则存在唯一的实数x，使得 OP xi  点P 向量OP  实数x 因此定义实数 x 为数轴上点 P 的坐标. 由此可得数轴上点 P 的坐标为 x 的充要条件是OP xi 

四、课堂训练 (1)若AB=a+5b,BC=-2a+86,CD=3a-36,则下列说法错误的是 (A)AD与AB共线 (B) D与B反方向 (C) A,B,D三点共线 (D) AD=26 (2)若M,N分别是△4BC边AB,AC的中点，则MN= BC (B) 1-2 (C)1 (D)-1 (3)在平行四边形ABCD中，下列说法不一定正确的是 (A) AD与BC是相等的向量 (B) AB与CD是互为反向量 (C) AD与BC的夹角为0 (D)AB 与cD夹角为π (E) AD BC,AB CD (F)AB与CD垂直

（1）若 AB a b BC a b CD a b        5 , 2 8 , 3 3 ,则下列说法错误的是 （A） AD 与 AB 共线 （B） AD 与 AB 反方向 （C） A B D , , 三点共线 （D） AD  2 AB 四、课堂训练 （2）（2）若M N, 分别是ABC边 AB AC , 的中点，则 MN  BC （A）- 1 2 （B） 1 2 （C）1 （D）-1 （2）（3）在平行四边形 ABCD中，下列说法不一定正确的是 （A） AD 与 BC 是相等的向量 （B） AB 与 CD 是互为反向量 （C） AD 与 BC 的夹角为 0 （D） AB 与CD夹角为 （E） AD BC ， AB CD （F） AB 与CD垂直