南阳师范学院：《高等数学》课程教学资源（课件讲稿）第八章 多元函数微分法及其应用 第四节 多元复合函数的求导法则

§8.4多元复合函数的求导法则 主要 内容 中间变量为 中间变量为多 元函数 复合函数 元的函数 的求导法则 的求导法则 中间变量既 有一元函数 又有多元函 数的求导法则

中间变量为一 元函数 的求导法则 中间变量为多 元的函数 的求导法则 主 要 内 容 §8.4 多元复合函数的求导法则 复合函数 中间变量既 有一元函数 又有多元函 数的求导法则

复合函数的中间变量为一元函数的求导法则 设z=sin(u+y cos(u+ du u=x,v=x2 猜想1（1)函数u=p(x),v=w(x)在点x处可导 (2)函数z=f(u,v)在相应点(u,v)处 z=sin(x+x2 cos(u+ = dv =2X 0z 0z 具有连续的偏导数 u'ov 则复合函数z=f几p(x),yW(x】在点x处可导 器-+2eas(r+ 且有 oz du oz dv ou dx ov dx =1+2x)c0s(x+x dz az du + Oz dv dx u dx av dx

一、复合函数的中间变量为一元函数的求导法则   2 sin , z u v u x v x     设   2 z x x   sin   2 (1 2 )cos z x x x x      cos , 1   z du u v u dx      cos , 2   z dv u v x v dx        2 (1 2 )cos z du z dv x x x u dx v dx           （2）函数 z f u v  ( , ) 在相应点(u,v) 处 具有连续的偏导数 , , z z u v     则 复合函数 z f x x  [ ( ), ( )]   在点 x 处可导 猜想 1（1）函数u  (x),v (x)在点 x 处可导 且有 dz z du z dv dx u dx v dx         dz z du z dv dx u dx v dx        

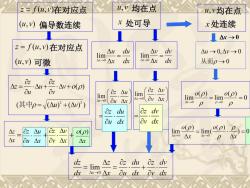
z=f(,v)在对应点 ,v均在点 山，P均在点 (u,)偏导数连续 x处可导 x处连续 △x→0 z=f(u,)在对应点 △udu △dw △u→0，△y→0 lim lim (u,)可微 Ar-0△x dx △r-0△xdx 从而p→0 O z.a+2.△v+o(p) 02 △z= o Ov z△u Oz△y lim lim lim o(p) =lim o(p) Ar>0 Ov△x =0 △x->0 (其中p=V(△)2+（△）2) ou△x △r0 P→0 Oz du oz dv Bu dx Ov dx △z 0z△u △v o(p) lim o(p)=lim( (p).P)=0 Ax0△x r→0 ou△x p△x △x △x △x dz =lim △z oz du,Oz dv △r→0△x Ou dx ov dx

均在点 处连续 在对应 点 偏导数连续 x 0 在对应 点 可微 均在点 处可导

复合函数的中间变量为一元函数的求导法则 定理1若（1)u=p(x),v=W(x)在点x处可导 推广1设n元函数w=f(4,2,,n) (2)函数z=f(u,v)在相应点(u,v)处 4,=4(x),(i=1,2,…,n) 0z 0z 具有连续的偏导数 则 =.d dau,d 则复合函数z=fp(x),W(x】在点x处可导且有 Oz du oz dv dx au dx av dx 注记：求z=fLp(x),yW(x】导数的步骤 第一步：分析变量关系，找出层次 Oz B du dy 第二步：求及 do du o dv 分段用乘，分叉用加 第三步：代入公式kla 单路全导，叉路偏导 第四步：消去中间变量，并整理化简

一、复合函数的中间变量为一元函数的求导法则 （2）函数 z f u v  ( , ) 在相应点(u,v) 处 具有连续的偏导数 , , z z u v     则 复合函数 z f x x  [ ( ), ( )]   在点 x 处可导且有 定理 1 若（1）u  (x),v (x)在点 x 处可导 dz z du z dv dx u dx v dx        z u v x x 分段用乘，分叉用加 单路全导，叉路偏导 推广 1 设 n 元函数 ( , , , ) u1 u2 un w  f  ( ) ,( 1,2, , ) u u x i n i i    则 1 n i i i dz z du dx u dx       u1 u2 z x x  u n x 注记：求 z  f[ (x),(x)]导数的步骤 第一步：分析变量关系，找出层次 第二步：求 , z z u v     及 , du dv dx dx 第三步：代入公式  dx dz dx dv v z dx du u z        第四步：消去中间变量 ，并整理化简

、复合函数的中间变量为一元函数的求导法则 例1：设z=u2v+3w,u=e,v=sinx 例2：设z='(u>0,u≠1)，如果函数 求全导数 u=u(x),v=v(x)均可导，求复合函数 解： =2+3v (1)显然u 解：显然 =, =t'lnw O C2=+12w V d 所以 d=o.du odhy dx ou dx Ov dx du dx dx =COSx vu"-1 du +u'Inu dv dx dx (2)代入 会在气我得 =u" v du dv 东-r+n)p++1m)sx u dx dx =(2e'sinx+3sin'x)e =2u(x)() ()+v()() +(e+12e'sin'x)cosx u(x)

一、复合函数的中间变量为一元函数的求导法则 例 1：设 2 4 3 , , sin x z u v uv u e v x     求全导数 dz dx z u v x x 解：（1）显然 4 2 3 z uv v u     2 3 12 z u uv v     , cos du dv x e x dx dx   （2） 代入  dx dz dx dv v z dx du u z        得     4 2 3 2 3 12 cos dz x uv v e u uv x dx       4 2 sin 3sin x x   e x x e   2 3 12 sin cos x x   e e x x 例 2：设 ( 0, 1) v z u u u    ，如果函数 u u x v v x   ( ), ( ) 均可导，求复合函数 z u v x x 解：显然 1 , ln z z v v vu u u u v        所以  dx dz dx dv v z dx du u z        1 ln v v du dv vu u u dx dx   ln v v du dv u u u dx dx         ( ) ( ) ( ) ( ) ( )ln ( ) ( ) v x v x u x u x v x u x u x          

二、复合函数的中间变量为仅多元函数的求导法 定理2若（1)u=p(x,y),v=W(x,y)在在点 推广2设函数u=p(x,yz),v=(x,y,) w=f(u,v) (x,y)处对x,y偏导数都存在 则 w Ow.Ouow.ov (2)函数z-f(u,v)在相应点(u,v)处 Ox Ou ax Ov Ox OwOw Ou Ow Ov 8z 82 具有连续的偏导数a ay Ou dy ov ay Owow ou Ow Ov Oz Ou oz Ov Oz 则复合函数z=f[p(x,y),yW(x,y)]在点(x,y)处偏导数 =等存在，且 推广3设函数u=u(x,y),V=v(x,y),w=w(x,y) 2= Oz 函数w=fu(x,y),(x,y),wx,y],则 e 0+02.oy Ou ax av Ox 8z Ou Oz 0v 6z Ow a2= Oz Ou Oz Ov Ox Ou ax oy ax ow ax ay ou oy Ov ay 分段用乘，分叉用加 dzdz ou dz dy 6z ow 单路全导，叉路偏导 oy ou dy ov dy ow by

二、复合函数的中间变量为仅多元函数的求导法则 定理 2 若（1）u x y v x y     ( , ), ( , ) 在在点 推广 2 设函数 u x y z v x y z     ( , , ), ( , , ) ( , ) x y 处对 x y, 偏导数都存在 （2）函数 z f u v  ( , ) 在相应点(u,v) 处 具有连续的偏导数 , , z z u v     则复合函数 z f x y x y  [ ( , ), ( , )]   在点( , ) x y 处偏导数 , z z x y     存在，且 z x    z u z v u x v x            z y    z u z v u y v y            z u v x y x y 分段用乘，分叉用加 单路全导，叉路偏导 . w w u w v x u x v x               则 . w w u w v y u y v y               . w w u w v z u z v z               u v x y z z y w w f u v  ( , ) 推广 3 设函数 u u x y v v x y w w x y    ( , ), ( , ), ( , ) 函数 w f u x y v x y w x y  [ ( , ), ( , ), ( , )]，则 z z u z v z w x u x v x w x                     z z u z v z w y u y v y w y                    

二、复合函数的中间变量为仅多元函数的求导法则 例3设z=e“sinv,u=y,v=x+八，求 OE Oz 例4：设z=f(x2-y,e")，求x =e"sinv, 解：显然 -=e"cosy a 解：设u=x2-y2,v=e,则2=fu,) O ou =y, =X, Ox dy Ou=2x, O ou=2y. a =1, d =1 Ox y Ov =e", =xev, dx dy 2-正.ou+2.oy 所以 所以 Ox Ou ax Ov Ox =e"sinv.y+e“cosv.1 -影0+g=2地头 Q ou =e[ysin(x+y)+cos(x+)] =2xfx2-y2,e")+e"fx2-y2,e）) -2.u+02.y Ox ou dy ov ay =f.04+0f.a =-2yg+e dy au ay av ay =e"sinv.x+e“cosv.l =e[xsin(x+)+cos(x+)] =-2fx2-y2,e)+xe"f(x2-y2,e)

例 3 设 z e sin v, u  u  xy,v  x  y,求 , . y z x z     例 4：设 2 2 ( , ) xy z f x y e   ，求 , . y z x z     z u v x y x y 解：显然 sin , z u e v u    cos z u e v v    , u y x    , u x y    1, v x    1 v y    所以 z x    z u z v u x v x            [ sin( ) cos( )] xy     e y x y x y z x    z u z v u y v y            [ sin( ) cos( )] xy     e x x y x y 解： 设 2 2 , xy u x y v e    ，则 z f u v  ( , ) 所以 z f u f v x u x v x               2 2 2 2 1 2 2 ( , ) ( , ) xy xy xy     xf x y e ye f x y e   . 2 z f u f v f f xy y xe y u y v y u v                      2 2 2 2 2 ( , ) ( , ) 1 2 xy xy xy      yf x y e xe f x y e   2 , u x x    2 , u y y     , v xy ye x    , v xy xe y    二、复合函数的中间变量为仅多元函数的求导法则 sin cos 1 u u     e v y e v sin cos 1 u u     e v x e v 2 xy f f x ye u v      

复合函数的中间变量既有一元又有多元函数的求导法则 定理3若（1)u=p(x,y)在点(x,y)处偏导数 0z 0z 例5 设：=arcsin,其中u=xe,v=广，求' 存在，v=W(y)在点y处可导 解：显然 u V-2 0w√1-2v2 (2)函数z=f(u,v)在相应点(w,v)处 82 8z ou ou 具有连续的偏导数ra =xe 则复合函数z=f[p(x,y),W(y)]在点(x,y)处偏导 所以2=立.u e'= yer V1-2v2 VI-x2ye2y 等存在，且 数 OzOz ou oz dy ay ou dy ov dy a2- Oz Ou Ox Ou ax ·xe+ 2y V1-2v2 V1-2v2 OO.Ou oe dy (y+2)xye" ay ou dy ov dy V1-xye2

三、复合函数的中间变量既有一元又有多元函数的求导法则 定理 3 若（1）u x y  ( , )在点(x, y)处偏导数 存在，v y ( )在点 y 处可导 （2）函数 z f u v  ( , ) 在相应点(u,v) 处 具有连续的偏导数 , , z z u v     则复合函数 z f x y y  [ ( , ), ( )]   在点( , ) x y 处偏导 数 , z z x y     存在，且 z z u x u x         . z z u z dv y u y v dy             z  f u x y y v y 例 5 设 z uv  arcsin ，其中 2 , , y u xe v y   求 , z z x y     解：显然 2 2 2 2 , 1 1 z v z u u v u v u v         ， 所以 2 2 2 2 4 2 1 1 y y y z z u v y e e x u x u v x y e               , u u y y e xe x y       ， z z u z dv y u y v dy             2 2 2 2 2 1 1 v u y xe y u v u v       2 4 2 ( 2) 1 y y y xye x y e     z  f u x y y v y

复合函数的中间变量既有一元又有多元函数的求导法则 Ouou 例6设u=e2+,z=x2siny求 =2x(x+2z)e++: siny Ox'dy 解：令fx,y,)=e+,则 =2x(x+2x2siny)en sin y 又 f=2e+2+ f'=2xer2+2+2 =x'cosy f'=2zer++2 ay 所以 =2xsiny 告=+器 所以 0+盘 =2(y+zx2cosy)e =2xe+2e2xsiny =2(y+xsin ycos y)e

三、复合函数的中间变量既有一元又有多元函数的求导法则 例 6 设 2 2 2 x y z u e    ， 2 z x y  sin 求 , u u x y     解： 令 2 2 2 ( , , ) x y z f x y z e    ，则 x y z x y u f  2 2 2 2 x y x z f xe     2 2 2 2 x y z z f ze     2 sin x z x y    所以 x z u z f f x x          2 2 2 2 2 2 2 2 2 sin x y z x y z xe ze x y          2 2 2 2 2 in s x y z x x z e y       2 2 4 2 2 sin 2 2 sin sin x y x y x x x y y e     又 2 2 2 2 x y y z f ye     2 x y cos z y    y z u z f f y y          2 2 2 2 2 2 2 2 2 cos x y z x y z ye ze x y          2 2 2 2 2 cos x y z y zx y e       2 2 4 2 4 sin 2 sin cos x y x y y x y y e     所以

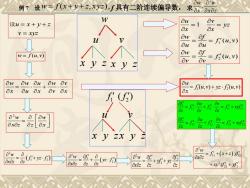
Ow d-w 例7设w=f(x+y+2,xy2),f具有二阶连续偏导数， 求axax2 设u=x十y+2 Ou=1 O a a .=y V=XVZ Ow= Ou 过=f(u,) 8 w=f(u,v) ow of Ov Ov =f乃(u,v) 8x Ou Ox Ov Ox wf(u)+(u) 2w Ow 8x82 =+0 d. w= w_+（f w_正++ =+(x+)形 +xyf妇+f5

w u v x y z x y z 例 7 设 w f x y z xyz    ( , ), f 具有二阶连续偏导数， 求 2 , w w x x z      u x y z v xyz     设 w f u v  ( , ) w w u w v x u x v x               1 2 1 ( , ) ( , ) u v yz x x w f f u v u u w f f u v v v                     1 2 ( , ) ( , ) w f u v yz f u v x        1 2 f f   ( ) u v x y zx y z 2 w w x z z x               2 1 2 w f yz f x z z             2 1 2 w f yz f x z z z             2 1 2 2 w f f yf yz x z z z             1 11 12 11 12 2 21 22 21 22 f u v f f f xyf z z z f u v f f f xyf z z z                                     2 11 12 2 22 2 w f x z yf x z xy zf yf           