南阳师范学院：《高等数学》课程教学资源（课件讲稿）第八章 多元函数微分法及其应用 第五节 隐函数的求导法则

§8.5隐函数的求导法则 一元隐 二元隐 函数的 函数的 求导法则 内容 求导法则

主 要 内 容 §8.5 隐函数的求导法则 一元隐 函数的 求导法则 二元隐 函数的 求导法则

一元隐函数的求导法则 观察 (1)x2+y2=1 隐函数存在定理1：若函数F(x,)在点(x,) (2)e*-xy2=0 的某一邻域内有连续的偏导数 且 F(x,%)=0F,'(xo,%)≠0 发现 (1)x2+y2=1可以确定一个函数 则方程F(x,)=0在点(x,)的某一邻域内唯 (2)e-y2=0可以确定一个函数 一确定一个可导函数y=f(x)且导函数连续 若由函数F(x,y)=0可以确定 将y=(x)代入F(x,y)=0 dy__ 因变量y与 dx 自变量x之间的函数关系 那么这种函数就叫做隐函数， @ 等式两边对x求导 但并非每一个方程都可以确定一个函数 F[x,f(x)]=0 +Ek .=0 如 x2+y2+1=0

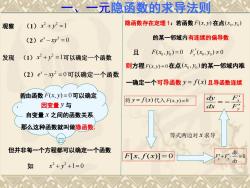
一、一元隐函数的求导法则 观察 （1） 2 2 x y  1 （2） 2 0 x e xy   发现 （1） 2 2 x y  1可以确定一个函数 （2） 2 0 x e xy   可以确定一个函数 但并非每一个方程都可以确定一个函数 如 2 2 x y   1 0 由函数 F x y ( , ) 0  可以确定 . 因变量 y 与 自变量 x 之间的函数关系 那么这种函数就叫做隐函数. 隐函数存在定理 1：若函数 F x y ( , ) 在点 0 0 ( , ) x y 的某一邻域内有连续的偏导数 且 0 0 F x y ( , ) 0  0 0 ( , ) 0 F x y y   则方程F x y ( , ) 0  在点 0 0 ( , ) x y 的某一邻域内唯 一确定一个可导函数 y f x  ( ) 且导函数连续 将 y f x  ( ) 代入 F x y ( , ) 0  F x f x [ , ( )] 0  等式两边对 x 求导 0 x y dy F F dx      x y dy F dx F     . 若

一元隐函数的求导法则 例1 求由方程x2+y2=1所确定的隐函数 法2：将x2+y2=1两边微分 y=f(x)的一阶导数与二阶导数 由于y=f(x)根据一元函数微分法则 法1：(1)确定函数F(x,y)的表达式 可得 2xdx+2ydy =0 (2)求F(x,y)对xy的偏导数F,F, 从而当y≠0时， dx y (3)代入公式：-化简求出导数 dx F 解：令F(xy)=x2+y2-1,则 F'=2x,F'=2y + 从而当y≠0时， y

一、一元隐函数的求导法则 例 1 求由方程 1 2 2 x  y  所确定的隐函数 y  f (x)的一阶导数与二阶导数 法 1：（1）确定函数 F x y ( , ) 的表达式 （2）求 F x y ( , ) 对 x y, 的偏导数 , F F x y   （3）代入公式 x y dy F dx F     化简求出导数 解：令 2 2 F x y x y ( , ) 1    ，则 F x F y x y     2 , 2 从而当 y  0时，x y dy x F dx F y       法 2：将 2 2 x y  1两边微分 由于 y f x  ( ) 根据一元函数微分法则 可得 2 2 0 xdx ydy   dy x dx y   从而当 y  0时， 2 2 d y d dy d x dx dx dx dx y                2 y xy y     2 x y x y y          2 2 3 y x y    3 1 y  

二元隐函数的求导法则 将z=f(x,y)代入F(x,y,z)=0 若因变量z与自变量x,y之间 的函数关系有F(x,y,)三0 所确定，这种函数就叫做隐函数. F[x,y,f(x,y)]=0 等式两边分别对 x,y求导 隐函数存在定理2：若函数F(x,y,)在点(x,,) F'+F'. =0 Ox 的某一邻域内有连续的偏导数 F+E 2二0 ay 且 F(x0,,0)=0,F'(xo,0,0)≠0 F≠0 则方程Fx,y,)=0在点(x,%,0)的某一邻 域内唯具有连续偏导数的函数z=∫(x,y) F

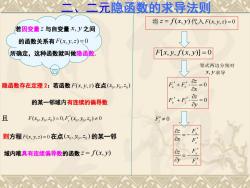
二、二元隐函数的求导法则 若因变量 z 与自变量 x y, 之间 的函数关系有 F x y z ( , , ) 0  所确定，这种函数就叫做隐函数. 隐函数存在定理 2：若函数 F x y z ( , , ) 在点 0 0 0 ( , , ) x y z 的某一邻域内有连续的偏导数 且 0 0 0 0 0 0 ( , , ) 0, ( , , ) 0 F x y z F x y z z    则方程F x y z ( , , ) 0  在点 0 0 0 ( , , ) x y z 的某一邻 域内唯具有连续偏导数的函数 z f x y  ( , ) 将 z f x y  ( , ) 代入F x y z ( , , ) 0  F x y f x y [ , , ( , )] 0  等式两边分别对 x y, 求导 0 0 x z y z z F F x z F F y               0 F z   x z y z z F x F z F y F            

二、二元隐函数的求导法则 例2由方程x2+y2+z2-4红=0确定 从雨当：2时产 2 z为x,y的函数，求x 票a){) 法1：(1)确定函数F(x,y,z)的表达式 (2-z)-x9 (2-) (2)求F(x,y,z)对x,y,z的偏导数 (2- EEE 2-z)+x 2-2 (2-)2 8代入公式容是容是化满 =(2-2)2+x2 (2-z)2 解：令F(xy,z)=x2+y2+z2-42,则 必做题：习题8-51,2,5,7,8 F'=2x,F,'=2y,F'=2z-4 选做题：习题8-53,4,6

二、二元隐函数的求导法则 例 2 由方程 2 2 2 x y z z     4 0 确定 z 为 x y, 的函数，求 2 2 z x   法 1：（1）确定函数 F x y z ( , , ) 的表达式 （2）求 F x y z ( , , ) 对 x y z , , 的偏导数 , , F F F x y z    （3）代入公式 , x y z z z z F F x y F F             化简 解：令 2 2 2 F x y z x y z z ( , , ) 4     ，则 2 , 2 , 2 4 F x F y F z x y z        从而当 z  2时， 2 x z z x F x F z         2 2 2 z z x x x x x z                          2 (2 ) 2 2 x z x z z         2 (2 ) (2 ) 2 z z x x z          2 2 2 (2 ) 2 z x z     必做题：习题 8-5 1，2，5，7，8 选做题：习题 8-5 3，4，6