新疆大学：《高等数学》课程教学资源（PPT课件）第1章 微积分的基础和研究对象 2.3 连续函数

第2章微积分的直接基础一函数 §2.1数列极限与函数极限 §2.2极限的性质与运算 §2.3连续函数

第2章微积分的直接基础——函数 §2.1 数列极限与函数极限 §2.2 极限的性质与运算 §2.3 连续函数

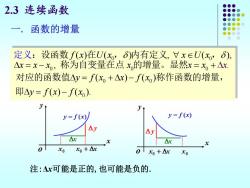
2.3连续函数 一.函数的增量 定义：设函数f(x)在U(x,δ)内有定义，Vx∈U(x,δ)， △x=x-x,称为自变量在点x的增量。显然x=x,+△x 对应的函数值△y=f(x,+△x)-f(x)称作函数的增量， 即△y=f(x)-f(xo). y=f(x) y=f(x) △ △y △ △( xo 0+△r 01x+△x 注：△x可能是正的，也可能是负的

2.3 连续函数 一. 函数的增量 0 0 0 0 0 ( ) ( ) , ( ), , . f x U x x U x x x x x x x x      = − = +  ：设函数 在 ， 内有定义 ， 称为自变量在点 的增 然 义 量。显 定 0 0 0 ( ) ( ) ( ) ( ). y f x x f x y f x f x  = +  −  = − 对应的函数值 称作函数的增量， 即 注:Δx可能是正的,也可能是负的

2.3连续函数 ,函数的增量 例如：求函数y=x2+1在x点的增量 给增量△x,x=x+△x, Ay=f(x+△x)-f(x)=(x+△x)2-x2 =2x△x+(△x)2 练习：求函数y=上在x,(X,≠0)点的增量

2.3 连续函数 一. 函数的增量 2 0 例如：求函数y x x = +1 . 在 点的增量 0 给增量 = +  x x x x ， , 2 2 0 0 0  = +  − = +  − y f x x f x x x x ( ) ( ) ( ) 2 0 =  +  2 ( ) x x x 0 0 1 y x x( 0) . x 练习：求函数 =  在 点的增量

2.3连续函数 二。 连续函数的定义 定义1设函数f(x)在U(x,δ)内有定义，如果 当自变量的增量△x趋向于O时，对应的函数 增量△y也趋向于0，即lim△y=0, △x>0 或lim[f(x+△x)f(x】=0,那么就称函数 0 f(x)在点x连续，也称x是f(x)连续点. 说明：1.连续函数的自变量变化很小时，函数值的变化也很小 2.图像上看，连续函数是一条连续而不间断的曲线

2.3 连续函数 0 0 0 0 0 0 0 ( , ) , 0 0 lim 0 lim[ ] 0 x x f x U x x y y f x x f x f x x x f x   →  →    = +  = 设函数（ ）在 内有定义 如果 当自变量的增量 趋向于 时，对应的函数 增量 也趋向于 ，即 ， 或 （ ）-（ ） ，那么就称函数 （ ）在点 连续 定义1 ，也称 是（ ）连续点. 二. 连续函数的定义 说明： 1. 连续函数的自变量变化很小时，函数值的变化也很小. 2.图像上看，连续函数是一条连续而不间断的曲线

2.3连续函数 连续函数的定义 定义2 设函数f(x)在U(x,δ)内有定义，如果 当x→x时，f(x)的极限存在且等于f(x),即 limf(x)=f(x),那么就称f(x)在点x,连续 说明：定义1与定义2是等价的， 定义1 lim Ay=0limf(x+Ax)-f(xa)=0 △x→0 台mf(化，+△e)=fx)台limf(x)=fx,) 定义2

2.3 连续函数 二. 连续函数的定义 0 0 0 0 0 0 ( ) ( , ) , ( ) ( ) lim ( ) ( ) ( ) . x x f x U x x x f x f x f x f x f x x  → → = 设函数 在 内有定义 如果 当 时， 的极限存在且 定 等于 ，即 ，那么就称 在点 2 连续 义 0 lim 0 x y  →  = 0 0 0 lim ( ) ( ) 0 x f x x f x  →  +  − =     说明： 定义1与定义2是等价的. 0 0 0 lim ( ) ( ) x f x x f x  →  +  = 0 0 lim ( ) ( ) x x f x f x →  = 定义1 定义2

2.3连续函数 二。连续函数的定义 例题 证明函数f(x)=1在定义域内连续 X 证法1.设x为f(x)的定义域X=(-oo,0)U(0,+o∞)内的 任一点，给定△x,使得x,+△x∈X,则 11 -△x △y= x+△xx0 (xo+Ax)xo ∴.lim△y=0,即f(x)在x连续 由x,任意性可知在f(x)=定义域内，f(x)是连续的

2.3 连续函数 0 0 0 0 0 0 1 1 = , ( ) lim 0, ( ) . x x y x x x x x x y f x x  → −   = − +  +    = 即 在 连续 1 f x( ) . x 证明函数 = 在定义域内连续 0 0 1. ( ) (- 0) (0 ) , , + , x f x X x x x X   +     证法 设 为 的定义域 = ， ， 内的 任一点 给定 使得 则 二. 连续函数的定义 例题 o x x y y 0 1 x f x f x ( ) ( ) x 由 任意性可知在 = 定义域内, 是连续的

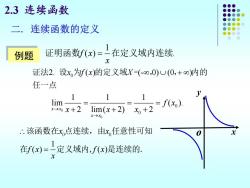
2.3连续函数 二 连续函数的定义 例题 证明函数f(x)=在定义域内连续 证法2.设x,为f(x)的定义域X=(-0,0)U(0,+o)内的 任一点 lim- xxx+2lim(x+2)x。+2 f】 .该函数在x点连续，由x,任意性可知 在f(x)=1定义域内，fx)是连续的

2.3 连续函数 0 0 1 ( ) ( ) x x f x f x x  = 该函数在 点连续，由 任意性可知 在 定义域内, 是连续的. 0 证法2. ( ) (- 0) (0 ) 设x f x X 为 的定义域 =   +  ， ， 内的 任一点 0 0 0 0 1 1 1 lim ( ). x x 2 lim( 2) 2 x x f x → x x x → = = = + + + x y 1 f x( ) . x 证明函数 = 在定义域内连续 二. 连续函数的定义 例题 o

2.3连续函数 三.函数的间断点 函数f(x)在点x处连续台lim=f(x) (I)f(x)在点x,处有定义； (2)imf(x)存在； x→x0 (3)lim f(x)=f() x→X0 如果上述三个条件中只要有一个不满足，则称 函数f(x)在点x处不连续（或间断），并称点x为 f(x)的不连续点（或间断点）

2.3 连续函数 三. 函数的间断点 0 0 , ( ) ( ), ( ) ( ). f x x x f x 如果上述三个条件中只要有一个不满足 则称 函数 在点 处不连续 或 并称点 为 的不连续点 或 间断 间断点 0 0 (3) lim ( ) ( ). x x f x f x → = 0 (2) lim ( ) ; x x f x → 存在 0 0 0 ( ) lim ( ) x x f x x f x → 函数 在点 处连续 = 0 (1) ( ) ; f x x 在点 处有定义

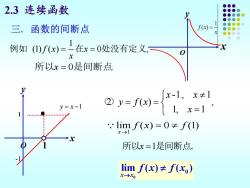
2.3连续函数 三.函数的间断点 (x 例如（①f()=上在x=0处没有定义， X 所以x=0是间断点 =x-1 == .:limf(x)=0≠f(1) 所以x=1是间断点. limf(x)≠f(x) x→x0

2.3 连续函数 -1, 1 2 ( ) , 1, 1 x x y f x x   = =   = （） 1 lim ( ) 0 (1) x f x f → =  所以x =1是间断点. 1 (1) ( ) 0 , f x x x 例如 = = 在 处没有定义 所以x = 0 . 是间断点 0 0 lim ( ) ( ) x x f x f x →  1 f x( ) x = y x O 三. 函数的间断点 x o y -1 1 1 y x = −1

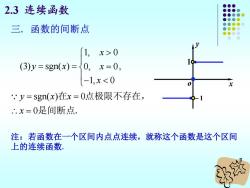
2.3连续函数 三.函数的间断点 1, x>0 (3)y=sgn(x)=0,x=0, -1,x<0 ,y=sgn(x)在x=0点极限不存在， .x=0是间断点. 注：若函数在一个区间内点点连续，就称这个函数是这个区间 上的连续函数

2.3 连续函数 1, 0 (3) sgn( ) , 0, 0 1, 0 x y x x x    = =  =   −  sgn( ) 0 0 y x x x = =  = 在 点极限不存在， 是间断点. 注：若函数在一个区间内点点连续，就称这个函数是这个区间 上的连续函数. 三. 函数的间断点 y x 1 − 1 o