《水力学》课程教学资源(PPT课件)第三章 水动力学基础

第三章水动力学基础第一节描述液体运动的两种方法一、拉格朗日方法(LagrangianMethod)是以流场中每一流体质点作为描述对象的方法,它以流体个别质点随时间的运动为基础,通过综合足够多的质点(即质点系)运动求得整个流动。一一一一质点系法。即跟随质点研究质点运动参数的变化。[x= x(a,b,c,t)空间坐标y=y(a,b,c,t)z = z(a,b,c,t)(a.b,c)为t-t.起始时刻质点所在的空间位置坐标,称为拉格朗日数。所以,任何质点在空间的位置(xyz)都可看作是(a.b.c)和时间t的函数(1)(a,b,c)=Const,t为变数,可以得出某个指定质点在任意时刻所处的位置。(2)(a.b.c)为变数.t=Const,可以得出某一瞬间不同质点在空间的分布情况,返回书目返回课目U
1 1 第三章 水动力学基础 第一节 描述液体运动的两种方法 一、拉格朗日方法(Lagrangian Method) 是以流场中每一流体质点作为描述对象的方法,它以流体个别质 点随时间的运动为基础,通过综合足够多的质点(即质点系)运动求 得整个流动。-质点系法。即跟随质点研究质点运动参数的变化。 (a,b,c)为t=t0起始时刻质点所在的空间位置坐标,称为拉格朗日数。所以,任何 质点在空间的位置(x,y,z)都可看作是(a,b,c)和时间t的函数 空间坐标 = = = ( , , , ) ( , , , ) ( , , , ) z z a b c t y y a b c t x x a b c t (1) (a,b,c)=Const , t为变数,可以得出某个指定质点在任意时刻所处的位置。 (2) (a,b,c)为变数, t =Const ,可以得出某一瞬间不同质点在空间的分布情况

由于位置又是时间t的函数,对流速求导可得加速度:ux速度uyu,绿像aux02xaOt2Otauy2y加速度aOtOt2Ou-022a.Ot2Ot由于流体质点的运动轨迹非常复杂,而实用上也无须知道个别质点的运动情况,所以除了少数情况(如波浪运动)外,在工程流体力学中很少采用。返回课目返回书目U
2 2 由于位置又是时间 t 的函数,对流速求导可得加速度: 由于流体质点的运动轨迹非常复杂,而实用上也无须知道个别质点的运动情况, 所以除了少数情况(如波浪运动)外,在工程流体力学中很少采用。 速度 = = = t z u t y u t x u z y x 加速度 = = = = = = 2 2 z z 2 2 y y 2 2 x x t z t u a t y t u a t x t u a

二、欧拉法(Euler Method)是以流体质点流经流场中各空间点的运动即以流场作为描述对象研究流动的方法。一一流场法像之它不直接追究质点的运动过程,而是以充满运动液体质点的空间一流场为对象。研究各时刻质点在流场中的变化规律。将个别流体质点运动过程置之不理,而固守于流场各空间点。通过观察在流动空间中的每个空间点上运动要素随时间的变化,把足够多的空间点综合起来而得出的整个流体的运动情况。流场运动要素是时空(x,y,Z,t)的连续函数:u, =u,(x,y,z,t)(x,y,Z,t)一欧拉变量速度u, =u,(x,y,z,t)[u, =u.(x, y,z,t)因欧拉法较简便,是常用的方法。返回课目返回书目u
3 3 二、欧拉法(Euler Method) 是以流体质点流经流场中各空间点的运动即以流场作为描述对象研 究流动的方法。——流场法 它不直接追究质点的运动过程,而是以充满运动液体质点的空间——流场为对 象。研究各时刻质点在流场中的变化规律。将个别流体质点运动过程置之不理,而 固守于流场各空间点。通过观察在流动空间中的每一个空间点上运动要素随时间的 变化,把足够多的空间点综合起来而得出的整个流体的运动情况。 流场运动要素是时空(x,y,z,t)的连续函数: = = = ( , , , ) ( , , , ) ( , , , ) u u x y z t u u x y z t u u x y z t z z y y x x 速度 (x,y,z,t)——欧拉变量 因欧拉法较简便,是常用的方法
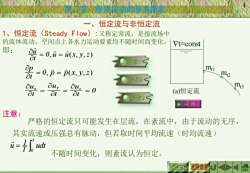
第二节液体运动的基本概念、恒定流与非恒定流1恒定流(SteadyFlow):又称定常流,是指流场中的流体流动,空间点上各水力运动要素均不随时间而变化。Vt=const即:Qui= 0,u=i(x,y,z)at永假damt1= 0,p= p(x, y,z)m2茅像之mt3auyOuxou=0(a)恒定流tatat永像动画注意:严格的恒定流只可能发生在层流,在紊流中,由于流动的无序,其实流速或压强总有脉动,但若取时间平均流速(时均流速)i=+uudt不随时间变化,则紊流认为恒定。返回书目返回课目U
4 4 第二节 液体运动的基本概念 1、恒定流(Steady Flow):又称定常流,是指流场中 的流体流动,空间点上各水力运动要素均不随时间而变化。 即: 0, u u(x, y, z) t u = = 0 t u t u t ux y z = = = 0, p p(x, y, z) t p = = 一、恒定流与非恒定流 注意: t=const mt1 mt2 mt3 (a)恒定流 = T 0 udt T 1 u 严格的恒定流只可能发生在层流,在紊流中,由于流动的无序, 其实流速或压强总有脉动,但若取时间平均流速(时均流速) 不随时间变化,则紊流认为恒定

2、非恒定流(UnsteadyFlow)又称非定常流,是指流场中的流体流动空间点上各水力运动要素只要有任何一个随时间的变化而变化的流动。Vt1Vt2即:aVt3±0,u=ü(x,y,z,t)mtl永像流线+ 0, p = p(x, y,z,t)m(b)非恒定流2im迹线ouyau_三者中至少一个Ouxat 2at2at 不等于0。永注意:在非恒定流情况下,流线的位置随时间而变:流线与迹线不重合。在恒定流情况下,流线的位置不随时间而变,且与迹线重合。返回书目返回课目U
5 5 在非恒定流情况下,流线的位置随时间而变;流线与迹线不重合。 在恒定流情况下,流线的位置不随时间而变,且与迹线重合。 注意: 0, u u(x, y, z,t) t u = 0, p p(x, y, z,t) t p = 2、非恒定流(Unsteady Flow) 又称非定常流,是指流场中的流体流动空间点上各水力 运动要素只要有任何一个随时间的变化而变化的流动。 即: t u t u t ux y z , , 三者中至少一个 不等于0。 流线 迹线 t1 mt1 mt2 mt3 t3 t2 (b)非恒定流

二、迹线与流线1、流线流线(StreamLine)是表示某一瞬时流体各点流动趋势的曲线,曲线上任一点的切线方向与该点的流速方向重合。最像流谱流线Flow Spectrum And Streamline返回课目返回书目
6 6 显示图片 二、迹线与流线 1、流线 流线(Stream Line)是表 示某一瞬时流体各点流动趋 势的曲线,曲线上任一点的 切线方向与该点的流速方向 重合

流线流线的作法:在流场中任取一点(如图),绘出某时刻通过该点的流体质点的流uu4U速失量u,再画出距1点很近的2点在同一时刻通过该处的流体质点的流速失量.…,如此继续下去,得一折线1234·,若各点无限接近,其极限就是某时刻的流线。流线是欧拉法分析流动的重要概念。返回课目返回书目U
7 7 1、流线 流线的作法: 在流场中任取一点(如图),绘 出某时刻通过该点的流体质点的流 速矢量u1,再画出距1点很近的2点 在同一时刻通过该处的流体质点的 流速矢量u2. .,如此继续下去, 得一折线1234 . .,若各点无限 接近,其极限就是某时刻的流线。 流线是欧拉法分析流动的重要概念。 1 2 3 4 u2 u1 u3 u4
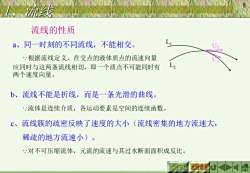
流线流线的性质La、同一时刻的不同流线,不能相交。:根据流线定义,在交点的液体质点的流速向量W应同时与这两条流线相切,即一个质点不可能同时有两个速度向量。b、流线不能是折线,而是一条光滑的曲线。流体是连续介质,各运动要素是空间的连续函数。C、流线簇的疏密反映了速度的大小(流线密集的地方流速大稀疏的地方流速小)。·对不可压缩流体,元流的流速与其过水断面面积成反比。返回书目返回课目U
8 8 流线的性质 a、同一时刻的不同流线,不能相交。 根据流线定义,在交点的液体质点的流速向量 应同时与这两条流线相切,即一个质点不可能同时有 两个速度向量。 b、流线不能是折线,而是一条光滑的曲线。 流体是连续介质,各运动要素是空间的连续函数。 c、流线簇的疏密反映了速度的大小(流线密集的地方流速大, 稀疏的地方流速小)。 对不可压缩流体,元流的流速与其过水断面面积成反比。 1、流线 U2 L1 L2 U1

2.迹线2、迹线迹线(PathLine)是指某一质点在某一时段内的运动轨迹线。永像#像2返回课目返回书目U
9 9 显示图片 2.迹线 迹线(Path Line)是指某一 质点在某一时段内的运动轨迹 线。 2、迹线

流线迹线色线义备概念名定注流线流线方程为:流线是表示流体流动趋势的一条dx-dy-dz曲线,在同一瞬时线上各质点的速度uuyu.向量都与其相切,它描述了流场中不式中时间t为参变量。同质点在同一时刻的运动情况。迹线迹线是指某一质点在某一时刻内迹线方程为:dxdy_dz5=dt的运动轨迹,它描述流场中同一质点2uuu在不同时刻的运动情况。式中时间t为自变量。脉线恒定流中,流线、迹线、脉线(色线)是指源于一点的很脉线三线重合。多流体质点在同一瞬时的连线。例题例题2例题3返回课目返回书目
10 10 概念名 定 义 备 注 流 线 流线是表示流体流动趋势的一条 曲线,在同一瞬时线上各质点的速度 向量都与其相切,它描述了流场中不 同质点在同一时刻的运动情况。 流线方程为: d x u d y u d z x y uz = = 式中时间 t 为参变量。 迹 线 迹线是指某一质点在某一时刻内 的运动轨迹,它描述流场中同一质点 在不同时刻的运动情况。 迹线方程为: d x u d y u d z u d t x y z = = = 式中时间 t 为自变量。 脉 线 脉线(色线)是指源于一点的很 多流体质点在同一瞬时的连线。 恒定流中,流线、迹线、 脉线三线重合。 流线、迹线、色线
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《水力学》课程教学资源(PPT课件)第一章 绪论.ppt
- 《水力学》课程教学资源(PPT课件)第四章 液流形态及水头损失.ppt
- 《水力学》课程实验教学指导书(共十五个实验).doc
- 《水力学》课程授课教案.doc
- 《水力学》课程教学大纲 Hydraulics(给排专业).doc
- 《水力学》课程教学大纲 Hydraulics(土木专业).doc
- 《水力学》课程教学大纲 Hydraulics(环工专业).doc
- 《水力学》课程教学大纲 Hydraulics(农水专业).doc
- 《病理生理学》课程教学课件(PPT讲稿)第一章 绪论 Pathophysiology、第二章 疾病概论.ppt
- 《病理生理学》课程教学课件(PPT讲稿)第三章 缺氧 Hypoxia.ppt
- 《病理生理学》课程教学课件(PPT讲稿)第四章 酸碱平衡和酸碱平衡紊乱(Acid-base balance and acid-base disturbance).ppt
- 《病理生理学》课程教学课件(PPT讲稿)第六章 缺血-再灌注损伤(ischemia-reperfusion injury).ppt
- 《病理生理学》课程教学课件(PPT讲稿)第七章 细胞凋亡与疾病.ppt
- 《病理生理学》课程教学课件(PPT讲稿)第八章 弥散性血管内凝血(Disseminated or diffuse intravascular coagulation,DIC).ppt
- 《病理生理学》课程教学课件(PPT讲稿)第九章 应激(stress).ppt
- 《病理生理学》课程教学课件(PPT讲稿)第十章 休克 Shock.ppt
- 《病理生理学》课程教学课件(PPT讲稿)第十一章 心功能不全(心力衰竭 Heart failure).ppt
- 《病理生理学》课程教学课件(PPT讲稿)第十二章 肝功能不全 Hepatic Insufficiency.ppt
- 《病理生理学》课程教学课件(PPT讲稿)第十三章 呼吸功能不全(respiratory failure).ppt
- 《病理生理学》课程教学课件(PPT讲稿)第十四章 多器官功能衰竭(multiple system organ failure,MSOF).ppt
- 《水力学》课程教学资源(PPT课件)第五章 有压管道中的恒定流.ppt
- 《水力学》课程教学资源(PPT课件)第二章 水静力学.ppt
- 《水力学》课程教学资源(PPT课件)第十三章 渗流.ppt
- 《水力学》课程教学资源(PPT课件)第六章 明渠恒定均匀流.ppt
- 《水力学》课程教学资源(PPT课件)第八章 堰流和闸孔出流.ppt
- 《水力学》课程教学资源(PPT课件)第七章 明渠恒定非均匀流.ppt
- 《给水排水管网系统》课程教学大纲 Water and Wastewater Pipeline Network.doc
- 《给水排水管网系统》课程授课教案(讲稿,华北理工大学:刘晓).doc
- 《给水排水管网系统》课程教学课件(PPT讲稿)第11章 给水排水管网管理与维护.pps
- 《给水排水管网系统》课程教学课件(PPT讲稿)第10章 给水排水管道材料和附件.pps
- 《给水排水管网系统》课程教学课件(PPT讲稿)第9章 雨水管网设计和计算.pps
- 《给水排水管网系统》课程教学课件(PPT讲稿)第8章 污水管网设计与计算.pps
- 《给水排水管网系统》课程教学课件(讲稿)第7章 给水管网运行与调度.pdf
- 《给水排水管网系统》课程教学课件(讲稿)第5章 给水管网水力分析.pdf
- 《给水排水管网系统》课程教学课件(PPT讲稿)第6章 给水管网工程设计.pps
- 《给水排水管网系统》课程教学课件(讲稿)第4章 给水排水管网模型.pdf
- 《给水排水管网系统》课程教学课件(PPT讲稿)第3章 给水排水管网水力学基础.pps
- 《给水排水管网系统》课程教学课件(PPT讲稿)第1章 给水排水管网系统概论 Water and Wastewater Pipeline Network.ppt
- 《给水排水管网系统》课程教学课件(PPT讲稿)第2章-给水排水管网工程规划.pps
- 《工程流体力学》课程教学大纲 engineering fluid mechanics.doc
