南京大学：《并行处理技术——分布式与并行计算 Distributed and Parallel computing（并行计算——结构、算法、编程）》课程教学资源（课件讲稿）第九章 并行数值算法（稠密矩阵运算）

第九章稠密矩阵运算 9.1矩阵的划分 92矩阵转置 93矩阵-向量乘法 9.4矩阵乘法

第九章 稠密矩阵运算 9.1 矩阵的划分 9.2 矩阵转置 9.3 矩阵 ‐向量乘法 9.4 矩阵乘法

9.1矩阵的划分 9.1.1带状划分 9.1.2棋盘划分

9.1 矩阵的划分 9.1.1 带状划分 9.1.2 棋盘划分

带状划分 *16X16阶矩阵，p=4 Po P1 P2 P3 0 4 8 Po 12 1 5 9 P1 13 0123456789101112131415 2 6 10 P2 14 3 7 11 P3 15 (a) (b) 列块带状划分 图9.1行循环带状划分 2011/11/15 5

带状划分  16×16阶矩阵，p=4 列块带状划分 行循环带状划分 PPPP 0 4 8 12 1 5 9 13 2 6 10 14 3 7 11 15 P P P P ( a ) ( b ) 图9.1 0123 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 5 2011/11/15

带状划分 *示例：p=3,27X27矩阵的3种带状划分 ■P2 ■P3 (a)block (b)cyclic (c)block-cyclic Striped row-major mapping of a 27 X 27 matrix on p=3 processors. 2011/11/15 6

带状划分  示例：p＝3，27× 27矩阵的3种带状划分 6 2011/11/15

9.1矩阵的划分 9.1.1带状划分 9.1.2棋盘划分

9.1 矩阵的划分 9.1.1 带状划分 9.1.2 棋盘划分

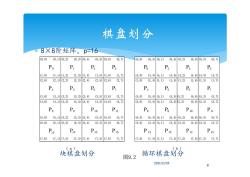
棋盘划分 *8X8阶矩阵，p=16 (0,0) (0,1)(0,2) (0,3)(0,4) (0,5)(0,6) (0,7) (0,0) (0,4)(0,1)(0,5)(0,2) (0,6)(0,3) (0,7) Po P P2 P3 Po P P2 P3 (1,0) (1,1)(1,2) (1,3)1,40 (1,5)(1,6) (1,7) (4,0) (4,4)(4,1) (4,5)(4,2) (4,6)(4,3) (4,7) (2,0) (2,1)(2,2) (2,3)(2,40 (2.5)(2,6) (2,7) (1.0) (1,4)(1,1) (1,5)(1,2) (1,6)(1,3) (1,7) P Ps Pe P P P P P (3,0) (3,1)(3,2) (3,3)3,40 (3,5)(3,6) (3,7) (5,0) (5,4)(5,1) (5,5)K5,2) (5,6)(5,3) (5,7) (4,0) (4,1)4,2) (4,3)(4,4) (4,5)(4,6) (4,7) (2,0) (2,40(2,1) (2,5)K2,2) (2,6)(2,3) (2,7) Ps Ps P10 Pu Ps P P10 Pu (5,0) (5,1)(5,2) (5,3)(5,4) (5,5)(5,6) (5,7) (6,0) (6,4)(6,1) (6,5)(6,2) (6,6)(6,3) (6,7) (6,0) (6,1)(6,2) (6,3)(6,4) (6,5)(6,6) (6,7) (3,0) (3,4)(3,1) (3,5)(3,2) (3,6)(3,3) (3,7) P12 P13 P14 P15 P12 P13 P14 P15 (7,0) (7,107,2) (7,3)(7,40 (7,5)(7,6) (7,7) (7,0) (7,47,1) (7,5(7,2) (7,67,3) (7,7) a 块棋盘划分 图9.2 循环棋盘划分 2011/11/15 8

棋盘划分  8×8阶矩阵，p=16 块棋盘划分 循环棋盘划分 ( a ) ( b ) 图9.2 6 10 14 7 11 15 4 8 12 5 9 13 6 10 14 (0,0) (1,0) (2,0) (3,0) (5,0) (4,0) (7,0) (6,0) (0,1) (1,1) (2,1) (3,1) (5,1) (4,1) (7,1) (6,1) (0,2) (1,2) (2,2) (3,2) (5,2) (4,2) (7,2) (6,2) (0,3) (1,3) (0,4) (1,4) (2,3) (3,3) (2,4) (3,4) (5,3) (4,3) (5,4) (4,4) (7,3) (6,3) (7,4) (6,4) (0,5) (1,5) (0,6) (1,6) (2,5) (3,5) (2,6) (3,6) (5,5) (4,5) (5,6) (4,6) (7,5) (6,5) (7,6) (6,6) (0,7) (1,7) (2,7) (3,7) (5,7) (4,7) (7,7) (6,7) (0,0) (2,0) (3,0) (5,0) (4,0) (7,0) (6,0) (1,0) (6,1) (1,1) (0,4) (1,4) (2,1) (3,1) (2,4) (3,4) (5,1) (4,1) (5,4) (4,4) (7,4) (7,1) (6,4) (0,1) (1,2) (0,5) (1,5) (2,2) (3,2) (2,5) (3,5) (5,2) (4,2) (5,5) (4,5) (7,2) (6,2) (7,5) (6,5) (0,2) (1,3) (0,6) (1,6) (2,6) (2,3) (3,6) (5,3) (4,3) (5,6) (4,6) (7,3) (6,3) (7,6) (6,6) (0,3) (3,3) (0,7) (1,7) (2,7) (3,7) (5,7) (4,7) (7,7) (6,7) 3 7 11 15 0 4 8 12 1 5 9 13 23 012 8 2011/11/15

棋盘划分 *示例：p=4,16X16矩阵的3种棋盘划分 ■P2 3 1P4 (a)block (b)cyclic (c)block cyclic Checkerboard mapping of a 16 x 16 matrix on p=2 x 2 processors. 2011/11/15 9

棋盘划分  示例：p＝4，16×16矩阵的3种棋盘划分 9 2011/11/15

第九章稠密矩阵运算 9.1矩阵的划分 9.2矩阵转置 93矩阵-向量乘法 9.4矩阵乘法

第九章 稠密矩阵运算 9.1 矩阵的划分 9.2 矩阵转置 9.3 矩阵 ‐向量乘法 9.4 矩阵乘法

单处理机上的矩阵转置算法 算法91单处理机上的矩阵转置算法 输入：Anxn * 输出：AT Xn Begin for i=2 to n do for j=1 to i-1 do ai,j→aj,d endfor endfor End 运行时间：(n2-n)/2=0(n2) 11 2011/11/15

 算法9.1 单处理机上的矩阵转置算法  输入：ܣ௡ൈ௡  输出：ܣ௡்ൈ௡ Begin for i=2 to n do for j=1 to i‐1 do ܽ௜,௝ ՞ ܽ௝,௜ endfor endfor End 运行时间：ሺ݊ଶെ݊ሻ/2 ൌ ܱሺ݊ଶሻ 11 2011/11/15 单处理机上的矩阵转置算法

92矩阵转置 9.2.1棋盘划分的矩阵转置 92.2带状划分的矩阵转置

9.2 矩阵转置 9.2.1 棋盘划分的矩阵转置 9.2.2 带状划分的矩阵转置