新疆大学：《电子线路》课程教学课件（PPT讲稿，线性部分）第三章 场效应管 第三节 场效应管应用原理

第三节 场效应管应用

第三节 场效应管应用

一、有源电阻 与普通的线性电阻不同，用三端器件构成的有源电阻， 一般都是非线性的。 例如、有一三端器件(N沟道EMOS管)，连接成二端 有源电阻器，如图所示：

一、有源电阻 与普通的线性电阻不同，用三端器件构成的有源电阻， 一般都是非线性的。 例如、有一三端器件（N沟道EMOS管），连接成二端 有源电阻器，如图所示： iD S G D vDS R i v

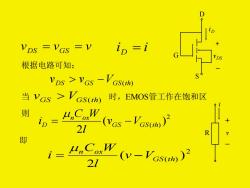
VDS VGS =v 根据电路可知： VDS YGs -VGs(th) 当vGs>Vcsh 时，EMOS管工作在饱和区 则 21 即 -Ys足 21

v v v DS = GS = i i D = iD S G D vDS 根据电路可知： DS GS VGS(t h) v  v − 当 vGS  VGS(t h) 时，EMOS管工作在饱和区 则 2 ( ) ( ) 2 G S G S t h n o x D v V l C W i = −  即 2 ( ) ( ) 2 GS t h n ox v V l C W i = −  R i v

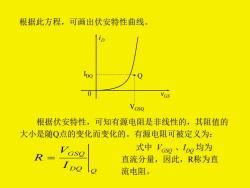
根据此方程，可画出伏安特性曲线。 VGS VGSQ 根据伏安特性，可知有源电阻是非线性的，其阻值的 大小是随Q点的变化而变化的。有源电阻可被定义为： 式中Vcso、lo均为 R 直流分量，因此，R称为直 流电阻

根据此方程，可画出伏安特性曲线。 0 iD vGS IDQ Q VGSQ 根据伏安特性，可知有源电阻是非线性的，其阻值的 大小是随Q点的变化而变化的。有源电阻可被定义为： DQ Q GSQ I V R = 式中 VGSQ 、IDQ 均为 直流分量，因此，R称为直 流电阻

V GSQ VGS 若在直流量上叠加一很小的交流量，如图所示： r= △E r为有源电阻器的交 流电阻，其阻值的大小是 △VGs Q点处切线斜率的倒数。 VGS

IDQ Q VGSQ 0 iD vGS 若在直流量上叠加一很小的交流量，如图所示： D Q GS I V r   = r 为有源电阻器的交 流电阻，其阻值的大小是 Q点处切线斜率的倒数。 0 vGS iD I Q DQ VGSQ ΔVGS ΔID

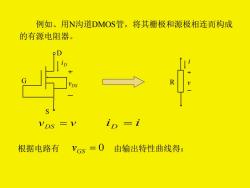
例如、用N沟道DMOS管，将其栅极和源极相连而构成 的有源电阻器。 VDS -V 根据电路有 VGS =0 由输出特性曲线得：

例如、用N沟道DMOS管，将其栅极和源极相连而构成 的有源电阻器。 S G D iD vDS i R v vDS = v i D = i 根据电路有 vGS = 0 由输出特性曲线得：

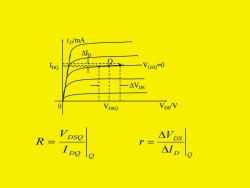
ip/mA VGso-0 △VDs VpsQ Vps/V R Vpse r= △VDs △ID

iD/mA VDS/V VGSQ=0 Q 0 IDQ VDSQ ΔID ΔVDS Q DQ DSQ I V R = D Q DS I V r   =

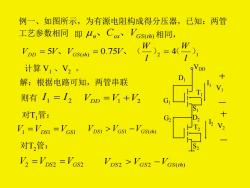
例一、如图所示，为有源电阻构成得分压器，已知：两管 工艺参数相同即4 Cox VGs(th)相同， Vo0=5弧、ex-0.75弘、（巴2。=4巴， 计算V,、V2。 解：根据电路可知，两管串联 D V 则有I1=I2VDD=V+V2 对T管： VI=VDST =VGST VDst VGsI -VGSu 2N2 对T,管： S V2 VDS2 =VGS2 VDS2 VGS2-VGS(h)

例一、如图所示，为有源电阻构成得分压器，已知：两管 工艺参数相同 即  n 、Cox、VGS(t h) 相同， ( ) 75 2 4 1 5 、 0. 、（ ） （ ） l W l W VD D = V VG S t h = V = 计算 V1 、V2 。 D2 G1 D1 T2 T1 S1 G2 S2 VDD I2 I1 V2 V1 解：根据电路可知，两管串联 则有 1 2 I = I VDD =V1 +V2 对T1管： V1 =VDS1 =VGS1 VDS1  VGS1 −VGS(t h) 对T2管： V2 =VDS2 =VGS2 VDS 2  VGS 2 −VGS(t h)

两管均工作在饱和区： 则有 1,=1n=4-(g-VP 21 1=1m=%化-aw 2l2 -S-ran>=么-S5化-aaw月 2l1 212 gW-asy=要-w了

两管均工作在饱和区： 则有 2 1 ( ) 1 1 1 1 ( ) 2 GS t h n o x D V V l C W I = I = −  2 2 ( ) 2 2 2 2 ( ) 2 GS t h n o x D V V l C W I = I = −  − = 2 1 ( ) 1 1 ( ) 2 GS t h n ox V V l  C W 2 2 ( ) 2 2 ( ) 2 GS t h n ox V V l C W −  − = 2 1 ( ) 1 1 ( ) V VGS t h l W 2 2 ( ) 2 2 ( ) V VGS t h l W −

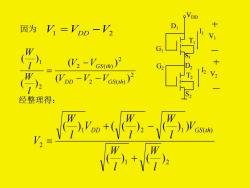
因为V=VDD-V2 D (W2-'cs)2 (Vpp-V2-Vosuh)2 经整理得： w+-g +

因为 V1 = VDD − V2 2 2 ( ) 2 2 ( ) 21 ( ) ( ) ( ) ( ) DD GS t h GS t h V V V V V lWlW − − − = 经整理得： 1 2 1 2 1 ( ) 2 ( ) ( ) ( ) ( ( ) ( ) ) lW lW V lW lW V lW V D D G S t h + + − = D 2 G 1 D 1 T 2T 1 S 1 G 2 S 2VDD I 2 I 1 V 2 V 1