珠海科技学院：《数字信号处理》课程教学资源（习题讲解）第一章

第一章习题讲解 2024/10/21

第一章习题讲解 2024/10/21 1

1-2已知线性移不变系统的输入为x(n),系统的 单位抽样响应为h(n),试求系统的输出y(n), 并画图。 2)x(n)=R (n),h(n)=R,(n) 0 解： (u)y 0 0 1 0 99 y(n)=x(n)*h(n)=R(n)*R (n) [8(n)+(n-1)+8(n-2)]*R(n） =R,(n)+R(n-1)+R,(n-2） 2024/10/21

解： 2） ， x n R n h n R n ( ) = = 3 4 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3 4 y n x n h n R n R n =  =  1-2 已知线性移不变系统的输入为 ，系统的 单位抽样响应为 ，试求系统的输出 ， 并画图。 x n( ) h n( ) y n( ) = + − + −       (n n n R n ) ( 1 2 ) ( ) 4 ( )   = + − + − R n R n R n 4 4 4 ( ) ( 1 2 ) ( ) 2024/10/21 2

3)x(n)=δ(n-2),h(n)=0.5"(n） 2 解： y(n）)=x(n)*h(n) =δ(n-2)*0.5R(n） =0.5"-2R(n-2) 0 0 2024/10/21

解： 3 2 0.5 ( ) ( ) ( ) 3 ( ) n ） ， x n n h n R n = − =  ( ) ( ) ( ) ( ) ( ) ( ) 3 2 3 2 0.5 0.5 2 n n y n x n h n n R n R n  − =  = −  = − 2024/10/21 3

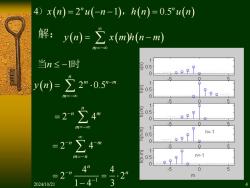
4)x(n）=2"u(-n-l),h(n)=0.5”u(n） 解：y(m)=∑x(mh(a-m） 当n≤-l时 05 y(m）=∑2”.0.5-w 5 0 目0.5 m=-00 0 9p. 0 =2"∑4 05 5 7 05 n=.1 =2∑4 7 m=-n 05 n1 4" 4 -5 0 5 =2” on m 2024/10/21 1-4- 3

解： ( ) ( ) ( ) m y n x m h n m  =− = −  4 2 1 0.5 ( ) ( ) ( ) ( ) n n ） ， x n u n h n u n = − − = 当 时 n  −1 ( ) 2 0.5 n m n m m y n − =− =   2 4 n n m m − =− =  2 4 n m m n  − − = − =  1 4 4 2 2 1 4 3 n −n n − = =  2024/10/21 − 4

当n≥0时 =∑2”05 (u)y 05 99 n1=-0 7 0.5 -2∑4 0 5 n1 m=-00 0 1 00 n>.1 =2-】 4 5 0 m=1 08 =21 0 ）-32”a(-n-）+32(o） 2024/10/2

当 时 n  0 ( ) 1 2 0.5 m n m m y n − − =− =   ( ) ( ) ( ) 4 1 2 1 2 3 3 n n y n u n u n −  =  − − +  1 2 4 n m m − − =− =  1 2 4 n m m  − − = =  1 1 4 1 2 2 1 4 3 n n − − − − = =  − 2024/10/21 5

1-3已知h(n)=a"u(-n-1),0<a<1,通过直 接计算卷积和的办法，试确定单位抽样响 应为h()的线性移不变系统的阶跃响应。 2024/10/21 6

( ) ( 1 0 1 ) n h n a u n a − = − −   ， h n( ) 1-3 已知 ，通过直 接计算卷积和的办法，试确定单位抽样响 应为 的线性移不变系统的阶跃响应。 2024/10/21 6

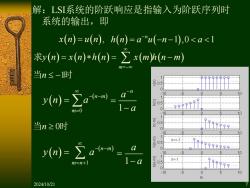
解：LSI系统的阶跃响应是指输入为阶跃序列时 系统的输出，即 x(n)=u(n),h(n=a"u(-n-1),0.1 -10 10 m 2024/10/21

解：LSI系统的阶跃响应是指输入为阶跃序列时 系统的输出，即 ( ) ( 1 ,0 1 ) n h n a u n a − x n u n ( ) = ( ), = − −   ( ) ( ) ( ) ( ) ( ) m y n x n h n x m h n m  =− 求 =  = −  当 时 n  −1 当 时 n  0 ( ) ( ) 0 n m m y n a  − − = =  1 n a a − = − ( ) ( ) 1 n m m n y n a  − − = + =  1 a a = − 2024/10/21 7

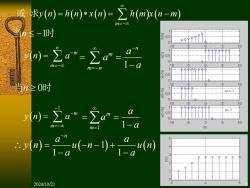
或 求y(n)=h(n)*x(n)=∑h(mr(n-m） -时 05 05 10 当20时 n<=1 Es× 0.5 -a 10 10 2024/10/21

或 当 时 n  −1 当 时 n  0 ( ) ( 1) ( ) 1 1 n a a y n u n u n a a −  = − − + − − ( ) ( ) ( ) ( ) ( ) m y n h n x n h m x n m  =− 求 =  = −  ( ) n m m y n a − =− =  1 n m m n a a a  − = − = = −  ( ) 1 m m y n a − − =− =  1 1 m m a a a  = = = −  2024/10/21 8

4判断下列每个序列是否是周期性的，若是周期 性的，试确定其周期 0o=4r7n司 解：x)为正弦序列其中= 3π 2元_14 是有理数 00 3 N=14是满足x(n+N)=x(n)的最小正整数 ∴x(n)为周期序列，周期为14 2024/10/21 9

1-4 判断下列每个序列是否是周期性的，若是周期 性的，试确定其周期 ( ) 3 1 cos 7 8 x n A n     = −     （ ） 0 3 7  其中 = 0 2 14 3   = 是有理数 解： 为正弦序列 x n( ) x n( )为周期序列，周期为14 N x n N x n = + = 14 ( ) ( ) 是满足 的最小正整数 2024/10/21 9

1-6试判断y(n)=[x(n)是否是线性系统？ 并判断是否是移不变系统？ 解：设T[x(m]-[x(n)T[x,(n-[x,(n :T[x(m)+x(n]=[x()+(m) =[x(m)+[x,(m)]+2x(n)x(n) ≠T[x(n)]+T[x,(n)]不满足可加性 或T[(m]-[ax(n)=a[x(n≠ar[x(] 不满足比例性 .不是线性系统 T[x(n-m)]=[x(n-m)=y(n-m)=[x(n-m)] 成悬移不变系统 10

1-6 试判断 是否是线性系统？ 并判断是否是移不变系统？ ( ) ( ) 2 y n x n =     ( ) ( ) ( ) ( ) 2 T x n x n x n x n     1 2 1 2 + = +     不满足可加性 或 ( ) ( ) 2 T ax n ax n     =     不满足比例性  不是线性系统 ( ) ( ) 2 T x n m x n m     − = −      是移不变系统 ( ) ( ) ( ) ( ) 2 2 = + +     x n x n x n x n 1 2 1 2 2      + T x n T x n     1 2 ( ) ( )     解：设     2 1 1 T x n x n ( ) ( ) =     2 2 2 T x n x n ( ) ( ) = ( ) ( ) 2 2 =  a x n aT x n         ( )   2 = y n m x n m − = − ( ) 2024/10/21 10