西安电子科技大学：《电路分析基础》课程教学资源（PPT课件）第五章 电路的频率响应和谐振现象（2/4）5.2 一阶电路和二阶电路的频率响应 5.3 串联谐振电路

知识点回顾 1.什么是网络函数（传输函数)？ dcf响应相量& H(jw) 激励相量戍 H(jw)= 2.网络函数用来描述什么？ jw CR+1 描述电路响应随频率变化的特性，即响应的频率特性 日(w) ◆HGo)川 HUw)=HUw)e)相频响应 0.707 幅频响应 909. @c (b) U& H(jw)= H(jw)= (a) UjCR+1 V1+(CR) 幅频响应 相频响应 g(w)=-arctan(wCR)

知识点回顾 1. 什么是网络函数（传输函数）？ def ( ) F Y H jw = & & 响应相量 激励相量 U S  UC  R j C 1 1 ( ) 1 C S U H j U j CR w w = = + & & 2. 网络函数用来描述什么？ 描述电路响应随频率变化的特性，即响应的频率特性 ( ) ( ) e ( ) j H j H j q w w = w 幅频响应 相频响应 1 ( ) 1 C S U H j U j CR w w = = + & & ( ) 2 1 ( ) 1 H j C R w w = + q w w ( ) arct an( ) = - C R 1 0.707 0 ω C ω (a) |H(jω)| 幅频响应 0 ω -45° -90° θ(ω) (b) ω C 相频响应

知识点回顾 3.如何根据幅频响应，定义通带、止带、截止角频率？ 通带：H(Go/Hmax>0.707的频率范围； 止带：HGjo/Hmax<0.707的频率范围； 截止角频率（半功率点频率)：二者的边界角频率o 4HGo川 0.707 H(jw)= jo C jw CR+1 0 Oc (a) 通带：w?[0,we)0,。 截止角频率w。= 低 止带：w?(w,￥)

知识点回顾 3. 如何根据幅频响应，定义通带、止带、截止角频率？ U S  UC  R j C 1 1 ( ) 1 C S U H j U j CR w w = = + & & 1 0.707 0 ω C ω (a) |H(jω)| 通带：|H(jω)|/Hmax > 0.707的频率范围； 止带：|H(jω)|/Hmax < 0.707的频率范围； 截止角频率（半功率点频率）：二者的边界角频率ωC 1 c R C 截止角频率w = 1 ( , ) ( , ) 1 [0, ) [0, ) c c R C C R w w w w ¥ ? 止带： ? ? 通带： 低 通

知识点回顾 4.如何判定低通、高通、全通？ R H(j) 0.707 低通函数 H(jo)=Ho Wc Uc j0+0。 0 OC (a) 高通函数 H(jo)=Ho 晓 1 j0+0c H(jw)= 咚jwCR+1 截止角频率"。= RC 全通函数 H(jo)=H。 J0-0c j0+0c 1 H(jw)= 1/(RC) juCR+1 jw+1/(RC)jw+we 其实直接判定也可以，分母上只要是按照ω的1阶和0阶组合即可！

知识点回顾 4. 如何判定低通、高通、全通？ U S  UC  R j C 1 1 ( ) 1 C S U H j U j CR w w = = + & & 1 0.707 0 ω C ω (a) |H(jω)| 1 c R C 截止角频率w = 1 / ( ) 1 / 1 ( ) = = 1 ( ) c c R C H R R C j j j C j w w w w w w = + + + C C j H j H     + = 0 低通函数 ( ) C j H j H     + =  j 高通函数 ( ) C C j H j H      + − = j ( ) 全通函数 0 其实直接判定也可以，分母上只要是按照ω的1阶和0阶组合即可！

5.2一阶电路和二阶电路的频率响应 一 阶电路 例1如图C电路，若以电容电压)。作输出，其网络函数为 1 1 H(jo)= Uc jo C RC @c 1 R+ 10+ j0+0c jo 低通函数 若以电阻电压U作输出，其网络函数为 UR R H(j0)= jo 同一电路，不同 R+ 10+ j0+0c 响应的滤波特性 jo C RC 不同！ 高通函数

C S R U UC  U R  UC  C C S C j RC j RC j C R j C U U H j        + = + = + = = 1 1 1 1 ( )   若以电阻电压 U  R 作输出，其网络函数为 S C R j j R C j j j C R R U U H j        + = + = + = = 1 1 ( )   例1 如图RC电路，若以电容电压 作输出，其网络函数为 5.2 一阶电路和二阶电路的频率响应 一、 一阶电路 低通函数 高通函数 同一电路，不同 响应的滤波特性 不同！

5.2一阶电路和二阶电路的频率响应 二、 二阶电路 二阶电路按频率响应可分为：低通、高通、带通、带阻和全通 低通函数 带通、 带阻是一阶无法实现的 带阻函数 H(jo)=Ho H(o)=H。 (j@)+o (a}+(jo)+a 高通函数 Q (o）+o6 9 H(Ujo）=H (jo)2 全通函数 (Uo+%(o）+ (jo)-%(jo)+of 带通函数 H(jo)=Ho (a}+Go)+o (j0) H(j@)=Ho Q ω和Q是什么？先保留疑问 2（j0)+o 听我细细分解！

二阶电路按频率响应可分为：低通、高通、带通、带阻和全通 ( ) 2 0 0 2 2 0 0 ( ) ( ) 低通函数       + + = j Q j H j H ( ) 2 0 0 2 2 ( ) （j ） ( ) 高通函数       + + =  j Q j H j H ( ) 2 0 0 2 0 0 ( ) （j ） ( ) 带通函数        + + = j Q j Q H j H ( ) 2 0 0 2 2 0 2 ( ) （j ） ( ) 带阻函数        + + + =  j Q j H j H ( ) 2 0 0 2 2 0 2 0 0 ( ) （j ） ( ) ( ) 全通函数          + + − + = j Q j j Q H j H 5.2 一阶电路和二阶电路的频率响应 二、 二阶电路 带通、带阻是一阶无法实现的 ω0和Q是什么？先保留疑问， 听我细细分解！

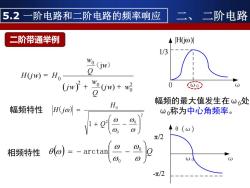
5.2一阶电路和二阶电路的频率响应 二、二阶电路 二阶带通举例 ◆H(Go 1/3 wo(jw) H(jw)=Ho wo 幅频的最大值发生在ω处 幅频特性 Ho H(jo)= ω，称为中心角频率。 1+Q 0_0g 00 π/2 相频特性o)=-arctan 000 G π/2

幅频特性 2 0 0 2 0 1 ( )       + − =      Q H H j ω0 ω θ(ω) π/2 -π/2 5.2 一阶电路和二阶电路的频率响应 二、 二阶电路 ( ) Q      = − −       0 0 相频特性 arctan 二阶带通举例 0 ω0 ω 1/3 |H(jω)| 幅频的最大值发生在ω0处， ω0称为中心角频率。 ( ) 0 0 2 0 2 0 j ( ) ( ) Q H j H j j Q w w w w w w w = + + （ ）

5.2一阶电路和二阶电路的频率响应 二、二阶电路 当H(jω)|下降到其最大值的0.707倍时，对 ◆HGo)川 应的频率称为截止频率，用ωc1、 wc2表示。 1/3 H(jo) 1 1 H max 1+02 0c_ 00 @c 00c1000c2 G @C _- 1 +1 0c2= 00 20 20 00 20 20 通频带 ωc1w〈ωc2的频率范围为通带。通带的宽度称为带宽或通频带， 用B表示。 B=0C2-0C1= 00 (rad/s) 或B (H2)

通频带 当|H(jω)|下降到其最大值的0.707倍时，对 应的频率称为截止频率，用ωC1、 ωC2表示。 2 1 1 ( ) 1 2 0 0 2 max =         + − = C C Q H H j      ωC1< ω < ωC2的频率范围为通带。通带的宽度称为带宽或通频带， 用B表示。 (rad/s) 0 2 1 Q B C C  =  − = ( ) 0 Hz Q f 或B = 5.2 一阶电路和二阶电路的频率响应 二、 二阶电路 0 ω0 ω 1/3 |H(jω)| C1 C2 B 1 2 1 2 1 1 2 1 2 1 2 0 2 2 0 1 +         + = +         = − + Q Q Q Q C C    

5.2一阶电路和二阶电路的频率响应 二、二阶电路 二阶带阻举例 joC 3 joC 例3如图双T电路是一个带阻电路。若以U, 1 为激励，以U,2为响应，求电压比函 1/R 数H(j0)=U2/心1，并分析其频率特性。①心， 2/R0卡jo2C 节点法 节点2：(joC+1/R)02-joCU3-(1/R)04=0 节点3：(joC+j0C+2/R)U,-joCU,-joCU2=0 节点4：(Ujo2C+1/R+1VR)U4-(1/R)U1-(1/R)U,=0

例3 如图双T电路是一个带阻电路。若以 为激励，以 为响应，求电压比函 数 ，并分析其频率特性。 节点法 U1 +− U2 +− C R C 2CR R 2 U1 2 1 H j U U ( )  = U2 节点2： 节点3： 节点4： 2 3 4 ( 1 ) (1 ) 0 j C R U j CU R U   + − − = 3 1 2 ( 2 ) 0 j C j C R U j CU j CU     + + − − = U1 +− U2 +− j C 1 R j C j C 2 1 2 3 4 1 R 2 R 4 1 2 ( 2 1 1 ) (1 ) (1 ) 0 j C R R U R U R U  + + − − = 5.2 一阶电路和二阶电路的频率响应 二、 二阶电路 二阶带阻举例

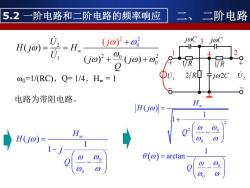
5.2一阶电路和二阶电路的频率响应 二、二阶电路 joC 3 H(j)= =Ho Uo)2+0 U o}'+%Uo)+o6尿 Q0=1/(RC),Q=1/4,H。=1 2/R j02C 电路为带阻电路。 H H(j@)= H(j@)= )arctan

2 2 2 1 2 2 0 0 0 ( ) ( ) ( ) ( ) U H j H U j j j Q         + = = + + 电路为带阻电路。 ω0=1/(RC)，Q= 1/4，H∞ = 1 5.2 一阶电路和二阶电路的频率响应 二、 二阶电路 U1 +− U2 +− j C 1 R j C j C 2 1 2 3 4 1 R 2 R 0 0 ( ) 1 1 H H j j Q       = −     −   ( ) 0 0 1 arctan Q       =     −   2 2 0 0 ( ) 1 1 H H j Q       = +     −  

5.2一阶电路和二阶电路的频率响应 二、二阶电路 幅频特性与相频特性曲线 A0(o) H(jo π 2 @o 0 2 在中心角频率w=ω处，H(jω)=0，日(w)=±T/2,ω也称为 陷波角频率。 在0=∞和0=0处，HG0)片HG∞)=H∞=1,0(0)=0（∞）=0。 该电路常用作高频陷波电路

幅频特性与相频特性曲线 在中心角频率ω＝ω0处，|H(jω0)|=0，θ(ω)=±π/2, ω0也称为 陷波角频率。 H j ( )  0 0  1  ( ) 0 0  2  2  − 在ω＝∞和ω＝0处，|H(j0)|= |H(j∞)|= H∞= 1，θ(0)= θ(∞)=0。 该电路常用作高频陷波电路。 5.2 一阶电路和二阶电路的频率响应 二、 二阶电路