西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.5 矩阵的分块

§4.5矩阵的分块 一、分块矩阵的概念 二、分块矩阵的运算 三、准对角矩阵
一、分块矩阵的概念 二、分块矩阵的运算 三、准对角矩阵

一、分块矩阵的概念定义设A是一个矩阵,在A的行或列之间加上一些线,把这个矩阵分成若干小块.用这种方法被分成若千小块的矩阵叫做一个分块矩阵每一个分块的方法叫做A一种分法84.5矩阵的分块
§4.5 矩阵的分块 一、分块矩阵的概念 定义 设A是一个矩阵,在A的行或列之间加上 一些线,把这个矩阵分成若干小块.用这种 方法被分成若干小块的矩阵叫做一个分块矩阵. 每一个分块的方法叫做A一种分法.

特殊分法设矩阵 A=(a,)sn"(A)A2按行分块 A=其中 A, =(ai1,ai2,"",ain),:i=1,2,..,s.A.ajanj按列分块A=(A,Az,,A),其中 A,-..j =1,2,...,n.an)84.5矩阵的分块A
§4.5 矩阵的分块 特殊分法 按行分块 1 2 , s A A A A = 其中 1 2 ( , , , ), A a a a i i i in = 按列分块 A A A A = ( 1 2 , , , n ) ,其中 1 2 , j j j nj a a A a = 设矩阵 ( ) , A a = ij s n j n = 1,2, , . i s = 1,2, ,
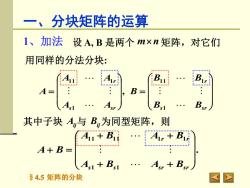
一、分块矩阵的运算1、加法设A,B是两个mxn矩阵,对它们用同样的分法分块:(B.)Bi.(AnAr......A=B=BsrBs1As1Asr其中子块A,与B,为同型矩阵,则Al1 + BlAl, + Br,A+B=Asr + BsrAs1 + Bs184.5矩阵的分块V
§4.5 矩阵的分块 = = s sr r s sr r B B B B B A A A A A 1 1 1 1 1 1 1 1 , 1、加法 设 A, B 是两个 m n 矩阵,对它们 一、分块矩阵的运算 . 1 1 1 1 1 1 1 1 + + + + + = s s sr sr r r A B A B A B A B A B 用同样的分法分块: 其中子块 Aij 与 Bij 为同型矩阵,则

2、数量乘法AaEP,则设分块矩阵A=...A.A,1(2Al12AirA=·.2As1Asr84.5矩阵的分块一1
§4.5 矩阵的分块 2、数量乘法 . 1 1 1 1 = s sr r A A A A A 设分块矩阵 11 1 1 , , r s sr A A A P A A = 则

把矩阵A=(ai)mxn,B=(b)n分块成3、乘法Bi1ABirAtA=B=:-Bt1BtrAs1As其中Ai1,Ai2,,A,的列数分别等于B,B2j,,Bi的行数,那末(Cu1Car:AB=(Cs1...CZAB, (i=l,.,s; j=1,.,r)其中Ci=k=l84.5矩阵的分块区区
§4.5 矩阵的分块 , , 1 1 1 1 1 1 1 1 = = t tr r s st t B B B B B A A A A A 的行数 那 末 其 中 的列数分别等于 , , , , , , , Ai1 Ai 2 Ai t B1 j B2 j Bi j = s sr r C C C C AB 1 11 1 ( 1, , ; 1, , ). 1 C A B i s j r k j t k i j = i k = = = 其 中 3、乘法 把矩阵 ( ) , ( ) A a B b = = ik m n kj n p 分块成
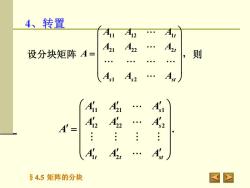
4、转置AuA12AA21A22A设分块矩阵 A=则As1AAstAlAzA's1A2A'A's24V:AAA'84.5矩阵的分块
§4.5 矩阵的分块 11 21 1 12 22 2 1 2 . s s t t st A A A A A A A A A A = 设分块矩阵 11 12 1 21 22 2 1 2 , t t s s st A A A A A A A A A A = 则 4、转置

设例1 110--2A=B0求 AB.4.5矩阵的分块
§4.5 矩阵的分块 例1 设 , 1 1 0 1 1 2 1 0 0 1 0 0 1 0 0 0 − A = , 1 1 2 0 1 0 4 1 1 2 0 1 1 0 1 0 − − − B = 求 AB

解把A,B分块成Bi1EBB21B22184.5矩阵的分块
§4.5 矩阵的分块 解 把A,B分块成 = 0 1 1 0 0 1 1 0 A 0 0 0 0 1 1 − 1 2 , = E E O A1 − − − = 1 1 2 0 1 0 4 1 1 2 0 1 1 0 1 0 B ( ) = B11 E B21 B22

E0EBu1则ABB22)EB21AlBu1EA +B,A,Bu + B21又 A,B + B21,)=-22/+1+B,4.5矩阵的分块
§4.5 矩阵的分块 则 = 21 22 11 1 B B B E A E E O AB . 1 11 21 1 22 11 + + = A B B A B B E 又 A1B11 + B21 − − + − − = 1 1 1 0 1 2 1 0 1 1 1 2 − − + − = 1 1 1 0 0 2 3 4 , 1 1 2 4 − − = + − + = 2 0 4 1 1 1 1 2 A1 B22 , 3 1 3 3 =
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.4 矩阵的逆.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.3 矩阵乘积的行列式.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.2 矩阵的运算.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.1 矩阵的概念.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.6 线性方程组解的结构.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.5 线性方程组有解判别定理.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.4 矩阵的秩.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.3 线性相关性.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.2 n维向量空间.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.1 消元法.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第二章 行列式 2.8 Laplace定理(拉普拉斯定理、行列式乘法法则).ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第二章 行列式 2.7 Cramer法则.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第二章 行列式 2.6 行列式按行(列)展开.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第二章 行列式 2.5 行列式的计算.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第二章 行列式 2.4 n级行列式的性质.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第二章 行列式 2.3 n级行列式.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第二章 行列式 2.2 排列.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第二章 行列式 2.1 引言.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第一章 多项式 1.9 有理系数多项式.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第一章 多项式 1.8 复、实系数多项式的因式分解.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.6 初等矩阵.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.7 分块乘法的初等变换及应用举例.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第十章 双线性函数 10.1 线性函数.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第十章 双线性函数 10.2 对偶空间.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第十章 双线性函数 10.3 双线性函数.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第十章 双线性函数 10.4 对称双线性函数.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第五章 二次型 5.1 二次型的矩阵表示.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第五章 二次型 5.2 标准形.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第五章 二次型 5.3 唯一性.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第五章 二次型 5.4 正定二次型.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.1 集合·映射.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.2 线性空间的定义与简单性质.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.3 维数·基与坐标.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.4 基变换与坐标变换.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.5 线性子空间.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.6 子空间的交与和.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.7 子空间的直和.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.8 线性空间的同构.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第七章 线性变换 7.1 线性变换的定义.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第七章 线性变换 7.2 线性变换的运算.ppt
