深圳大学：《系统动力学》课程教学资源（PPT课件）第六讲 现代控制理论 Modern Control Theory Chapter 1 控制系统的状态空间表达式 State space description of control systems

现代控制理论 Modern Control Theory

现代控制理论 Modern Control Theory

控制系统的状态空间表达式 Chapter 1 State space description of control systems

控制系统的状态空间表达式 Chapter 1 State space description of control systems

本章内容 ●状态变量及状态空间表达式 ●状态空间表达式的模拟结构图 ·状态空间表达式的建立(1) ●状态空间表达式的建立(2) 。状态矢量的线性变换 ·由传递函数求状态方程 ●由状态空间表达式求传递函数阵 ● 离散系统的状态空间表达式 ●时变系统和非线性系统的状态空间表达式

本章内容 ⚫ 状态变量及状态空间表达式 ⚫ 状态空间表达式的模拟结构图 ⚫ 状态空间表达式的建立(1) ⚫ 状态空间表达式的建立(2) ⚫ 状态矢量的线性变换 ⚫ 由传递函数求状态方程 ⚫ 由状态空间表达式求传递函数阵 ⚫ 离散系统的状态空间表达式 ⚫ 时变系统和非线性系统的状态空间表达式

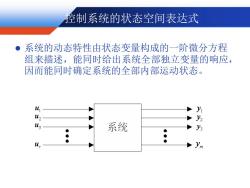
控制系统的状态空间表达式 ●系统的动态特性由状态变量构成的一阶微分方程 组来描述，能同时给出系统全部独立变量的响应， 因而能同时确定系统的全部内部运动状态。 42 2 系统 y3 ● u ym

控制系统的状态空间表达式 ⚫ 系统的动态特性由状态变量构成的一阶微分方程 组来描述，能同时给出系统全部独立变量的响应， 因而能同时确定系统的全部内部运动状态

状态变量及状态空间表达式 State space description of control systems

状态变量及状态空间表达式 State space description of control systems

状态变量及状态空间表达式 ●状态变量(State variables) -状态：表征系统运动的信息和行为 -状态变量：能完全表示系统运动状态的最小个数的一 组变量 X1(t),X2(t),.,Xn(t) ●状态向量(State vectors) 由状态变量构成的向量X(t) x(t)=x(t),x2(1),x(1)..x(t)

状态变量及状态空间表达式 ⚫ 状态变量 (State variables) – 状态：表征系统运动的信息和行为 – 状态变量：能完全表示系统运动状态的最小个数的一 组变量 x1(t), x2(t), …, xn(t) ⚫ 状态向量(State vectors) 由状态变量构成的向量 x(t)

状态变量及状态空间表达式 状态空间(State space) - 以各状态变量x1(t)X2(t)…Xn(t)为坐标轴组的 几维空间。 状态轨迹：在特定时刻t,状态向量可用状态空间的 一个点来表示，随着时间的推移，x()将在状态空 间描绘出一条轨迹线。 ●状态方程(State equations) 由系统的状态变量与输入变量之间的关系构成的一阶 微分方程组

状态变量及状态空间表达式 ⚫ 状态空间 (State space) – 以各状态变量x1(t),x2(t),…… xn(t)为坐标轴组的 几维空间。 – 状态轨迹：在特定时刻t，状态向量可用状态空间的 一个点来表示，随着时间的推移，x(t)将在状态空 间描绘出一条轨迹线。 ⚫ 状态方程 (State equations) – 由系统的状态变量与输入变量之间的关系构成的一阶 微分方程组

状态变量及状态空间表达式 例设有一质量弹簧阻尼系统。试确定其状态变量和状态方 程。 解：系统动态方程 y(f F(t)-ky(t)-f.j(t)=m- y F(t) NN dt mj(t)+f.i(t)+ky(t)=F(t) 设y(t)=x,(t)(t)=x2(t) (t)=(t) 0=0-A0+02 m

状态变量及状态空间表达式 例设有一质量弹簧阻尼系统。试确定其状态变量和状态方 程。     + + = − − = ( ) . ( ) ( ) ( ) ( ) ( ) . ( ) 2 my t f y t k y t F t dt d y F t k y t f y t m    ( ) ( ) 1 设y t = x t ( ) ( ) 2 y  t = x t     = − − + = ( )........(2) 1 ( ) ( ) ( ) ( ) ( )............................................(1) 2 1 F t m y t m k y t m f x t x t y t     解：系统动态方程

状态变量及状态空间表达式 例设有一质量弹簧阻尼系统。试确定其状态变量和状态方 程。 x1(t)=x2(t) 0=x0-x0+F0 状态方程的标准形式： (t)=Ax(t)+Bu(t) (A:系统矩阵B:输入矩阵)

状态变量及状态空间表达式 例 设有一质量弹簧阻尼系统。试确定其状态变量和状态方 程。 ( ) 1 0 ( ) 0 1 ( ) ( ) ( ) 2 1 2 1 F t m x t x t m f m k x t x t         +               − −      ＝       = − − + = ( ) 1 ( ) ( ) ( ) ( ) ( ) 2 1 2 1 2 F t m x t m f x t m k x t x t x t   状态方程的标准形式： x (t) = Ax(t) + Bu(t) （A：系统矩阵 B：输入矩阵）

状态变量及状态空间表达式 输出方程(Output equation) 系统的输出量与状态变量之间的关系 0ml[网 y(t)=Cx(t) (C:输出矩阵)

状态变量及状态空间表达式 ⚫ 输出方程 (Output equation) 系统的输出量与状态变量之间的关系         = = ( ) ( ) ( ) ( ) 1 0 2 1 1 x t x t y t x t y(t) = Cx(t) (C:输出矩阵）