南京大学：《计算机问题求解》课程教学资源（课件讲稿）图论的其它专题（平面图与图着色）

计算机问题求解一论题3-14 图论中的其它专题 2016年12月06日

计算机问题求解 – 论题3-14 - 图论中的其它专题 2016年12月06日

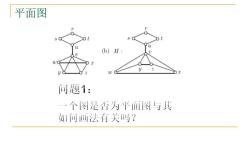
平面图 (b)H: 2 问题1： 一个图是否为平面图与其 如何画法有关吗？

平面图

Theorem 9.1 (The Euler Identity)If G is a connected plane graph of order n,size m and having r regions,then n-m+r=2. 证明要点： 1,树是满足欧拉公式 2,反证法：如果除树外，欧拉公式不成立 如果我们用归纳 2.1找一个边最小的图 法证明该定理， 2.1.1必定存在回路 该如何归纳？ 2.2去除回路上一条边，构造新图 2.2.1新图有n个点，m-1条边，r-1个区域 2.3新图满足欧拉公式（原图是最小的） 2.3.1n-(m-1)+(r-1)=2 2.3.2n-m+r=2 2.4矛盾 3,欧拉公式满足

证明要点： 1，树是满足欧拉公式 2，反证法：如果除树外，欧拉公式不成立 2.1 找一个边最小的图 2.1.1 必定存在回路 2.2 去除回路上一条边，构造新图 2.2.1 新图有n个点，m-1条边，r-1个区域 2.3 新图满足欧拉公式（原图是最小的） 2.3.1 n-(m-1)+(r-1) = 2 2.3.2 n-m+r=2 2.4 矛盾 3，欧拉公式满足 如果我们用归纳 法证明该定理， 该如何归纳？

问题2： 你是否在哪里里还见过“这个” 欧拉公式？

问题3： 必要条件可以判断什么？ 欧拉公式在实际判断平面 图时有用吗？

简单连通平面图的必要条件 ■欧拉公式的推论：若G是简单连通平面图（≥3），则 m≤3n-6。 口证明：至少3个顶点的简单图G中，面的最小度数是3， .3r≤2m,根据欧拉公式：3r=3m+6-3n,.3m+6-3n≤2m,即： m≤3n-6。 ■K不是平面图：在K,中，n=5,m=10,3n-6=9

简单连通平面图的必要条件  欧拉公式的推论：若G是简单连通平面图(n3), 则 m3n-6。  证明：至少3个顶点的简单图G中，面的最小度数是3， 3r2m, 根据欧拉公式：3r=3m+6-3n, 3m+6-3n2m, 即： m3n-6。  K5不是平面图：在K5中，n=5, m=10, 3n-6=9

问题4： 上述推论不能证明K3.3是 非平面图，你能推出一个 类似的推论用于K33吗？

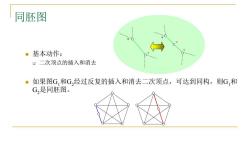
同胚图 ■基本动作： 口二次顶点的插入和消去 。1 如果图G,和G,经过反复的插入和消去二次顶点，可达到同构，则G,和 G是同胚图

同胚图  基本动作：  二次顶点的插入和消去  如果图G1和G2经过反复的插入和消去二次顶点，可达到同构，则G1和 G2是同胚图。 u u v v w

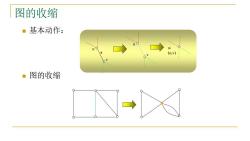
图的收缩 ■基本动作： u d u (u,v) ■图的收缩

图的收缩  基本动作：  图的收缩 u v u v e w (u,v)

平面图的充分必要条件 Kuratowsky定理 口图G是平面图当且仅当G中不含与K,或者K?3同胚的子图，也不含可以 收缩到K或者K3.3的子图

平面图的充分必要条件  Kuratowsky定理  图G是平面图当且仅当G中不含与K5或者K3,3同胚的子图,也不含可以 收缩到K5或者K3,3的子图