南京大学：《计算机问题求解》课程教学资源（PPT课件讲稿）串匹配

计算机问题求解一论题4-11 串匹配 2017年5月3日

计算机问题求解 – 论题4-11 - 串匹配 2017年5月3日

问题1： 什么是string-matching problem,直观上？形式上？

string-matching problem

text T a b c a a a b a b a S=3 pattern a a we say that pattern P occurs with shift s in text T (or,equivalently,that pattern P occurs beginning at position s+1 in text T)if 0≤s≤n-m and T5+l.s+m=P[l.m(that is,.ifT5+j】=P[Ujl,for 1jm).If P occurs with shift s in T,then we call s a valid shift;otherwise, we call s an invalid shift.The string-matching problem is the problem of finding all valid shifts with which a given pattern P occurs in a given text T

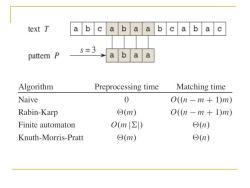
text T a b a b a a b a b a c S=3 pattern P a b a a Algorithm Preprocessing time Matching time Naive 0 O(n-m+1)m) Rabin-Karp ⊙(m) O(n-m+1)m) Finite automaton O(mΣ) ⊙(n) Knuth-Morris-Pratt ⊙(m) ©(n)

最容易想到的算法 a a a b a a a b c a a a b a a a b S=0 =3 a b a b 问题2： 为什么称它为nave”算法？

最容易想到的算法

NAIVE-STRING-MATCHER(T,P) 1 n T.length 2 m =P.length 3 for s 0 to n-m 4 ifP1..m]==T[s+1..s+m 5 print"Pattern occurs with shift"s 问题3： 为什么在最坏情况下复杂 度是平方级的？

问题4： 你能否说说nave算法 有什么问题，为什么有 可能改进？

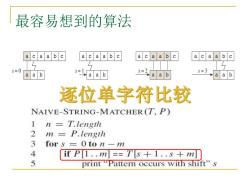
最容易想到的算法 a a b a a a b a a b a a a b S=0 5=3 a a b a a a a b 逐位单字符比较 NAIVE-STRING-MATCHER(T,P) 1 n T.length 2 m= P.length 3 for s =0to n-m 4 ifP[1..m==T[s+1..s+m 5 print "Pattern occurs with shift"s

最容易想到的算法

问题5， Rabin-Karp算法的基本 思想是什么？ For expository purposes,let us assume that=,1,2..,so that each character is a decimal digit.(In the general case,we can assume that each charac- ter is a digit in radix-d notation,where d)We can then view a string of k consecutive characters as representing a length-k decimal number.The character string 31415 thus corresponds to the decimal number 31,415

Preprocessing 问题6： Rabin-Karp算法是采用“预处理 方式的算法？何为“预处理”，这 个算法预处理的结果是什么？ 31415→m0d13→ 7 1234567891011121314151617 1819 2359023141526739921 mod 13 8931101784510117911

Preprocessing