上海交通大学：《弹塑性力学》课程教学资源（讲义）弹性与塑性力学解题方法（3/3）

§4一5逆解法和半逆解法 、 简支梁受均布载荷一半逆解法 材料力学已知解 弹性体的边界受力情况 设定某一 应力分量 →p 量纲分析法 2 74p=0 是否正 确解谷 边界条件 ←其它应力分量 应变分量 → 位移分量 周上我人 ME6011弹性塑性力学 49 例：单位厚度的矩形截面梁，受到均布力作用，试求应力分量。 (不计体力) 解：（一）确定应力函数： q o,=f(y) 82o 0y= dx2 9/ 是=f)） h 0 X 之f)+1)+2) 74p=0 +20p 89 =0 Ox4 受力分析： B20p 面力在y方向有变化， 09-0 上边界 h=g ar= 8' =- y=- 2 下边界 h=0 a'g-'f2+xd'f巴+'f 2办4 少 圆上海遵 ME6011弹性塑性力学 50 1

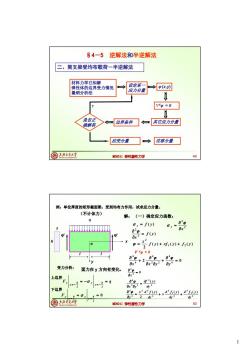
1 ME6011 弹性塑性力学 §4－5 逆解法和半逆解法 二、简支梁受均布载荷－半逆解法 材料力学已知解 弹性体的边界受力情况 量纲分析法 x,y) 4 = 0 应变分量 设定某一 应力分量 是否正 边界条件 其它应力分量 确解答 位移分量 ？ 49 ME6011 弹性塑性力学  4 = 0 受力分析： 面力在 y 方向有变化， F q h y h y y y        2 2  例：单位厚度的矩形截面梁，受到均布力作用，试求应力分量。 解： （一）确定应力函数： （不计体力） h 1 l x y o ql q l ql 0 2 2     h y h y y F y  f ( y )  y  2 2 x y      ( ) 2 2 f y x     ( ) ( ) ( ) 2 1 2 2 f y xf y f y x     2 0 4 4 2 2 4 4 4           x x y y    0 4 4    x  2 2 2 2 4 ( ) dy df y x y      4 2 4 4 1 4 4 2 4 4 4 ( ) ( ) ( ) 2 dy d f y dy d f y x dy x d f y y       50 上边界 下边界

1dfDx2+4fx+f2+2f=0 2y4 你 少2 1d4fy)=0 24 f(y)=Ay3+By2+Cy+D d'f()=0 f1(y)=E3+2+G园 h()2) 2)=-Ay5-By+3+2 2 10 6 =-12Ay-4B My N p=号(++g+D)+6+2+@) 2 -+3+3 圈上活庆大峰 ME6011弹性塑性力学 51 (二)应力分量： 8'o Ox= =3++0+小+6+5+0 02 0y= 09 -++ a2 8o T=- axoy 264+2B)+x6面+2F)-23-22+6+2L 0,=A3+2+C+D rg=-x电A4y2+2B+C）-3E2+2+G) 圆上1大峰 ME6011弹性塑性力学 52 2

2 ME6011 弹性塑性力学 0 ( ) 2 ( ) ( ) ( ) 2 1 2 2 4 2 4 4 1 4 2 4 4     dy d f y dy d f y x dy d f y x dy d f y 0 ( ) 2 1 4 4  dy d f y f y  Ay  By  Cy  D 3 2 ( ) 0 ( ) 4 1 4  dy d f y f y  Ey  Fy  Gy  H 3 2 1 ( ) 2 2 4 2 4 ( ) 2 ( ) dy d f y dy d f y    12 Ay  4B My N y Ky Ly B y A f y        5 4 3 2 2 10 6 ( )     5 4 3 2 3 2 3 2 2 10 6 2 y Ky Ly B y A Ay By Cy D x Ey Fy Gy x             51 ME6011 弹性塑性力学                     x y x y xy y x       2 2 2 2 2 （二）应力分量：     5 4 3 2 3 2 3 2 2 10 6 2 y Ky Ly B y A Ay By Cy D x Ey Fy Gy x                Ay B x Ey F Ay By Ky L x x 6 2 6 2 2 2 6 2 2 3 2 2          y  Ay  By  Cy  D 3 2  x  Ay By C   Ey Fy G  xy   3  2   3  2  2 2  52

(三)确定待定系数： 0x=号6+2B)H6+2F)-23-2B2+6+2 0,=A3+B2+G+D (tg=-x62+2+C 3Ey2+2Fy+G) q 对称性： ox(-x,y)=ox(x,y) gl 6E+2F=0 E=F=0 o,(-x,y)=o,(x,y) ix(-x,y)=-tg(x,y) 3Ey2+2y+G=0 G=0 ©上活秋峰 M6011弹性塑性力学 53 边界条件：A、B、C、D、K、L 岁(6A+2B)-2A3-2B2+6+ o,=Ay3+By2+Cy+D 1 L =-x(3Ay2+2By+c) h y=21=0,m=1 2 Tg=2=0 4h2+Bh+C=0 3 2q A=- 0,-12=0 4h3+h2+ 1 1 B=0 Ch+D=0 3q h 4 C= y=- 2h x=0 3Ah2-Bh+C=0 D=- 14h3+B2- 2 0y=-4 1 Ch+D=-q 圆上1大峰 ME601弹性塑性力学 54 3

3 ME6011 弹性塑性力学 （三）确定待定系数：    Ay B x Ey F Ay By Ky L x x 6 2 6 2 2 2 6 2 2 3 2 2          y  Ay  By  Cy  D 3 2  x  Ay By C   Ey Fy G  xy   3  2   3  2  2 2  h 1 l x y o ql q l ql ( x , y ) ( x , y )  x    x ( x , y ) ( x , y )  y    y ( x , y ) ( x , y ) xy xy     对称性： 6Ey  2F  0 E  F  0 3 2 0 2 Ey  Fy  G  G  0 53 ME6011 弹性塑性力学   Ay B Ay By Ky L x x 6 2 2 2 6 2 2 3 2 2        y  Ay  By  Cy  D 3 2  x  Ay By C  xy   3  2  2  h 1 l x y o ql q l ql 边界条件：A、B、C、D、K、L : 2 h y  l  0, m  1 0  xy y  h / 2  0 4 3 2 Ah  Bh  C   y y  h / 2  0 0 2 1 4 1 8 1 3 2 Ah  Bh  Ch  D  : 2 h y   0 4 3 2  xy  0 Ah  Bh  C   y   q  Ah  Bh  Ch  D   q 2 1 4 1 8 1 3 2 2 2 3 0 2 3 q D h q C B h q A       54

应力分量：K、L xs 692y+4w3 h3 9l2 9 h3 h3-0h 2qy 3 h3 34w4 +2h-2 9/ 6gxy2 3qx h 0 3-2h x=1: Oxx-1=Fx Exx-1=Fy h3 12 「olk=1=0 L=0 S 8 xx=dy =-gl 2=- M=g(2-x2 ∫oxx=1J=0 K= 9l2 h310h 圈上我大峰 ME6011弹性塑性力学 55 应力分量： My gx= X 弹性力学修正项 ，=-+-) 材料力学为零 9 与材力结果一致 9 梁的中间截面(x=0) 9 9/ 6 h=2:&-27% X h=l:&-6.7% 2h=l&-1.7% 圆上1大峰 ME6011弹性塑性力学 56 4

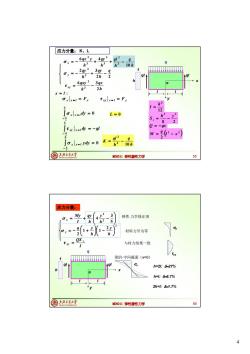
4 ME6011 弹性塑性力学 h 1 l x y o ql q l ql 应力分量： K、L x  l :  x x  l  Fx 0 2 2     dy h h  x x l xy x  l  F y  dy ql h h  xy x l     2 2  0 2 2     ydy h h  x x l Ky L h qy h qx y x 6 2 6 4 3 3 3 2       2 2 2 3 3 3 q h qy h qy  y     h qx h qxy xy 2 6 3 3 2    L  0 h q h ql K 10 3 2   h q h ql 10 3 2  12 3 h I  8 2 2 2 h y S z   Q   qx   2 2 2 l x q M   55 ME6011 弹性塑性力学            5 3 4 2 2 h y h qy I My  x h 1 l x y o ql q l ql 应力分量： 2 2 1 1 2                 h y h q y  y I QS z  xy  h=2l: 27% h=l: 6.7% 2h=l: 1.7% x y xy 56 弹性 力学修正项 材料力学为零 与材力结果一致 梁的·中间截面（x=0）

4一6边界上的φ及其导数的力学意义 一、用应力函数表示边界条件 los+msy=Fs 10 8'om0o=Fs o -m 2 cosa- axay 2 -sina 09=Fx axay Itx+moy Fy -10p+m r? -cosa 0Q=Fy axay o+sina axay &x2 cosa=- ,sina=- r d ds y B F Fx= 82o dy 8'o dx dy2 ds dxdy ds ..dy La F: ds dx x=7 8 ao dy a ap dx ayay ds ax ay ds ao F,=- dao X ds dy ds dx 圈上海式大峰 MB6011弹性塑性力学 57 二、边界上的仰及其导数 {) 考感AB边界上面力的合力和合力矩： F,=-) d(80 )。-+) -1-(熙)-() B X 人a d 〔)。-R+) ds dx MB=0g-Fk+-xaE,杰 国上清大峰 ME6011弹性塑性力学 58 5

5 ME6011 弹性塑性力学 A B 4－6 边界上的 及其导数的力学意义 一、用应力函数表示边界条件 x m xy Fx l    xy m y Fy l    Fx x y m y l         2 2 2 Fy x m x y l         2 2 2   Fx Fy n dx dy ds  Fx y x y            2 2 2 cos sin Fy x y x         2 2 2 cos sin     ds dx ds dy cos  ,sin   ds dx ds x y dy y Fx         2 2 2 ds dx ds x y dy y y Fx                                        ds y d Fx            ds x d Fy  x y x y 57 ME6011 弹性塑性力学            ds y d Fx            ds x d Fy  Fx Fy n A B dx dy ds  x y x y 二、边界上的 及其导数 考虑AB边界上面力的合力和合力矩： B A B A x x y y R F ds                           A B B A y y x x R F ds                       A x B y R y                        A y B x R x                           B A B y B A MB ( yB y)Fxds (x x )F ds 58

Mg=J(Yg-y)F,ds+j(x-xa)F,ds Fx= {) 8 w.-jn)j) d(ao ds dx 8p d dg bp +y -do A B MB=yB dp +xB bo +p日 A 4 0心 ay MB=yB ap bp bp +ax ap B B Ox) bp ap bp 0 +xA -yB A ay +ya +PB-PA 上毒成豆大警 ME6011弹性塑性力学 59 MB=-(YB-y4) -(n-x) dp +P8-PA =M+-(8)+0-8g+p, 〔) p ax y F n =R+ ds 《华 dx 三、边界上的心及其导数的力学意义 设： =b 9i-x 圆上1大峰 ME6011弹性塑性力学 60 6

6 ME6011 弹性塑性力学            ds y d Fx            ds x d Fy        B A B y B A B B x M ( y y)F ds (x x )F ds                         B A B B A B B x x x d y M y y d   ( ) ( )                                               B A B A B B A B B x xd y yd x x y M y                                              B A B A B B A B B d y y x d x x x y M y      B A B A B A B B A B B y y x x x x y M y                                         B A A B A A A B B A B B B A B B B y y y y x x x x x x x x y y y M y                                                                                             B B 59 ME6011 弹性塑性力学 B A A B A A B B A x x x y M y y                            (  ) ( ) A A B A A B B B A y y y x M x x                            (  ) ( ) A x B y R y                        a x A          Fx Fy n A B dx dy ds  x y x 三、边界上的 及其导数的力学意义 y 设： b y A            c y y x x A A A A A                         A y B x R x                     60

三、边界上的φ及其导数的力学意义 ap x)B =-R,+a y B ap a =Rx+b d )B ds dx PB=MB+axg +byg+c y >应力函数中一次项不影响应力分量 X 设：a= =0p4=0 ax =0b= y >称A为基点 bp =-R >AB段面力合力在y方向的分量。 ax)B bp ~AB段面力合力在x方向的分量。 B =Rx + R=MR 》AB段面力对B点取矩的代数和。 上活大峰 ME6011弹性塑性力学 61 例1：单位厚度的矩形截面梁，受均布力作用，试求边界上的应力函数及导数，并求 域内的应力分量。 PB=MB yB A ap 8p =Rx 9 ax =-Ry B B 6 bp op X Ox D AB 0 0 0 解：选A为基点： -()- BC 0 -q(b-y) 是0-3 CD 0 -qb 4b2 设： p=是b-2 DA q(b-y) 4b-y)2 国上清大峰 ME6011弹性塑性力学 62 7

7 ME6011 弹性塑性力学 M ax by c  B  B  B  B  R b y x B             Fx Fy n A B dx dy ds  x y x y 三、边界上的 及其导数的力学意义 R a x y B            0 A a x           设： 0 A b y            0  A  应力函数中一次项不影响应力分量  称A为基点 y B R x            AB段面力合力在 y 方向的分量。 x B R y             AB段面力合力在 x 方向的分量。  B  MB  AB段面力对B点取矩的代数和。 ＋ 61 ME6011 弹性塑性力学 例1：单位厚度的矩形截面梁，受均布力作用，试求边界上的应力函数及导数，并求 域内的应力分量。 x y C l q y B A D q b 解：选A为基点：  0                     A A A x y    y B R x           x B R y             B  MB AB BC CD DA x  y   000 0 0 0  q(b  y)  qb  q(b  y) 2 ( ) 2 b y q  2 ( ) 2 b y q  2 2 b q 2 ( ) 2 b y q 设：    62

p=是-川 0x=4 g,=0 7*p=0 T=0 D ap ap 另解：选D为基点： ax -()-(, DA 0 F AB 0 qb = 2 BC 0 ÷基点不同，应力函数不同，但 4v2 应力分量相同。 CD 0 0 0 周上我人 ME6011弹性塑性力学 63 4-7塑性力学的解题方法 塑性力学中的物理关系是非线性的，在具体求解 边值问题时往往遇到许多数学上的困难。 为此，塑性力学发展了许多行之有效的方法。 圆认座 ME6011弹性塑性力学 64 8

8 ME6011 弹性塑性力学 2 ( ) 2 b y q    0 4    q  x   0  y  0 xy  x y C l q y B A D q b 另解：选D为基点：  0                     D D D x y    AB BC CD DA x  y   0 0 0 0 0 0 qb qy 2 2 y q 2 2 b q qy 2 2 y q 2 2 y q    基点不同，应力函数不同，但 应力分量相同。 63 ME6011 弹性塑性力学 4-7 塑性力学的解题方法 塑性力学中的物理关系是非线性的，在具体求解 边值问题时往往遇到许多数学上的困难。 为此，塑性力学发展了许多行之有效的方法。 64

静定问题简单问题 特点：平衡方程、屈服条件的数目与所求未知量的 数目相等。 不用使用塑性力学中的非线性本构方程 塑性力学中的一维问题大多属于这类问题：旋转圆 盘、厚壁圆筒、厚壁圆球、实心和空心受扭圆轴、 各种截面梁的弹塑性弯曲等都属于这类问题。 」在求解这类问题时，一般都采用理想弹塑性力学模 型计算。 这类问题虽然求解简便，但在工程实际中却经常遇 到，因此很有应用价值。 周上活大 ME6011弹性塑性力学 65 界限法 界限法又称上、下限法 由于要找到能满足全部塑性力学方程的解是非常困 难的，因而若能找到满足一部分方程的解，又能对 这些解的性质作出估计，这样的解是很有意义的。 」下限法（静力法）：第一类方程包括平衡方程、屈 服条件和力的边界条件，这些条件称为静力条件， 在这些条件中不包括几何方面的要求。若某一个解 能满足上述的静力条件，则称为静力解。 用静力法求得的极限载荷一定小于或等于完全解所 求得的极限载荷。 ©上清大座 ME6011弹性塑性力学 66

9 ME6011 弹性塑性力学  静定问题 特点：平衡方程、屈服条件的数目与所求未知量的 数目相等。 不用使用塑性力学中的非线性本构方程  塑性力学中的一维问题大多属于这类问题：旋转圆 盘、厚壁圆筒、厚壁圆球、实心和空心受扭圆轴、 各种截面梁的弹塑性弯曲等都属于这类问题。  在求解这类问题时，一般都采用理想弹塑性力学模 型计算。  这类问题虽然求解简便，但在工程实际中却经常遇 到，因此很有应用价值。 简单问题 65 ME6011 弹性塑性力学  界限法 界限法又称上、下限法 由于要找到能满足全部塑性力学方程的解是非常困 难的，因而若能找到满足一部分方程的解，又能对 这些解的性质作出估计，这样的解是很有意义的。  下限法（静力法）：第一类方程包括平衡方程、屈 服条件和力的边界条件，这些条件称为静力条件， 在这些条件中不包括几何方面的要求。若某一个解 能满足上述的静力条件，则称为静力解。 用静力法求得的极限载荷一定小于或等于完全解所 求得的极限载荷。 66

上限法（机动法）：另一类方程包括外力作功等于 内部耗散功的条件以及结构的几何边界条件，这里 没有考虑静力方面的要求。 用机动法求得的极限载荷一般大于或等于完全解所 求得的极限载荷。 上限法在金属塑性成形问题中和板壳塑性极限分析 中获得了非常广泛的应用。 在上限法中，总可以按照某一破环机构根据虚功原理找出极 限载荷的上限值，而破坏机构又可以通过实验找到，最合理 的破坏模式也就是和实验结果一致的模式。 M6011弹性塑性力学 67 ·滑移线法 在塑性平面应变问题中，使用滑移线解题是一个有 效的方法。 金属材料产生塑性变形的基本机制是滑移，滑移的 结果形成滑移带，滑移带和最大剪应力的迹线方向 是重合的，因此最大剪应力的迹线称为滑移线。 」滑移线法就是利用塑性变形过程中的特点将问题转 化为建立滑移线场，然后再由滑移线的几何性质确 定各应力分量。 优点：将复杂的塑性力学问题转化为几何问题来分 析，避免了直接采用非线性本构方程的困难。 ©上海礼大空 ME6011弹性塑性力学 68 10

10 ME6011 弹性塑性力学  上限法（机动法）：另一类方程包括外力作功等于 内部耗散功的条件以及结构的几何边界条件，这里 没有考虑静力方面的要求。 用机动法求得的极限载荷一般大于或等于完全解所 求得的极限载荷。 上限法在金属塑性成形问题中和板壳塑性极限分析 中获得了非常广泛的应用。 在上限法中，总可以按照某一破环机构根据虚功原理找出极 限载荷的上限值，而破坏机构又可以通过实验找到，最合理 的破坏模式也就是和实验结果一致的模式。 67 ME6011 弹性塑性力学  滑移线法 在塑性平面应变问题中，使用滑移线解题是一个有 效的方法。  金属材料产生塑性变形的基本机制是滑移，滑移的 结果形成滑移带，滑移带和最大剪应力的迹线方向 是重合的，因此最大剪应力的迹线称为滑移线。  滑移线法就是利用塑性变形过程中的特点将问题转 化为建立滑移线场，然后再由滑移线的几何性质确 定各应力分量。  优点：将复杂的塑性力学问题转化为几何问题来分 析，避免了直接采用非线性本构方程的困难。 68