中国科学技术大学：《计算方法》课程教学课件（PPT讲稿）第7章 矩阵的特征值和特征向量

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第7章矩阵的特征值和特征向量 很多工程计算中，会遇到特征值和特征向量的计算，如： 机械、结构或电磁振动中的固有值问题；物理学中的各种临界 值等。这些特征值的计算往往意义重大

数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第7章 矩阵的特征值和特征向量 很多工程计算中，会遇到特征值和特征向量的计算，如： 机械、结构或电磁振动中的固有值问题；物理学中的各种临界 值等。这些特征值的计算往往意义重大

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 特征值：P,(2)=det(2I-A)=0的根2为矩阵A的特征值 特征向量：满足y=Ay的向量v为矩阵A的对于特征值人，的 特征向量 P,(2)称为矩阵A的特征多项式 P(入)是高次的多项式，它的求根是很困难的。没有数值方 法是通过求它的根来求矩阵的特征值。通常对某个特征值，可 以用些针对性的方法来求其近似值。若要求所有的特征值，则 可以对A做一系列的相似变换，“收敛”到对角阵或上（下)三 角阵，从而求得所有特征值的近似

数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 特征值： PA () = det(I − A) = 0 的根 为矩阵A的特征值 特征向量：满足 v Av i = 的向量v为矩阵A的对于特征值 的  i () PA 称为矩阵A的特征多项式 是高次的多项式，它的求根是很困难的。没有数值方 法是通过求它的根来求矩阵的特征值。通常对某个特征值，可 以用些针对性的方法来求其近似值。若要求所有的特征值，则 可以对A做一系列的相似变换，“收敛”到对角阵或上（下）三 角阵，从而求得所有特征值的近似。 () PA 特征向量

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 7.1幂法 矩阵的按模最大特征值往往表现为阈值。如：矩阵的谱半 径。幂法就是一种求矩阵按模最大特征值的方法，它是最经典 的方法。 幂法要求A有完备的特征向量系，即A有n个线性无关的 特征向量。在实践中，常遇到的实对称矩阵和特征值互不相 同的矩阵就具有这种性质。设A的特征值和特征向量如下： 特征值： 2≥22≥.≥2 特征向量：V1 V2 幂法可以求入Y,基本思想很简单

数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 7.1 幂法 矩阵的按模最大特征值往往表现为阈值。如：矩阵的谱半 径。幂法就是一种求矩阵按模最大特征值的方法，它是最经典 的方法。 幂法要求A有完备的特征向量系，即A有n个线性无关的 特征向量。在实践中，常遇到的实对称矩阵和特征值互不相 同的矩阵就具有这种性质。设A的特征值和特征向量如下： n n v v v 1 2 1 2  特征值：      特征向量： 幂法可以求 1 1  v ，基本思想很简单

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 设心，线性无关，取初值xo),作迭代 x(k+1)=Ax(k)=4k+lx(0) 设：x0=a4y+a22++,Vn 则有：x)=A(ay+ay2++n） =a4Ay+a2Ay2+.+aAv =ay,+232+.+Cn,yn

数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 设   n i i=1 v 线性无关，取初值 (0) x ，作迭代 ( 1) ( ) 1 (0) x Ax A x k+ k k+ = = 设： n n x = v + v ++ v 1 1 2 2 (0) n k n n k k n k n k k n n k k v v v A v A v A v x A v v v             = + + + = + + + = + + +    1 1 1 2 2 2 1 1 2 2 1 1 2 2 ( ) ( ) 则有：

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS (1)若：2>22≥.≥2 -a+喉 必1≠0则k足够大时，有 x=*(ay） xk+=2+(ay) 可见x,xk+)几乎仅差一个常数2 所以：≈xk+)/x) 任意分量相除 当≈x(+) 特征向量乘以任意数， 仍是特征向量

数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS （1）若： 1  2  n                 + +         = + n n k n k k k x v v  v        1 2 2 1 2 1 1 1 ( )  1  0 则k足够大时，有 ( ) 1 1 1 ( ) x v k k =   ( ) 1 1 1 1 ( 1) x v k k   + + = 可见 ( ) ( 1) , k k+ x x 几乎仅差一个常数 1 ( 1) 1 ( 1) ( ) 1 / + +   k k k v x 所以：  x x 任意分量相除 特征向量乘以任意数， 仍是特征向量

中图科亨技术大空数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS (2)若：2=2>≥.≥2，元1=-元 "a+(少as-会 则k足够大时，有 x≈2*ay+(ya,y) 所以：x2k+2)/x2)≈22 x2k+0/x2k-D≈ 所以：y≈x++x y2≈x+-,x)

数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS （2）若： 1 2 3 1 2  =     n , = − ( )                 = + − + + n n k k k k n x v v  v      1 1 1 1 2 2 ( ) 1  ( ( ) ) 1 1 1 2 2 ( ) x v 1 v k k k    + −  则k足够大时，有 2 1 (2 1) (2 1) 2 1 (2 2) (2 ) / /     + − + k k k k x x 所以： x x ( ) 1 ( 1) 2 ( ) 1 ( 1) 1 k k k k v x x v x x    −  + + + 所以：

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 算法：1、给出初值，计算序列x+)=Ax 2、若序列表现为，相邻两个向量各个分量比趋向于常数 2≈xk+/x) 当≈x) 若序列表现为，奇偶序列各个分量比趋向于常数，则 2≈√xk+D/xk-0 y≈xk++2x) y2≈xk+-2x) 若序列表现为其他，退出不管

数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 算法：1、给出初值，计算序列 (k 1) (k ) x = Ax + 2、若序列表现为，相邻两个向量各个分量比趋向于常数 ( ) 1 ( 1) ( ) 1 / k k k v x x x   +  若序列表现为，奇偶序列各个分量比趋向于常数，则 ( 1) ( 1) 1 ( 1) ( ) 1 1 ( 1) ( ) 2 1 / k k k k k k x x v x x v x x    + − + +   +  − 若序列表现为其他，退出不管

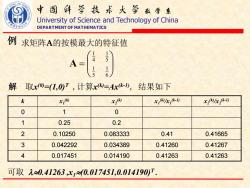
中图科亨技术大学越学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 例求矩阵A的按模最大的特征值 解取x0=1,0T,计算xW=Ak-,结果如下 k x因 x3例 x((k-1) x2(k(k-1) 0 1 0 1 0.25 0.2 3 0.10250 0.083333 0.41 0.41665 3 0.042292 0.034389 0.41260 0.41267 4 0.017451 0.014190 0.41263 0.41263 可取10.41263，x10.017451,0.014190T

数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 求矩阵A的按模最大的特征值 解 取x (0)=(1,0)T ,计算x (k)=Ax(k-1) , 结果如下 例         = 6 1 5 1 5 1 4 1 A k x1 (k) x2 (k) x1 (k)/x1 (k-1) x2 (k)/x2 (k-1) 0 1 0 1 0.25 0.2 2 0.10250 0.083333 0.41 0.41665 3 0.042292 0.034389 0.41260 0.41267 4 0.017451 0.014190 0.41263 0.41263 可取 0.41263 ,x1(0.017451,0.014190)T

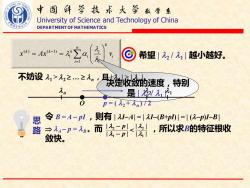
中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS © 希望|22/九1越小越好。 不妨设元>1之.之类定收敛的速度：特别 是」2 0 p=(2+n)f2 思 令B=A-pl,则有I2-A=|2-(B+p山川=|(-p)-B1 路 煎使P=.而冬受，所以求的特征根收 敛快

数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS ( ) ( 1) 1 1 1 k n k k k i i i i x Ax v     − =   = =      决定收敛的速度，特别 是 | 2 / 1 | 希望 | 2 / 1 | 越小越好。 不妨设  1 >  2  .   n，且 |  2 | > |  n |。  n  2  1 O p = (  2 +  n ) / 2 思 路 令 B = A − pI ，则有 | I−A | = | I−(B+pI) | = | (−p)I−B |   A − p =  B。而 ，所以求B的特征根收 敛快。 | | | | | | | | 1 2 1 2      − − p p

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 在幂法中，我们构造的序列 ax 可以看出 .0,121 因此，若序列收敛慢的话，可能造成计算的溢出或归0

数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS                 + +         = + n n k n k k k x v v  v        1 2 2 1 2 1 1 1 ( )  在幂法中，我们构造的序列 可以看出       → + → , 1 0 , 1 , 1 ( ) 1   k k x 因此，若序列收敛慢的话，可能造成计算的溢出或归0