重庆医科大学：《超声治疗学》课程教学课件（讲稿）第一章 质点振动学基础（主讲：樊华）

Haifuo第一章质点振动学基础樊华重庆医科大学生物医学工程系重庆医科大学医学超声工程研究所重庆市-科技部共建超声医学工程重点实验室二〇〇九年八月

第一章 质点振动学基础 樊 华 重庆医科大学生物医学工程系 重庆医科大学医学超声工程研究所 重庆市 -科技部共建超声医学工程重点实验室 二○○ 九年八月

Haifu内容提要>单质点振动系统自由振动★>运动方程及其解>自由振动的能量>单质点的阻尼振动声学之父克拉尼>单质点的强迫振动德国科学家研究板振动力一电一声类比现代声学奠基人瑞利（Rayleigh）（1842-1919)《声的理论》重医科大学

内容提要 Î单质点振动系统 Î自由振动 ★ Î运动方程及其解 Î自由振动的能量 Î单质点的阻尼振动 Î单质点的强迫振动 Î力—电—声类比 声学之父克拉尼 德国科学家 研究板振动 现代声学奠基人瑞利（Rayleigh） （1842-1919） 《声的理论》

Haifuo1．掌握1.1单质点自由振动系统、运动方程及其解，简谐振动、相位和圆频率；1.2位移、速度、加速度与时间的关系；如何根据初始条件确定运动方程；1.3自由振动的能量，动能和势能；1.4振动的复数表示；2.了解2.1单质点阻尼振动2.2力-电-声类比知识3.高等数学知识；4.课后习题

1. 掌握 1.1单质点自由振动系统、运动方程及其解，简谐振 动、相位和圆频率； 1.2位移、速度、加速度与时间的关系；如何根据初始 条件确定运动方程； 1.3 自由振动的能量，动能和势能； 1.4振动的复数表示； 2. 了解 2.1 单质点阻尼振动 2.2 力 - 电 -声类比 3. 知识 高等数学知识； 4. 课后 习题

Haifu一、单质点振动系统>振动与声波的关系？声波是机械波，是机械振动在弹性媒质中的传播。振动是声波的波源（因），声波是振动的传播形式（果重广醫科大学

一、单质点振动系统 Î振动与声波的关系？ 声波是机械波，是 机械振动在弹性媒 质中的传播。 振动是声波的波源 （因），声波是振 动的传播形式（果 ）

Haifu一、单质点振动系统1.1基本概念物理上总可以把物体看作许多质点的组合。>所谓质点振动系统，就是假设构成振动系统的物体如质量块弹簧等，不论其几何大小如何，都可以看成是一个物理性质集中的系统，对于这种系统，质量块的质量认为是集中在一点的，这就是说，构成整个振动系统的质量块与弹簧，它们的运动状态都是均匀的。这种振动系统也称之为理想参数系统。决定一个系统是否为质点振动系统，不是看它的绝对几何尺寸，而是看物体线度与振动产生的声波波长之比。最简单的振动系统应是单质点振动系统。质点：在声学中是指尺度比声波波长小很多的物体的一种简化近视。质点是忽略物质的原子性的。重广醫科大学

1.1 基本概念 一、单质点振动系统 Î物理上总可以把物体看作许多质点的组合。 Î所谓质点振动系统，就是假设构成振动系统的物体如质量块 、弹簧等，不论其几何大小如何，都可以看成是一个物理性质 集中的系统，对于这种系统，质量块的质量认为是集中在一点 的，这就是说，构成整个振动系统的质量块与弹簧，它们的运 动状态都是均匀的。这种振动系统也称之为理想参数系统。 Î决定一个系统是否为质点振动系统，不是看它的绝对几何尺 寸，而是看物体线度与振动产生的声波波长之比。 Î最简单的振动系统应是单质点振动系统。 Î质点：在声学中是指尺度比声波波长小很多的物体的一种简 化近视。 Î质点是忽略物质的原子性的

Haifuo一、单质点振动系统1.2单质点的自由振动1.2.1运动方程及其解M>振动系统原件光滑平面质量块（M）+x0Xo弹簧（弹性系数或者劲单质点自由振动系统度系数k）重广醫科大学

一、单质点振动系统 1.2 单质点的自由振动 1.2.1 运动方程及其解 Î振动系统原件 质量块（ M ） 弹簧（弹性系数或者劲 度系数 k ） k M O x 0 x 光滑平面 单质点自由振动系统

一、单质点振动系统HaifuFk>受力分析FNMV光滑平面+x0Xo弹力F、牛顿力FN单质点自由振动系统力的平衡：Fk=Fn重广科大学

一、单质点振动系统 Î受力分析 弹力 Fk、牛顿力 FN 力的平衡： Fk=F N k M O x 0 x 光滑平面 单质点自由振动系统 FN Fk

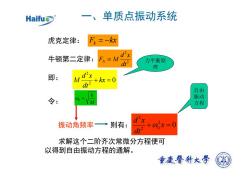
一、单质点振动系统HaifuF=-kx虎克定律：Fi=Md'x牛顿第二定律：力平衡原dt?理d'x即：M+ kx=0dt自由K振动00=VM令：方程d'x+0x=0→则有：振动角频率dt?求解这个二阶齐次常微分方程便可以得到自由振动方程的通解。重广醫科大学

M k ω0 = 一、单质点振动系统 F kx k = − 2 2 dt d x FN = M 0 2 2 + kx = dt d x M 虎克定律： 牛顿第二定律： 即： 力平衡原 理 令： 振动角频率 则有： 自由 振动 方程 求解这个二阶齐次常微分方程便可 以得到自由振动方程的通解。 0 2 2 0 2 + x = dt d x ω

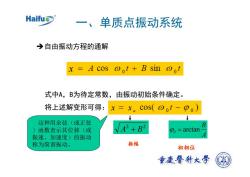
Haifu一、单质点振动系统>自由振动方程的通解x=Acoso。t+Bsinot式中A，B为待定常数，由振动初始条件确定将上述解变形可得：x =x. cos( @ot - P。)这种用余弦（或正弦BVA+B2函数表示其位移（或Po=arctanA振速、加速度）的振动振幅称为简谐振动。初相位重广醫科大学

一、单质点振动系统 Î自由振动方程的通解 2 2 A + B 式中A，B为待定常数，由振动初始条件确定。 将上述解变形可得： 初相位 A B arctan ϕ0 = 振幅 这种用余弦（或正弦 ）函数表示其位移（或 振速、加速度）的振动 称为简谐振动。 x x x a

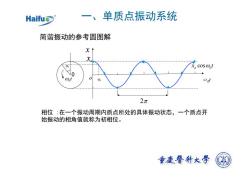
、单质点振动系统Haifu简谐振动的参考圆图解xXcosw.t0O.tQot02元相位：在一个振动周期内质点所处的具体振动状态，一个质点开始振动的相角值就称为初相位。重广醫科大学

ω0t x o xa x t a 0 cosω ϕ0 ϕ0 2π 一、单质点振动系统 简谐振动的参考圆图解 相位 :在一个振动周期内质点所处的具体振动状态，一个质点开 始振动的相角值就称为初相位。 t ω0 0