西安电子科技大学：《纠错码》课程教学资源（课件讲义）Cyclic Codes

Cyclic Codes Yunghsiang S.Han（韩永祥) School of Electrical Engineering Intelligentization Dongguan University of Technology(东莞理工学院) China E-mail:yunghsiangh@gmail.com

Cyclic Codes Yunghsiang S. Han （韩永祥） School of Electrical Engineering & Intelligentization Dongguan University of Technology (东莞理工学院) China E-mail: yunghsiangh@gmail.com

Y.S.Han Cyclic codes Description of Cyclic Codes If the components of an n-tuple v=(vo,v1,...,Un-1)are cyclically shifted i places to the right,the resultant n-tuple would be v）=(n-i,vn-i+1,,vn-l,0,U1,,n-i-1). Cyclically shifting v i places to the right is equivalent to cyclically shifting v n-i places to the left. An (n,k)linear code C is called a cyclic code if every cyclic shift of a code vector in C is also a code vector in C. Code polynomial v(x)of the code vector v is defined as u(x)=0+U1x+…+n-1xn-1. ·v((c)=xv(x)）mod zm+1. School of Electrical Engineering Intelligentization,Dongguan University of Technology

Y. S. Han Cyclic codes 1 Description of Cyclic Codes • If the components of an n-tuple v = (v0, v1, . . . , vn−1) are cyclically shifted i places to the right, the resultant n-tuple would be v (i) = (vn−i , vn−i+1, . . . , vn−1, v0, v1, . . . , vn−i−1). • Cyclically shifting v i places to the right is equivalent to cyclically shifting v n − i places to the left. • An (n, k) linear code C is called a cyclic code if every cyclic shift of a code vector in C is also a code vector in C. • Code polynomial v(x) of the code vector v is defined as v(x) = v0 + v1 x + · · · + vn−1 x n−1 . • v (i) (x) = x i v(x) mod x n + 1. School of Electrical Engineering & Intelligentization, Dongguan University of Technology

Y.S.Han Cyclic codes 2 Proof:Multiplying v(x)by x,we obtain x2v()=0x2+v1x+1+…+n--1xn-1++un-1an+i-1. Then we manipulate the equation into the following form: x2v(x)=n-i+n-i+1x+…+n-1xi-1+0x2+. +n-i-1xn-1+vn-i(xn+1)+wn-i+1x(x”+1) +…+vn-1x2-1(xn+1) =q(x)(xn+1)+v@(c), Where q(x)=Un-i+Un-i+1x+...+Un-1xi-1, The nonzero code polynomial of minimum degree in a cyclic code C is unique. Let g(x)=go+gx+...+gr-1x"-1+z"be the nonzero code polynomial of minimum degree in an (n,k)cyclic code C. Then the constant term go must be equal to 1. School of Electrical Engineering Intelligentization,Dongguan University of Technology

Y. S. Han Cyclic codes 2 Proof: Multiplying v(x) by x i , we obtain x i v(x) = v0 x i + v1 x i+1 + · · · + vn−i−1 x n−1 + · · · + vn−1 x n+i−1 . Then we manipulate the equation into the following form: x i v(x) = vn−i + vn−i+1x + · · · + vn−1 x i−1 + v0 x i + · · · +vn−i−1 x n−1 + vn−i (x n + 1) + vn−i+1x(x n + 1) + · · · + vn−1 x i−1 (x n + 1) = q(x)(x n + 1) + v (i) (x), where q(x) = vn−i + vn−i+1x + · · · + vn−1 x i−1 . • The nonzero code polynomial of minimum degree in a cyclic code C is unique. • Let g(x) = g0 + g1 x + · · · + gr−1 x r−1 + x r be the nonzero code polynomial of minimum degree in an (n, k) cyclic code C. Then the constant term g0 must be equal to 1. School of Electrical Engineering & Intelligentization, Dongguan University of Technology

Y.S.Han Cyclic codes Proof:Suppose that go =0.Then 9(x)=91x+92x2+·+9,-1x-1+x =x(g1+92x+…+9-1x-2+x-1). If we shift g(x)cyclically n-1 places to the right (or one place to the left),we obtain a nonzero code polynomial, g1+g2+...+gr-x"-2+x"-1,which has a degree less than r.Contradiction. School of Electrical Engineering Intelligentization,Dongguan University of Technology

Y. S. Han Cyclic codes 3 Proof: Suppose that g0 = 0. Then g(x) = g1 x + g2 x 2 + · · · + gr−1 x r−1 + x r = x(g1 + g2 x + · · · + gr−1 x r−2 + x r−1 ). If we shift g(x) cyclically n − 1 places to the right (or one place to the left), we obtain a nonzero code polynomial, g1 + g2 x + · · · + gr−1 x r−2 + x r−1 , which has a degree less than r. Contradiction. School of Electrical Engineering & Intelligentization, Dongguan University of Technology

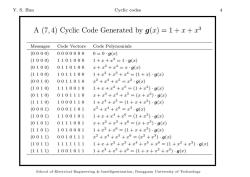
Y.S.Han Cyclic codes A (7,4)Cyclic Code Generated by g(x)=1+x+23 Messages Code Vectors Code Polynomials (0000) 00000000=0·g(x) (1000) 11010001+x+x3=1·g(x) (0100) 0110100x+x2+x4=x·g(x) (1100) 1011100 1+x2+x3+x4=(1+x)·g(x) (0010) 0011010 x2+x3+x5=x2·g(c) (1010) 1110010 1+x+x2+x5=(1+x2)·9(x) (0110) 0101110 x+x3+x4+x5=(x+x2)·g(x) (1110) 1000110 1+x4+x5=(1+x+x2)·g(x) (0001) 0001101 x3+x4+x6=x3·g(c) (1001) 11001011+x+x4+x6=(1+x3)·g(x) (0101) 0111001 x+x2+x3+x6=(x+x3)·g(x) (1101) 1010001 1+x2+x6=(1+x+x3)·g(x) (0011) 0010111x2+x4+x5+x6=(x2+x3)·g(x) (1011) 1111111 1+x+x2+x3+x4+x5+x6=(1+x2+x3)·g(x) (1111) 1001011 1+x3+x5+x6=(1+x+x2+x3)·g(c) School of Electrical Engineering Intelligentization,Dongguan University of Technology

Y. S. Han Cyclic codes 4 A (7, 4) Cyclic Code Generated by g(x) = 1 + x + x 3 Messages Code Vectors Code Polynomials (0 0 0 0) 0 0 0 0 0 0 0 0 = 0 · g(x) (1 0 0 0) 1 1 0 1 0 0 0 1 + x + x 3 = 1 · g(x) (0 1 0 0) 0 1 1 0 1 0 0 x + x 2 + x 4 = x · g(x) (1 1 0 0) 1 0 1 1 1 0 0 1 + x 2 + x 3 + x 4 = (1 + x) · g(x) (0 0 1 0) 0 0 1 1 0 1 0 x 2 + x 3 + x 5 = x 2 · g(x) (1 0 1 0) 1 1 1 0 0 1 0 1 + x + x 2 + x 5 = (1 + x 2 ) · g(x) (0 1 1 0) 0 1 0 1 1 1 0 x + x 3 + x 4 + x 5 = (x + x 2 ) · g(x) (1 1 1 0) 1 0 0 0 1 1 0 1 + x 4 + x 5 = (1 + x + x 2 ) · g(x) (0 0 0 1) 0 0 0 1 1 0 1 x 3 + x 4 + x 6 = x 3 · g(x) (1 0 0 1) 1 1 0 0 1 0 1 1 + x + x 4 + x 6 = (1 + x 3 ) · g(x) (0 1 0 1) 0 1 1 1 0 0 1 x + x 2 + x 3 + x 6 = (x + x 3 ) · g(x) (1 1 0 1) 1 0 1 0 0 0 1 1 + x 2 + x 6 = (1 + x + x 3 ) · g(x) (0 0 1 1) 0 0 1 0 1 1 1 x 2 + x 4 + x 5 + x 6 = (x 2 + x 3 ) · g(x) (1 0 1 1) 1 1 1 1 1 1 1 1 + x + x 2 + x 3 + x 4 + x 5 + x 6 = (1 + x 2 + x 3 ) · g(x) (1 1 1 1) 1 0 0 1 0 1 1 1 + x 3 + x 5 + x 6 = (1 + x + x 2 + x 3 ) · g(x) School of Electrical Engineering & Intelligentization, Dongguan University of Technology

Y.S.Han Cyclic codes Consider the polynomial xg(x),22g(x),...,xm--1g(x). Clearly,they are cyclic shifts of g(x)and hence code polynomials in C.Since C is linear,a linear combination of g(x),xg(x),...,xn-r-1g(x), v(x）=uog(r)+u1xg(）+…+n-r-1an-r-1g(x) =(o+w1x+·+n-r-1xn-T-1)g(x), is also a code polynomial where ui∈{0，l}. Let g(z)=1+gx+...+gr-1x"-1+x"be the nonzero code polynomial of minimum degree in an (n,k)cyclic code C.A binary polynomial of degree n-1 or less is a code polynomial if and only if it is a multiple of g(x). Proof:Let v(x)be a binary polynomial of degree n-1 or less. Suppose that v(x)is a multiple of g(x).Then v(x)=(ao+az+...+an-r-1x"-r-1)g(x) School of Electrical Engineering Intelligentization,Dongguan University of Technology

Y. S. Han Cyclic codes 5 • Consider the polynomial xg(x), x2 g(x), . . . , xn−r−1 g(x). Clearly, they are cyclic shifts of g(x) and hence code polynomials in C. Since C is linear, a linear combination of g(x), xg(x), . . . , xn−r−1 g(x), v(x) = u0 g(x) + u1 xg(x) + · · · + un−r−1 x n−r−1 g(x) = (u0 + u1 x + · · · + un−r−1 x n−r−1 )g(x), is also a code polynomial where ui ∈ {0, 1}. • Let g(x) = 1 + g1 x + · · · + gr−1 x r−1 + x r be the nonzero code polynomial of minimum degree in an (n, k) cyclic code C. A binary polynomial of degree n − 1 or less is a code polynomial if and only if it is a multiple of g(x). Proof: Let v(x) be a binary polynomial of degree n − 1 or less. Suppose that v(x) is a multiple of g(x). Then v(x) = (a0 + a1 x + · · · + an−r−1 x n−r−1 )g(x) School of Electrical Engineering & Intelligentization, Dongguan University of Technology

Y.S.Han Cyclic codes 6 aog(x)+axg(x)+...+an-r-1x"-r-1g(x). Since v(x)is a linear combination of the code polynomials, g(x),xg(x),...,"--1g(x),it is a code polynomial in C. Now let v(x)be a code polynomial in C.Dividing v(x)by g(x),we obtain v(x)=a(x)g(z)+b(x), where the degree of b(x)is less than the degree of g(z).Since v(x)and a(x)g(x)are code polynomials,b(x)is also a code polynomial.Suppose b(x)0.Then b(x)is a code polynomial with less degree than that of g(x).Contradiction. The number of binary polynomials of degree n-1 or less that are multiples of g(x)is 2m-r. There are total of 2 code polynomials in C,2"-=2%,i.e., r=n-k. School of Electrical Engineering Intelligentization,Dongguan University of Technology

Y. S. Han Cyclic codes 6 = a0 g(x) + a1 xg(x) + · · · + an−r−1 x n−r−1 g(x). Since v(x) is a linear combination of the code polynomials, g(x), xg(x), . . . , xn−r−1 g(x), it is a code polynomial in C. Now let v(x) be a code polynomial in C. Dividing v(x) by g(x), we obtain v(x) = a(x)g(x) + b(x), where the degree of b(x) is less than the degree of g(x). Since v(x) and a(x)g(x) are code polynomials, b(x) is also a code polynomial. Suppose b(x) ̸= 0. Then b(x) is a code polynomial with less degree than that of g(x). Contradiction. • The number of binary polynomials of degree n − 1 or less that are multiples of g(x) is 2 n−r . • There are total of 2 k code polynomials in C, 2 n−r = 2k , i.e., r = n − k. School of Electrical Engineering & Intelligentization, Dongguan University of Technology

Y.S.Han Cyclic codes The polynomial g(x)is called the generator polynomial of the code. The degree of g(x)is equal to the number of parity-check digits of the code. The generator polynomial g(x)of an (n,k)cyclic code is a factor of x"+1. Proof:We have xg(x)=(n+1)+g(c). Since g(k)()is the code polynomial obtained by shifting g(x) to the right cyclically k times,g()is a multiple of g(). Hence, 2n+1={xk+a(x)}g(z). If g(x)is a polynomial of degree n-k and is a factor of x"+1, then g(x)generates an (n,k)cyclic code. School of Electrical Engineering Intelligentization,Dongguan University of Technology

Y. S. Han Cyclic codes 7 • The polynomial g(x) is called the generator polynomial of the code. • The degree of g(x) is equal to the number of parity-check digits of the code. • The generator polynomial g(x) of an (n, k) cyclic code is a factor of x n + 1. Proof: We have x k g(x) = (x n + 1) + g (k) (x). Since g (k) (x) is the code polynomial obtained by shifting g(x) to the right cyclically k times, g (k) (x) is a multiple of g(x). Hence, x n + 1 = {x k + a(x)}g(x). • If g(x) is a polynomial of degree n − k and is a factor of x n + 1, then g(x) generates an (n, k) cyclic code. School of Electrical Engineering & Intelligentization, Dongguan University of Technology

Y.S.Han Cyclic codes 8 Proof:A linear combination of g(),xg(a),...g(), v(x)=aog(x)+alzg(x)+...+ak-1xk-1g(z) =(a0+a1x+·+ak-1x-1)g(x), is a polynomial of degree n-1 or less and is a multiple of g(x). There are a total of 2%such polynomial and they form an (n,k) linear code. Let v(x)=vo +v12+...+Un-1x"-1 be a code polynomial in this code.We have xv(c)=0x+u1x2+…+n-1x” =vn-1(x”+1)+(n-1+0x+…+vn-2xn-1) =vn-1(xn+1)+v1(c). Since both xu(x)and x"+1 are divisible by g(a),v(1)must be divisible by g().Hence,v(1)(x)is a code polynomial and the code generated by g()is a cyclic code. School of Electrical Engineering Intelligentization,Dongguan University of Technology

Y. S. Han Cyclic codes 8 Proof: A linear combination of g(x), xg(x), . . . , xk−1 g(x), v(x) = a0 g(x) + a1 xg(x) + · · · + ak−1 x k−1 g(x) = (a0 + a1 x + · · · + ak−1 x k−1 )g(x), is a polynomial of degree n − 1 or less and is a multiple of g(x). There are a total of 2 k such polynomial and they form an (n, k) linear code. Let v(x) = v0 + v1 x + · · · + vn−1 x n−1 be a code polynomial in this code. We have xv(x) = v0 x + v1 x 2 + · · · + vn−1 x n = vn−1(x n + 1) + (vn−1 + v0 x + · · · + vn−2 x n−1 ) = vn−1 (x n + 1) + v (1)(x). Since both xv(x) and x n + 1 are divisible by g(x), v (1) must be divisible by g(x). Hence, v (1)(x) is a code polynomial and the code generated by g(x) is a cyclic code. School of Electrical Engineering & Intelligentization, Dongguan University of Technology

Y.S.Han Cyclic codes Suppose that the message to be encoded is u=(uo,u1,...,uk-1).Then xn-ku(c)=uoxn-k+u1xn-k+1+…十uk-1xn-1. Dividing z-ku(x)by g(x),we have x"-ku(x)=a(x)g(z)+b(x). Since the degree of g(x)is n-k,the degree of b(x)must be n-k-1 or less.Then b(x)+x"-ku(x)=a(x)g(x) is a multiple of g(x)and therefore it is a code polynomial. b(c）+xn-u(c）=b0+b1x+…+bn-k-1xn-k-1 +uoxn-k+u1x”-k+1+…+-1xn-1 School of Electrical Engineering Intelligentization,Dongguan University of Technology

Y. S. Han Cyclic codes 9 • Suppose that the message to be encoded is u = (u0, u1, . . . , uk−1). Then x n−k u(x) = u0 x n−k + u1 x n−k+1 + · · · + uk−1 x n−1 . Dividing x n−k u(x) by g(x), we have x n−k u(x) = a(x)g(x) + b(x). Since the degree of g(x) is n − k, the degree of b(x) must be n − k − 1 or less. Then b(x) + x n−k u(x) = a(x)g(x) is a multiple of g(x) and therefore it is a code polynomial. b(x) + x n−k u(x) = b0 + b1 x + · · · + bn−k−1 x n−k−1 +u0 x n−k + u1 x n−k+1 + · · · + uk−1 x n−1 School of Electrical Engineering & Intelligentization, Dongguan University of Technology