中国科学技术大学:《数字逻辑电路》课程教学资源(课件讲稿)第二章 逻辑代数基础

中国辩学我术大学 University of Science and Technology of China 第二章逻辑代数基础 本章目录 >2.1概述 >2.2逻辑代数中的三种基本运算 >2.3逻辑代数的基本公式和常用公式 >2.4逻辑代数的基本定理 >2.5逻辑函数及其描述方法 >2.6逻辑函数的化简方法 >2.7具有无关项的逻辑函数及其化简 >2.8多输出逻辑函数的化简 >2.9逻辑函数形式的变换 2017-8-4 第二章逻辑代数基础 §2.1概述 基本概念 >逻辑:事物的因果关系。 >逻辑代数:是描述客观事物逻辑关系的数学方法,是进行逻 辑分析与逻辑综合的数学工具。 >逻辑变量:逻辑代数中的变量。逻辑变量的取值范围仅为 0”和“1”,且无大小、正负之分。 >逻辑运算:逻辑变量按照指定的某种因果关系进行推理运算 的过程。 算术运算 普通代数(加减乘除) 逻辑运算 一布尔代数 (与或非等) 2017-8-4 第二章逻辑代数基础 2
2017-8-4 第二章 逻辑代数基础 1 第二章 逻辑代数基础 第二章 逻辑代数基础 本章目录 ¾2.1 概述 ¾2.2 逻辑代数中的三种基本运算 ¾2.3 逻辑代数的基本公式和常用公式 ¾2.4 逻辑代数的基本定理 ¾2.5 逻辑函数及其描述方法 ¾2.6 逻辑函数的化简方法 ¾2.7 具有无关项的逻辑函数及其化简 ¾2.8 多输出逻辑函数的化简 ¾2.9 逻辑函数形式的变换 2017-8-4 第二章 逻辑代数基础 2 基本概念 ¾ 逻辑:事物的因果关系。 ¾ 逻辑代数:是描述客观事物逻辑关系的数学方法,是进行逻 辑分析与逻辑综合的数学工具。 ¾ 逻辑变量:逻辑代数中的变量。逻辑变量的取值范围仅为 “0”和“1”,且无大小、正负之分。 ¾ 逻辑运算:逻辑变量按照指定的某种因果关系进行推理运算 的过程。 §2.1 概述 算术运算——普通代数(加减乘除) 逻辑运算——布尔代数(与或非等)

§2.2逻辑代数中的三种基本运算 逻辑代数的基本运算有与(AND)、或(OR)、非NOT)三种。 (a) (b) (c) 三种电路的因果关系不同。 2017-8-4 第二章逻辑代数基础 §2.2逻辑代数中的三种基本运算 与运算:只有决定事物结果的条件同时具备时,结果才发生。 开关A 开关B 灯Y A B 断开 断开 不亮 0 0 0 断开 闭合 不亮 0 1 0 闭合 断开 不亮 1 0 0 闭合 闭合 亮 1 1 1 以A=1表示开关A闭合,A=0表示开关A断开; 以B=1表示开关B闭合,B=0表示开关B断开; 以=1表示灯亮,Y=0表示灯不亮。 2017-8-4 第二章逻辑代数基础
2017-8-4 第二章 逻辑代数基础 3 §2.2 逻辑代数中的三种基本运算 逻辑代数的基本运算有与(AND)、或(OR)、非(NOT)三种。 三种电路的因果关系不同。 2017-8-4 第二章 逻辑代数基础 4 §2.2 逻辑代数中的三种基本运算 与运算:只有决定事物结果的条件同时具备时,结果才发生。 闭合 闭合 亮 闭合 断开 不亮 断开 闭合 不亮 断开 断开 不亮 开关A 开关B 灯Y 1 1 1 1 0 0 0 1 0 0 0 0 A B Y 以A=1表示开关A闭合,A=0表示开关A断开; 以B=1表示开关B闭合,B=0表示开关B断开; 以Y=1表示灯亮,Y=0表示灯不亮

§2.2逻辑代数中的三种基本运算 与运算:只有决定事物结果的条件同时具备时,结果才发生。 B A、 .Y B 与 -Y A B P 0 0 0 运算规则: 一般形式: 0 1 0 00=0 0A=0 1 0 0 0.1=0 1·A=A 1 1 1 1.0=0 A·A=A Y=AB=AB 1.1=1 2017-8-4 第二章逻辑代数基础 §2.2逻辑代数中的三种基本运算 或运算:在决定事物结果的诸条件中只要有任何一个满足,结 果就会发生。 B 或 AD-Y A B Y 0 0 0 运算规则: 一般形式: 0 1 1 0+0=0 0+A=A 1 0 0+1=1 1+A=1 1 1 1 1+0=1 A+A=A Y=A+B 1+1=1 2017-8-4 第二章逻辑代数基础 6
2017-8-4 第二章 逻辑代数基础 5 1 1 1 1 0 0 0 1 0 0 0 0 A B Y §2.2 逻辑代数中的三种基本运算 与运算:只有决定事物结果的条件同时具备时,结果才发生。 Y=A·B=AB 1 1 1 1 0 0 0 1 0 0 0 0 ⋅ = ⋅ = ⋅ = ⋅ = 运算规则: 一般形式: A A A A A A ⋅ = ⋅ = ⋅ = 1 0 0 2017-8-4 第二章 逻辑代数基础 6 1 1 1 1 0 1 0 1 1 0 0 0 A B Y §2.2 逻辑代数中的三种基本运算 或运算:在决定事物结果的诸条件中只要有任何一个满足,结 果就会发生。 Y = A+B 1 1 1 1 0 1 0 1 1 0 0 0 + = + = + = + = 运算规则: 一般形式: A A A A A A + = + = + = 1 1 0

§2.2逻辑代数中的三种基本运算 非运算:只要条件具备了,结果便不会发生;而条件不具备时, 结果一定发生。 非 A 0 1 运算规则: 一般形式: 1 0 0'=1 (A)'=A Y=A'=A 1'=0 A.4=0 A+A=1 2017-8-4 第二章逻辑代数基础 §2.2逻辑代数中的三种基本运算 几种常用的复合逻辑运算:与非、或非、与或非、异或、同或。 ●与非 A B 00 1 01 1 10 1 与非 11 0 Y=(4-B)' ●或非 A B Y 0 0 1 01 0 10 0 或非 11 0 Y=(A+B)' 2017-8-4 第二章逻辑代数基础 8
2017-8-4 第二章 逻辑代数基础 7 1 0 0 1 A Y §2.2 逻辑代数中的三种基本运算 Y = A′ = A 非运算:只要条件具备了,结果便不会发生;而条件不具备时, 结果一定发生。 1' 0 0' 1 = = 运算规则: 一般形式: ' 1 ' 0 ( ')' + = ⋅ = = A A A A A A 2017-8-4 第二章 逻辑代数基础 8 z 与非 §2.2 逻辑代数中的三种基本运算 1 1 0 1 0 1 0 1 1 0 0 1 A B Y 1 1 0 1 0 0 0 1 0 0 0 1 A B Y z 或非 几种常用的复合逻辑运算:与非、或非、与或非、异或、同或

§2.2逻辑代数中的三种基本运算 几种常用的复合逻辑运算:与非、或非、与或非、异或、同或。 ●与或非 ABCD ABCD 0000 1000 0001 1 1001 1 0010 1010 1 0011 0 1011 0 0100 1100 0 B 0101 1 1101 0 D 0110 1110 0 与或非 0111 0 1111 0 Y=(A·B+C·D)Y 2017-8-4 第二章逻辑代数基础 9 §2.2逻辑代数中的三种基本运算 几种常用的复合逻辑运算:与非、或非、与或非、异或、同或。 ·异或 A B =1 B 0 0 0 异或 Y=A⊕B=AB'+A'B 0 1 1 1 0 1 AD-y 1 1 0 Y=A⊕B ·同或 0 0 1 同或 Y=A⊙B=AB+AB 0 1 0 1 0 0 Y A⊕B=(A⊙B)Y 1 1 1 A⊙B=(A⊕B) Y=A⊙B 2017-8-4 第二章逻辑代数基础 10
2017-8-4 第二章 逻辑代数基础 9 z 与或非 §2.2 逻辑代数中的三种基本运算 0111 0 1111 0 0110 1 1110 0 0101 1 1101 0 0100 1 1100 0 0011 0 1011 0 0010 1 1010 1 0001 1 1001 1 0000 1 1000 1 ABCD Y ABCD Y 几种常用的复合逻辑运算:与非、或非、与或非、异或、同或。 2017-8-4 第二章 逻辑代数基础 10 z 异或 1 1 0 1 0 1 0 1 1 0 0 0 A B Y §2.2 逻辑代数中的三种基本运算 z 同或 1 1 1 1 0 0 0 1 0 0 0 1 A B Y 几种常用的复合逻辑运算:与非、或非、与或非、异或、同或。 Y = A⊕ B = AB′ + A′B Y = A⊙B = AB + A′B′ A⊙B = (A⊕ B)′ A⊕ B = (A⊙B)′
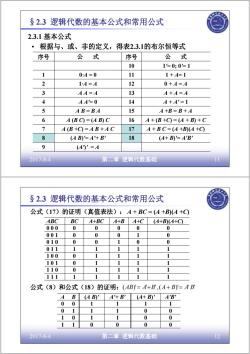
§2.3逻辑代数的基本公式和常用公式 2.3.1基本公式 。根据与、或、非的定义, 得表2.3.1的布尔恒等式 序号 公式 序号 公 式 10 1=0;0=1 1 0A=0 11 1+A=1 2 1A=A 12 0+A=A 3 AA-A 13 A+A=A 4 A4-0 14 A+A'=1 5 AB=BA 15 A+B=B+A 6 A(B C)=(AB)C 16 A+(B+C)=(A+B)+C 7 A(B+C)=AB+AC 17 A+BC=(A+B)(A+C) 8 (AB)=A+B' 18 (A+B)=A'B' 9 (A)'=A 2017-8-4 第二章逻辑代数基础 §2.3 逻辑代数的基本公式和常用公式 公式(17)的证明 (真值表法):A+BC=(A+B)(A+C ABC BC A+BC 4+B A+C (A+B)(A+C) 000 0 0 0 0 0 001 0 0 0 1 0 010 0 0 1 0 0 011 1 1 1 1 1 100 0 1 1 1 1 101 0 1 1 1 1 110 0 1 1 1 1 111 1 1 1 1 1 公式(8) 和公式(18) 的证明:(AB)=A+B,(A+B)=B A B (AB)' A'+B' (A+B)' A'B' 0 0 1 1 1 1 0 1 1 1 0 0 1 0 1 1 0 0 1 1 0 0 0 0 2017-8-4 第二章逻辑代数基础 12
2017-8-4 第二章 逻辑代数基础 11 • 根据与、或、非的定义,得表2.3.1的布尔恒等式 9 (A')' = A 8 (A B)'= A'+ B' 18 (A+ B)'= A'B' 7 A (B +C) = A B + A C 17 A + B C = (A +B)(A +C) 6 A (B C) = (A B) C 16 A + (B +C) = (A + B) + C 5 A B = B A 15 A +B = B + A 4 A A'= 0 14 A + A' = 1 3 A A = A 13 A + A = A 2 1·A = A 12 0 + A = A 1 0·A = 0 11 1 + A= 1 10 1'= 0; 0'= 1 序号 公 式 序号 公 式 §2.3 逻辑代数的基本公式和常用公式 2.3.1 基本公式 2017-8-4 第二章 逻辑代数基础 12 公式(17)的证明(真值表法): 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 1 0 1 1 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 ABC BC A+BC A+B A+C (A+B)(A+C) §2.3 逻辑代数的基本公式和常用公式 A + BC = (A +B)(A +C) 公式(8)和公式(18)的证明:(AB)'= A'+B',(A+ B)'= A'B' 1 1 0 0 0 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 1 1 1 1 A B (A B)' A'+ B' (A+ B)' A'B

§2.3逻辑代数的基本公式和常用公式 2.3.2若干常用公式 序号 公 式 21 A+AB=A 22 A+A'B=A+B 23 AB+AB'=A 24 A(A+B)=A AB+A'C+BC=AB+AC 25 AB+A'C+BCD=AB+A'C 26 A(AB)=AB';A(AB)=A' 2017-8-4 第二章逻辑代数基础 13 §2.4逻辑代数的基本定理 2.4.1代入定理 在任何一个包含变量A的逻辑等式中,若以另外一个逻辑式取 代式中所有A的位置,则等式仍然成立。 例1:基本公式(17) A+BC=(A+B)(A+C用C.D取代C A+B(CD)=(A+B)(A+CD) =(A+B)(A+C)(A+D) 例2:基本公式(18) (A+B)'=A'.B' 用(B+C)取代B (A+(B+C))'=A'.(B+C)=4'.B'.C" 2017-8-4 第二章逻辑代数基础 14
2017-8-4 第二章 逻辑代数基础 13 26 A (AB)'= AB' ; A'(AB)'= A' A B + A'C + B C = A B + A'C A B + A'C + B CD = A B + A'C 25 24 A ( A + B) = A 23 A B + A B' = A 22 A +A'B = A + B 21 A + A B = A 序 号 公 式 §2.3 逻辑代数的基本公式和常用公式 2.3.2 若干常用公式 2017-8-4 第二章 逻辑代数基础 14 §2.4 逻辑代数的基本定理 2.4.1 代入定理 在任何一个包含变量A的逻辑等式中,若以另外一个逻辑式取 代式中所有A的位置,则等式仍然成立。 例2:基本公式(18) (A+ B)′ = A′⋅ B′ 用(B +C)取代B ⇒ (A+ (B +C))′ = A′⋅(B +C)′ = A′⋅ B′⋅C′ 例1:基本公式(17) = (A+B)(A+C)(A+D) A+BC= (A+B)(A+C) A+B(CD) = (A+B)(A+CD) 用C ⋅ D取代C

§2.4逻辑代数的基本定理 2.4.2反演定理 对于任意一个逻辑式Y,若将其中所有的“换成“+”,“+”换 成“”,0换成1,1换成0,原变量换成反变量,反变量换成原 变量,则得到的结果就是Y'。 注意: (1)需遵守“先括号、然后乘、最后加”的运算优先次序。 (2)不属于单个变量上的反号应保留不变。 例1:Y=A(B+C)+CD Y'=(A'+B'C)(C'+D) =A'C+B'C+A'D'+B'C'D'=A'C+B'C'+AD' 例2:Y=(AB'+Cy+DY+C Y'=((A'+B)C)D)'C 2017-8-4 第二章逻辑代数基础 §2.4逻辑代数的基本定理 2.4.3对偶定理 若两逻辑式相等,则它们的对偶式也相等。 对偶式:对于任意一个逻辑式Y,若将其中所有的“”换成 “+”,“+”换成”,0换成1,1换成0,则得到一个新的逻辑式 D,这个D就称为Y的对偶式。 例1:Y=AB+(C+D)Y Y=(A+B)(CD) 例2:证明表2.3.1中的式(17)A+BC=(A+B)A+C 证明:写出等式两边的对偶式 A(B+C)=AB+AC 2017-8-4 第二章逻辑代数基础 16
2017-8-4 第二章 逻辑代数基础 15 §2.4 逻辑代数的基本定理 2.4.2 反演定理 对于任意一个逻辑式Y,若将其中所有的“·”换成“+”,“+”换 成“·” ,0换成1,1换成0,原变量换成反变量,反变量换成原 变量,则得到的结果就是Y ′ 。 注意: (1)需遵守“先括号、然后乘、最后加”的运算优先次序。 (2)不属于单个变量上的反号应保留不变。 例1:Y = A(B +C) +CD A C B C A D B C D A C B C A D Y' A B C C D = ′ ′ + ′ ′ + ′ ′ + ′ ′ ′ = ′ ′ + ′ ′ + ′ ′ = ′ + ′ ′ ′ + ′ ( )( ) 例2:Y = ((AB' +C)' + D)' +C Y' = (((A' + B)C')'D')'C' 2017-8-4 第二章 逻辑代数基础 16 §2.4 逻辑代数的基本定理 2.4.3 对偶定理 对偶式:对于任意一个逻辑式Y,若将其中所有的“·”换成 “+”,“+”换成“·” ,0换成1,1换成0,则得到一个新的逻辑式 YD ,这个YD就称为Y的对偶式。 例1: 例2:证明表2.3.1中的式(17)A+BC= (A+B)(A+C) 若两逻辑式相等,则它们的对偶式也相等。 Y = AB + (C + D)' Y A B CD ' D = ( + )( ) 证明:写出等式两边的对偶式 A(B+C)=AB+AC

§2.5逻辑函数及其描述方法 2.5.1逻辑函数 描述输入逻辑变量与输出逻辑变量之间因果关系的函数, 写作:Y=FA,B,C,) 注:在二值逻辑中,输入输出都只有两种取值0/1。 例:举重裁判电路 若以1表示开关闭合,0表示开 关断开;以1表示灯亮,0表示 灯暗;则指示灯Y是开关A、 B、C的二值逻辑函数,即 Y=F(A,B,C) 2017-8-4 第二章逻辑代数基础 §2.5逻辑函数及其描述方法 2.5.2逻辑函数的描述方法 一、常用的逻辑函数的描述方法 逻辑真值表、逻辑函数式、逻辑图、波形图、卡诺图和硬件 描述语言。 逻辑真值表:输入逻辑变量所有可能的取值组合与对应的输 出逻辑函数值构成的表格。 逻辑函数式:用与、或、非等运算组合起来,表示逻辑函数 的输出与输入逻辑变量之间关系的逻辑代数式。 逻辑图:用与、或、非等逻辑符号表示输出与输入之间逻辑 关系的图形。 波形图:将输入变量所有可能的取值组合与对应的输出按时 间顺序依次排列起来画成的时间波形。 2017-8-4 第二章逻辑代数基础 18
2017-8-4 第二章 逻辑代数基础 17 §2.5 逻辑函数及其描述方法 2.5.1 逻辑函数 Y=F(A,B,C,······) 描述输入逻辑变量与输出逻辑变量之间因果关系的函数, 写作: 注:在二值逻辑中,输入/输出都只有两种取值0/1。 例:举重裁判电路 若以1表示开关闭合,0表示开 关断开;以1表示灯亮,0表示 灯暗;则指示灯 Y 是开关A、 B、C的二值逻辑函数,即 Y=F(A,B,C) 2017-8-4 第二章 逻辑代数基础 18 2.5.2 逻辑函数的描述方法 逻辑真值表、逻辑函数式、逻辑图、波形图、卡诺图和硬件 描述语言。 一、常用的逻辑函数的描述方法 逻辑真值表:输入逻辑变量所有可能的取值组合与对应的输 出逻辑函数值构成的表格。 逻辑函数式:用与、或、非等运算组合起来,表示逻辑函数 的输出与输入逻辑变量之间关系的逻辑代数式。 逻辑图:用与、或、非等逻辑符号表示输出与输入之间逻辑 关系的图形。 波形图:将输入变量所有可能的取值组合与对应的输出按时 间顺序依次排列起来画成的时间波形。 §2.5 逻辑函数及其描述方法
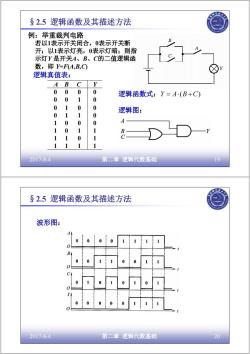
§2.5逻辑函数及其描述方法 例:举重裁判电路 若以1表示开关闭合,0表示开关断 B 开;以1表示灯亮,0表示灯暗;则指 示灯Y是开关A、B、C的二值逻辑函 数,即Y=FA,B,C 逻辑真值表: A B C Y 0 0 0 0 逻辑函数式:Y=A(B+C) 00 1 0 01 0 0 逻辑图: 0 1 1 0 1 0 0 0 A 1 0 1 1 B 1 1 0 1 1 2017-8-4 第二章逻辑代数基础 19 §2.5逻辑函数及其描述方法 波形图: A 00 1 B C 0 2017-8-4 第二章逻辑代数基础 20
2017-8-4 第二章 逻辑代数基础 19 例:举重裁判电路 若以1表示开关闭合,0表示开关断 开;以1表示灯亮,0表示灯暗;则指 示灯Y 是开关A、B、C的二值逻辑函 数,即 Y=F(A,B,C) 1 1 1 1 1 1 0 1 1 0 1 1 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 A B C Y 逻辑真值表: 逻辑函数式:Y = A⋅(B +C) 逻辑图: §2.5 逻辑函数及其描述方法 2017-8-4 第二章 逻辑代数基础 20 波形图: §2.5 逻辑函数及其描述方法
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 中国科学技术大学:《数字逻辑电路》课程教学资源(课件讲稿)第一章 数制和码制.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(课件讲稿)绪论(主讲:胡新伟).pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(实验课件)编码器和译码器.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(实验课件)计数器及其应用——电子秒表.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(实验课件)抢答器.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(实验课件)全加器实验.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(实验课件)数据选择器.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(实验课件)移位寄存器.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(实验课件)数字钟.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(实验课件)数字逻辑电路实验讲义(图片版).pdf
- 中国科学技术大学:《超大规模集成电路设计(VLSI)》课程教学资源(课件讲稿)第12章 CMOS VLSI运算电路.pdf
- 中国科学技术大学:《超大规模集成电路设计(VLSI)》课程教学资源(课件讲稿)第11章 常用的VLSI系统部件.pdf
- 中国科学技术大学:《超大规模集成电路设计(VLSI)》课程教学资源(课件讲稿)第9章 CMOS逻辑电路的高级技术.pdf
- 中国科学技术大学:《超大规模集成电路设计(VLSI)》课程教学资源(课件讲稿)第8章 高速CMOS逻辑电路设计.pdf
- 中国科学技术大学:《超大规模集成电路设计(VLSI)》课程教学资源(课件讲稿)第7章 CMOS逻辑门电子学分析.pdf
- 中国科学技术大学:《超大规模集成电路设计(VLSI)》课程教学资源(课件讲稿)第6章 MOSFET的电气特性.pdf
- 中国科学技术大学:《超大规模集成电路设计(VLSI)》课程教学资源(课件讲稿)第5章 物理设计的基本要素.pdf
- 中国科学技术大学:《超大规模集成电路设计(VLSI)》课程教学资源(课件讲稿)第4章 CMOS集成电路的制造.pdf
- 中国科学技术大学:《超大规模集成电路设计(VLSI)》课程教学资源(课件讲稿)第3章 CMOS集成电路的物理结构.pdf
- 中国科学技术大学:《超大规模集成电路设计(VLSI)》课程教学资源(课件讲稿)第2章 MOSFET逻辑设计.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(课件讲稿)第三章 门电路.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(课件讲稿)第四章 组合逻辑电路.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(课件讲稿)第五章 半导体存储电路.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(课件讲稿)第六章 时序逻辑电路.pdf
- 中国科学技术大学:《数字逻辑电路》课程教学资源(课件讲稿)第七章 脉冲波形的产生和整形电路.pdf
- 合肥工业大学:《数字电子技术基础》课程教学资源(课件讲稿)序言(主讲:梁华国、黄正峰).pdf
- 合肥工业大学:《数字电子技术基础》课程教学资源(课件讲稿)第一章 数制与编码(不同数制间的转换).pdf
- 合肥工业大学:《数字电子技术基础》课程教学资源(课件讲稿)第一章 数制与编码(二进制编码).pdf
- 合肥工业大学:《数字电子技术基础》课程教学资源(课件讲稿)第二章 逻辑代数基础(概述、逻辑代数中的三种基本运算).pdf
- 合肥工业大学:《数字电子技术基础》课程教学资源(课件讲稿)第二章 逻辑代数基础(基本公式、常用公式、基本定理).pdf
- 合肥工业大学:《数字电子技术基础》课程教学资源(课件讲稿)第二章 逻辑代数基础(逻辑函数的化简方法、具有无关项的逻辑函数及其化简).pdf
- 合肥工业大学:《数字电子技术基础》课程教学资源(课件讲稿)第三章 门电路.pdf
- 合肥工业大学:《数字电子技术基础》课程教学资源(课件讲稿)第四章 组合逻辑电路.pdf
- 合肥工业大学:《数字电子技术基础》课程教学资源(课件讲稿)第五章 触发器.pdf
- 合肥工业大学:《数字电子技术基础》课程教学资源(课件讲稿)第六章 时序逻辑电路.pdf
- 合肥工业大学:《数字电子技术基础》课程教学资源(课件讲稿)第七章 半导体存储器.pdf
- 烟台理工学院:《数字电路与逻辑设计》课程教学资源(课件讲稿)第一章 逻辑代数与EDA技术的基础知识(1/4)1.0 概述.pdf
- 烟台理工学院:《数字电路与逻辑设计》课程教学资源(课件讲稿)第一章 逻辑代数与EDA技术的基础知识(2/4)1.1 基本概念、公式和定理.pdf
- 烟台理工学院:《数字电路与逻辑设计》课程教学资源(课件讲稿)第一章 逻辑代数与EDA技术的基础知识(3/4)1. 2 逻辑函数的化简方法.pdf
- 烟台理工学院:《数字电路与逻辑设计》课程教学资源(课件讲稿)第一章 逻辑代数与EDA技术的基础知识(4/4)1.3 逻辑函数的表示方法及其相互之间的转换.pdf
