上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[04]Lecture32-LT and ODEs in class 拉普拉氏变换求解微分方程
ME369-系统模型、分折与控制 3.2拉普拉氏变换求解微分方程 →拉普拉氏求解系统时域响应 *线性时不变微分方程 (linear,time-invariant differential equation) School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 LT法求解常微分方程 +初始条件(Initial condition,IC) 时域模型 频域模型 (时间自变量的微分方程) (s自变量的代数方程) 代数求解 (algebra) 微积分求解 (calculus) 频域解Y(s) ILT 时域解y(⑨ School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 1
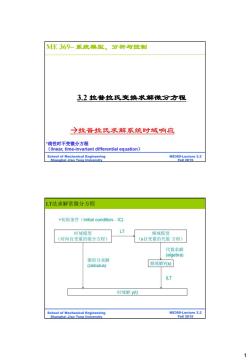
1 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 3.2 拉普拉氏变换求解微分方程 *线性时不变微分方程 (linear, time-invariant differential equation) 拉普拉氏求解系统时域响应 ME 369– 系统模型、分析与控制 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University LT法求解常微分方程 +初始条件(Initial condition,IC) 时域模型 (时间自变量的微分方程) 频域模型 (s自变量的代数 方程) 频域解Y(s) 代数求解 (algebra) 微积分求解 (calculus) ILT LT 时域解 y(t)

[例) 4x+y=10 x(0)=0 求 x(t) 已知 -x+3y+2y=0 y(0)=5 y(t) School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 阶系统(First order system)的自由响应(free response) tr+x=0,x(0)= School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 2
2 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1] 4 10 3 2 0 x y x y y (0) 0 (0) 5 x y () () xt yt , 已知 求 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 一阶系统(First order system)的自由响应(free response) 0 x x x x 0, (0)

阶系统的阶跃响应(step response) tx+x=K,x(0)=Xp School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 阶系统(Sencond order system)的自由响应((free response) +6x+25x=0,x(0)=1,(0)=-3 School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 3
3 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 0 x x K x x , (0) 一阶系统的阶跃响应(step response) BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University x x x x x 6 25 0, (0) 1, (0) 3 二阶系统(Sencond order system)的自由响应(free response)

阶系统的阶跃响应 二 求+6x+25x=1+25u,x(0)=1,x(0)=-3 School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 阶系统的阶跃响应(续) School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 4
4 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University x x x u u x x 6 25 25 , (0) 1, (0) 3 二阶系统的阶跃响应 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 二阶系统的阶跃响应(续)
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[04]Lecture31-LT Definition-in class 拉普拉氏变换——定义及性质.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[04]Lecture30-why in class 拉普拉氏变换——引子及预备.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[03]HW1_homework01_solution.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[03]HW1_homework01.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[02]Lecture23-Modeling Form 模型形式.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[02]Lecture23-Modeling Form 模型形式.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[02]Lecture22-Rotational Mechanical system 转动机械系统建模.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[02]Lecture22-Rotational Mechanical system 转动机械系统建模.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[02]Lecture21-Translational Mechanical system 平动机械系统建模.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[02]Lecture2.1 平动机械系统建模 Translational Mechanical system.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[01]自动控制的故事(简).pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[01]汽车控制.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[01]习题册.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[01]Syllabus(A 类).pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[01]Lecture1-introduction.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[01]Lecture1-introduction(莫锦秋).pdf
- 上海交通大学:《机电伺服元件及系统》课程教学资源(讲义)00 机电控制系统总复习.pdf
- 上海交通大学:《机电伺服元件及系统》课程教学资源(讲义)05 液压伺服系统.pdf
- 上海交通大学:《机电伺服元件及系统》课程教学资源(讲义)04 液压伺服元件.pdf
- 上海交通大学:《机电伺服元件及系统》课程教学资源(讲义)03 电机功率驱动与系统.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[05]Lecture41-Transfer function 传递函数.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[05]Lecture42-block diagram models 方块图.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[05]Lecture43-signal flow graph models 信号流图.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[05]Lecture44-system Transfer function 系统传递函数.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[05]Lecture45-system Model with Matlab 系统模型Matlab表达.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[06]HW2_homework02.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[06]HW2_homework02_solution.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[07]Lecture51-electrical system 电气系统建模.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[07]Lecture52-electroMechanical system 机电系统建模.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[07]Lecture53-lineariztion of nonlinear mathematical models 非线性数字模型的线性化.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[08]Lecture61-Transient and Steady-state Response 瞬态响应和稳态响应.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[08]Lecture62-Stability 系统稳定性.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[08]Lecture63-Steady state error 稳态误差.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[08]Lecture64-Forced response 系统强迫响应.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[08]Lecture65-Free Response 系统自由响应.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[09]HW3_homework03.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[10]HW4_homework04-solution.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[10]HW4_homework04.pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[11]模型分析与控制2014期中试题与答案(草).pdf
- 上海交通大学:《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[12]期中考试2013 -答案.pdf
