西安电子科技大学：《高等数学》课程PPT教学课件（讲稿）第一章 函数与极限 1.6 极限存在准则、两个重要极限

西安毛子科技大学数学与统计学院Schoolofmathematies and statistiesXIDIAN UNIVERSITY高等数学极限存在准则两个重要极限

极限存在准则 两个重要极限

西要毛子科技大学极限存在准则，两个重要极限XIDIANUNIVERSITY、准则I及重要极限1.准则I如果数列(x,(y/及(zn)满足条件：yn ≤x, ≤zn (n>no,neN );(1)lim yn =limzn, = a,(2)n->00n->olimx, = a.则n-00称这个准则为夹逼准则

极限存在准则，两个重要极限 一、 准则Ⅰ及重要极限 1. 准则Ⅰ 如果数列 x y n n ,  及 z n 满足条件： (1) 0 0 ( , N ); n n n   lim lim , n n n n y z a → → （2） = = 称这个准则为夹逼准则 lim . n n x a → 则 = n n n y x z  

西安毛子科技大学极限存在准则，两个重要极限XIDIAN UNIVERSITS(1)yn≤xn≤zn，(2) limy,=limz,=α证由条件（2）ε>0，正整数N，N当n>N,时,ly,-akiα-N,时,n-aa-N时，有a-<yn≤,≤z<a+→x,-ak,则lim=a条件（1)

极限存在准则，两个重要极限 证 由条件（2） , n n n （1） y x z   lim lim n n n n y z a → → （2） = =    0, n 当 y a −   n N 1 时， n  −   + a y a   n 当 z a −   n N 2 时， n  −   + a z a   取 N n N N = max , ,  0 1 2 a a −   y z n n  + ，当 n N 时， , n x a −   则 lim n n x a → = 条件（1）   n x 1 N2  正整数 N , 有

西要毛子科技大学极限存在准则，两个重要极限XIDIANUNIVERSITY2n计算极限lim引例+1+2n?+n12n解今Xn2+1n? +2n?+n2211nn≤xnn2+nn?+nn?+nn? +1n2 +1n2 +1n(n+1)n(n+l)适当放、缩1不等式两边极限相等X2(n2 +n)2(n +1)n(n+1)n(n+1)11因为 limli1由夹逼准则，得lim x,2n-0 2(n? + 1)n- 2(n? + n)2

极限存在准则，两个重要极限 不等式两边极限相等 1 lim . → 2 n = n 由夹逼准则,得 x 2 ( 1) lim 2( ) 1 → 2 + = n + n n n n 2 ( 1) lim 2( 1) n n n → n + = + 因为 ， 适当放、缩 引例 2 2 2 1 2 lim . n 1 2 n → n n n n     + + +   + + + 计算极限 令 2 2 2 1 2 1 2 = + + + + + + n n x n n n n 2 2 2 1 2 1 1 1 n n n n  + + + + + + n  x 2 2 2 1 2 n n n n n n n + + + + + + 2 ( 1) 2( ) + +  n n n n 2 ( 1) 2( 1)  + + n n n n x 解

西安毛子科技大学极限存在准则，两个重要极限XIDIAN UNIVERSITY准则I’ 如果函数f(x),g(x)及h(x)满足条件：(1) 当 VxeU(xo,8) 时,g(x)<≤ f(x)≤h(x);(2) lim g(x) =lim h(x)= A,A那么 lim f(x)=A注准则I对于x→等其他情形也成立

极限存在准则，两个重要极限 准则 0 0 lim ( ) lim ( ) , x x x x g x h x A → → （2） = = 注 I 准则 I 对于 x →  等其他情形也成立. 那么 0 lim ( ) x x f x A → = g x f x h x ( ) ( ) ( );   0 （1）当  x U x( , )  时， 如果函数 f x g x ( ), ( ) 及 h x( ) 满足条件：

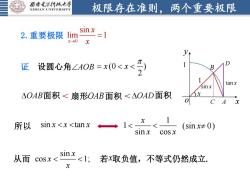
西安毛子科技大学极限存在准则，两个重要极限XIDIANUNIVERSITsinx12.重要极限limx->0xy证设圆心角ZAOB=x(O<x2tanxsinxxAOAB面积<扇形OAB面积<△OAD面积oC+A1x所以sinx<x <tanx(sin x± 0)sin xcos xsinx从而<1: 若x取负值，不等式仍然成立cosxx

极限存在准则，两个重要极限 证 2.重要极限 0 sin lim 1 x x → x = 设圆心角 AOB o C x y OAB 面积  扇形 OAB 面积 OAD 面积 1 1 1 sin tan 2 2 2 所以 x x x   sin cos 1; x x x 从而   1 1 sin cos x x x   (sin 0) x 1 A x 1 (0 ) 2 x x  =    若 x 取负值，不等式仍然成立. sin tan x x x   sin x tan x

西安毛子科技大学极限存在准则，两个重要极限XIDIANUNIVERSITYsinx所以当0x时0x

极限存在准则，两个重要极限 由夹逼准则，即得 sin cos 1 x x x   0 sin lim 1 x x → x = 又 0 limcos 1, x x → = 常用不等式 sin tan x x x   π (0 ) 2  x 所以当 0 | | 时 2 x   

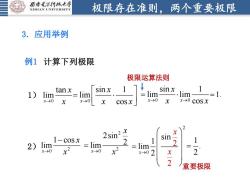
西安毛子科技大学极限存在准则，两个重要极限XIDIANUNIVERSITS3.应用举例例1计算下列极限极限运算法则sinx1一sinxtan x1)limlimlim1lim-x→0x->0x->0x-→>0xxcosxxcos x2sin2xxsin11-cos x212lim= lim2)=limR2x-→0x-→0x→0 2x2重要极限

极限存在准则，两个重要极限 3. 应用举例 例1 计算下列极限 1） =1. 2） 2 0 1 cos lim x x → x − 2 2 0 2sin 2 lim x x → x = 1 . 2 = 2 0 2 2 sin 1 limx 2 x → x     =   0 tan lim x x → x 0 sin 1 lim cos x x → x x   =      0 0 sin 1 lim lim cos x x x → → x x =  重要极限 极限运算法则

西安毛子科技大学极限存在准则，两个重要极限XIDIANUNIVERSITYarcsin x3)limx-→0x解 (换元法）令 t=arcsin x，则x= sint，所以tarcsin xlimlim-1.x→0xt-0 sint

极限存在准则，两个重要极限 3） 0 arcsin lim x x → x 解 令 t x = arcsin , 则 x t = sin , 所以 0 arcsin lim x x → x 0 lim t sin t → t = =1. （换元法）

西安毛子科技大学极限存在准则，两个重要极限XIDIANUNIVERSITY思考题sinxsinx2O=limlimlimsinxX-00X-00x+-00x1sin112Xlim x sinlim xsin lim=1.二=一X>00xxX-00X->00x10lim x sin02x->0x

极限存在准则，两个重要极限 sin lim 1 x x → x = ? 0 1 lim sin 0 x x → x = ? 1 lim sin x x → x = ? × sin lim x x → x = √ 1 lim sin → = x x x sin li 1 1 mx→ x x 1 lim sin x x → x        = 0. 思考题 =1. 