西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第一章 函数与极限 1.3 函数的极限

西安毛子科技大学数学与统计学院XIDIAN UNIVERSITYSchool of mathemnties andstatistics高等数学第三节 函数的极限
第三节 函数的极限

西安毛子科技大学函数的极限XIDIAN UNIVERSITY数列可以看成是函数 x,=f(n),nεNlimx,=a:当n→oo时,x,=f(n)→a.一般函数=f(x),xeD在自变量的某个变化过程中,如果对应的函数值无限接近于某个确定的数,那么这个确定的数就叫做在这一变化过程中函数的极限
函数的极限 数列可以看成是函数 ( ) n x f = n , nN+ lim n n x a → = : ( ) n 当n x f n a → = → 时, . 一般函数 y f = ( ) x ,x D 在自变量的某个变化过程中,如果对应的函数值无限接近 于某个确定的数,那么这个确定的数就叫做在这一变化过程中 函数的极限

西安毛子科技大学函数的极限XIDIANUNIVERSITY一、自变量趋于无穷大时函数的极限定义1设函数f(x)当x小于某数时有定义,若Vε>0,X>0,当x0, X>0&-X定义当x>X时,有If(x)-A<
函数的极限 一、自变量趋于无穷大时函数的极限 lim n 0, n x a → = | | n x a − . 正整数 N , 当 n N 时,有 − N 定义 定义1 时的极限,记作 若 0, X 0, lim ( ) x f x A → + = 则称常数 A 为函数 f x( ) 设函数 大于某数时有定义, 或 f x A x ( ) ( + ) → → 当 + lim ( ) x f x A → + = X 0 x X | ( ) | f x A − . X x X − 小 − − −

西安毛子科技大学函数的极限XIDIAN UNIVERSITY一、自变量趋于无穷大时函数的极限定义2 设函数f(x)当|x|大于某数时有定义,若ε>0,3X>O,当|x[>X时,有Lf(x)-A0,3X>0,8-X定义当1x>X时,有1f(x)-A<6
函数的极限 定义2 时的极限,记作 若 0, X 0, lim ( ) x f x A → = 则称常数 A 为函数 f x( ) 设函数 大于某数时有定义, 或 f x A x ( ) ( ) → → 当 lim ( ) 0, x f x A → = 当 | | x X 时,有 | ( ) | f x A − . − X 定义 X 0, 一、自变量趋于无穷大时函数的极限

西安毛子科技大学函数的极限XIDIANUNIVERSITY例1用定义证明lim二=0x-00X1证>0,要使只要x8rx取X=当|x|>X时,有<8x80f因此 lim=0x-0x
函数的极限 例1 用定义证明 1 lim 0 x→ x = . 证 0, 要使 只要 取 1 X = , 当 时,有 1 0 x − . 因此 o x y 1 y x =
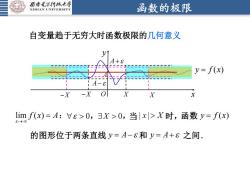
西安毛子科技大孝函数的极限XIDIANUNIVERSITS自变量趋于无穷大时函数极限的几何意义Vy= f(x)A-8xolX-XX-Xlimf(x)=A:Vε>0,X>0,当[x>X时,函数y=f(x)的图形位于两条直线=A-ε和y=A+ε之间
函数的极限 自变量趋于无穷大时函数极限的几何意义 O x y y f x = ( ) A A+ A− −X −X X X lim ( ) x→ f x A = : 0, X 0, 当 时,函数 y f x = ( ) 的图形位于两条直线 y A = − 和 y A = + 之间.

西安毛子科技大学函数的极限XIDIANUNIVERSITY自变量趋于无穷大时函数极限的几何意义VA+Sy= f(x)A-80X-XXx-X定义3 若 lim f(x)= A(lim f(x)= A,lim f(x)= A),则直线y=A是函数=f(x)的图形的水平渐近线
函数的极限 自变量趋于无穷大时函数极限的几何意义 O x y y f x = ( ) A A+ A− −X −X X X 定义3 若 lim ( ) , x f x A → = 则直线 = = y A y f x 是函数 ( )的图形的水平渐近线. ( lim ( ) lim ( ) ) , , x x f x A f x A →+ →− = =
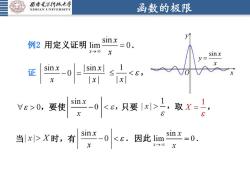
西安毛子科技大学函数的极限XIDIANUNIVERSITSytsinx例2用定义证明lim=0.X-00xsinx1sinxsinx证0V00,RX时,有因此 lim=0.<.xX-00x
函数的极限 例2 用定义证明 sin lim 0 x x → x = . 证 0, 要使 只要 sin | sin | 0 | | x x x x − = 1 | | x , 1 X 取 = , 当 时,有 sin 0 x x − . 因此 sin x y x = O x y

西要毛子科技大学函数的极限XIDIANUNIVERSITS二、自变量趋于有限值时函数的极限×-当x→1时的变化趋势,观察函数 f(x)=x+1和 J;(x)=-Y若当x无限接近于x时,函数Vx-101)x-为函数f(x)当 x→x时的极限
函数的极限 y x = +1 2 1 1 x y x − = − 二、自变量趋于有限值时函数的极限 2 1 2 1 ( ) 1 ) 1 ( 1 x f x x f x x x − → = + = − 观察函数 和 当 时的变化趋势. O x y 1 f x( ) 无限接近于常数 A ,则称常数 A 为函数 f x( ) 当 时的极限. 若当 x 无限接近于 x0 时,函数 y x = +1 2 → ( 1) x → 2 1 2 1 ( 1) x y x x − = → → − | ( ) | f x A − 0 0 | | x x −

西安毛子科技大学函数的极限XIDIAN UNIVERSITY定义4 设函数f(x)在点xo的某一去心邻域内有定义,若>0,3>0,当00, 38>0,8-8定义当0<x-x<S时,有f()-A<8
函数的极限 0, 0, 0 lim ( ) x x f x A → = 定义4 设函数 在点 的某一去心邻域内有定义, 或 若 0, 则称常数 A 为函数 0, f x( ) 当 时的极限. 0 lim ( ) x x f x A → 记作 = 0 f x A x x ( ) ( ) → → 当 − 定义
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第一章 函数与极限 1.2 数列的极限.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第一章 函数与极限 1.1 映射与函数.pptx
- 西安电子科技大学:《高等数学》课程教学大纲 Advanced Mathematics A(I).docx
- 西安电子科技大学:《高等代数》课程PPT教学课件(研讨)第二讲 矩阵计算的应用——复杂网络参数指标.pptx
- 西安电子科技大学:《高等代数》课程教学大纲(研讨)Discussions in Advanced Algebra.docx
- 西安电子科技大学:《高等代数》课程PPT教学课件(研讨)第一讲 行列式的计算方法小结.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)习题课——正交矩阵的性质(讲课:杨忠鹏).ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第九章 欧氏空间 9.7 向量到子空间的距离.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第九章 欧氏空间 9.6 对称矩阵的标准形.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第九章 欧氏空间 9.5 子空间.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第九章 欧氏空间 9.4 正交变换.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第九章 欧氏空间 9.3 同构.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第九章 欧氏空间 9.2 标准正交基.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第九章 欧氏空间 9.1 定义与基本性质.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第八章 λ-矩阵 8.6 若当标准形的理论推导.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第八章 λ-矩阵 8.5 初等因子.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第八章 λ-矩阵 8.4 矩阵的相似.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第八章 λ-矩阵 8.3 不变因子.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第八章 λ-矩阵 8.2 λ─矩阵的标准形.ppt
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第八章 λ-矩阵 8.1 λ─矩阵.ppt
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第一章 函数与极限 1.4 无穷小与无穷大.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第一章 函数与极限 1.5 极限运算法则.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第一章 函数与极限 1.6 极限存在准则、两个重要极限.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第一章 函数与极限 1.7 无穷小的比较.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第一章 函数与极限 1.8 函数的连续性与间断点.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第一章 函数与极限 1.9 连续函数的运算与初等函数的连续性.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第一章 函数与极限 1.10 闭区间上连续函数的性质.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(习题课)第一章 函数与极限(习题选讲).pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(习题课)第一章 函数与极限(习题课).pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第二章 导数与微分 2.1 导数概念.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第二章 导数与微分 2.2 函数的求导法则.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第二章 导数与微分 2.3 高阶导数.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第二章 导数与微分 2.4 隐函数及由参数方程所确定的函数的导数相关变化率.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第二章 导数与微分 2.5 函数的微分.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(习题课)第二章 导数与微分.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第三章 微积分中值定理与导数应用 3.1 微分中值定理.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第三章 微积分中值定理与导数应用 3.2 洛必达法则.pptx
- 西安电子科技大学:《高等数学》课程PPT教学课件(讲稿)第三章 微积分中值定理与导数应用 3.3 泰勒公式.pptx
- 《图论》课程教学资源(书籍文献)Graph Theory(Reinhard Diestel,3rd Edition,Electronic Edition 2005).pdf
- 《图论》课程教学资源(书籍文献)Graph Theory(Reinhard Diestel,5th Edition).pdf
