西安电子科技大学：《高等数学》课程PPT教学课件（讲稿）第二章 导数与微分 2.4 隐函数及由参数方程所确定的函数的导数相关变化率

西安毛子科技大学数学与统计学院School ofmathematies and statisticsXIDIAN UNIVERSITY西等数学第四节隐函数及由参数方程所确定的函数的导数相关变化率

第四节 隐函数及由参数方程 所确定的函数的导数 相关变化率

西安毛子科技大学隐函数的导数IDIAN UNIVERSITY一、隐函数的导数若由方程 F(x,y)=O 可确定 关于x 的函数 =f(x)则称 y= f(x)为由方程 F(x,y)=O 所确定的隐函数.由=f(x）表示的函数称为显函数把一个隐函数化成显函数，叫做隐函数的显化例如，x-3-1=0可确定显函数=x-1ys+2y-x-3x=0可确定是x的函数但此隐函数不能显化

隐函数的导数 一、隐函数的导数 例如, 但此隐函数不能显化. 若由方程 可确定 y 关于 x 的函数 y f x = ( ), F x y ( , ) 0 = 则称 y f x = ( ) 为由方程 F x y ( , ) 0 = 所确定的隐函数. 由 y f x = ( ) 表示的函数称为显函数. . x y − − = 3 1 0 可确定显函数 3 y x = −1. 可确定 是 的函数, 5 7 y y x x + − − = 2 3 0 y x 把一个隐函数化成显函数 叫做隐函数的显化

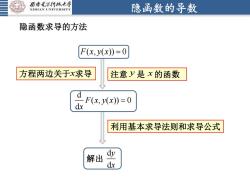
西安毛子科技大学隐函数的导数XIDIAN UNIVERSITY隐函数求导的方法F(x, y(x)=0方程两边关于x求导注意是x的函数F(x, (x)=0dx利用基本求导法则和求导公式dy解出dx

隐函数的导数 隐函数求导的方法 方程两边关于 x 求导 利用基本求导法则和求导公式 注意 y 是 x 的函数 F x y x ( , ( )) 0 = d ( , ( )) 0 d F x y x x = 解出 d d y x

西要毛子科技大学隐函数的导数XIDIANUNIVERSITY例1求由方程ys+2-x-3x=0所确定的隐函数=f(x)在x=0处的导数y'lx=0解原方程两边分别对x求导得(y)+(2y)-(x)-(3x)=(0)' 5y4y' +2y-1 -21x = 01+21x6由此得5y4+21+21x61当x=0 时，从原方程得y=O，所以yl-25y4 +2

隐函数的导数 解 4 5y 由此得 例1 求由方程 所确定的隐函数 在 5 7 y y x x + − − = 2 3 0 y f x = ( ) x = 0 处的导数 0 | . x y =  原方程两边分别对 x 求导得 6 4 1 21 . 5 2 x y y +  = + 当 x = 0 时, 从原方程得 y = 0, y  +2y −1 0. 6 − = 21x 5 7 ( ) (2 ) ( ) (3 ) (0) y y x x      + − − = 6 0 0 4 1 21 1 | | . 5 2 2 x x x y y = = +  = = + 所以

西安毛子科技大学隐函数的导数XIDIAN UNIVERSITY例2设函数=(x)由方程e+xy=e所确定，求"(O)解1应用隐函数求导法则，得ye'.y' + y+x.y' =0一e'+x'的表达式两边再对x求导，得"=- '(e'+x)-y(e"-y'+1)(e' +x)V当x=0时，由e'+xy=ey=l, (0)=e' +x|x=0e(0)=[-'(e'+x)-(cy'+1)]于是e?(e' +x)?

隐函数的导数 例2 设函数 y y x = ( ) 由方程 e e y + = xy 所确定，求 y (0). 解1 应用隐函数求导法则，得 e y  y  . e y y y x  = − + 2 (e ) y + x 当 x = 0 时，由 y =1， 2 2 0 (e ) (e 1) 1 (0) . (e ) e y y y x y x y y y x =      + −   +  = − =     + y  的表达式两边再对 x 求导，得 e e y + = xy 0 1 (0) e e y x y y x = −  = = − + ， y  (e ) y + x y (e 1) y  + y  + y x y +   = 0 于是 y  = − −

西安毛子科技大学隐函数的导数IDIANUNIVERSITY例2设函数=(x)由方程e+xy=e所确定，求"()解2应用隐函数求导法则，得①e'.y'+ y+x.y'=0①式两端同时对x再求导，得②e'.y'.y'+e'.y" +y' +y'+x.y"=01由e'+xy=e知x=0 时=l，代入①得y(O)=e1"代入②式得 "(0)=将 x=0,=1, (0)=-=e?-

隐函数的导数 例2 设函数 y y x = ( ) 由方程 e e y + = xy 所确定，求 y (0). 解2 应用隐函数求导法则，得 e y  y  y x y +   = 0 ① ①式两端同时对 x 再求导，得 + y  + e e = 0 y y   +  y y y    + y x y   +  由 e e 知 x = 0 时 y =1, y + = xy 1 (0) e 代入 ① 得 y  = − . ② 2 1 (0) . e 将 x = 0 ， y =1 ， 代入 式得 y  = 1 (0) e y  = − ②

西安毛子科技大学隐函数的导数XIDIAN UNIVERSITYy?3 3)处的切线方程。1 在(2,例3 求椭圆216911V=0解把椭圆方程的两边同时对x求导，得2x+2y9169x从而D16y3在(2.号V3)点处，所求切线的斜率为k= l4 2V3D=(x-2),所求的切线方程为J24即/3x+4y-8/3=0

隐函数的导数 例3 求椭圆 在 处的切线方程. 2 2 1 16 9 x y + = 3 (2, 3) 2 解 1 1 2 2 0, 16 9 x y y +  = 从而 9 . 16 x y y  = − 所求的切线方程为 2 3 | . 4 x k y = = = −  把椭圆方程的两边同时对 x 求导, 得 在 点处，所求切线的斜率为 3 (2, 3) 2 3 3 3 ( 2), 2 4 y x − = − − 即 3 4 8 3 0. x y + − =

西安毛子科技大学隐函数的导数KIDIANUNIVERSITY例4 已知 f(x)具有二阶导数，且 f'(O)=f"(O)=1，函数=(x)由方程 -xe-l=O所确定,设z=f(ln-sinx),d?zdz求dxdx?-0dz解f'(ln y-sin x)(-y'-cos x)dx1d?z=[f"(In y- sin x)(_'-cos x)](二 y - cos x)dx+f'(ln y- sin x) {y-(y)+ sin x]= f"(ln y-sin x) (_y'-cos x)* + f"(ln y-sin x) ("y-(g)+sin x)y

隐函数的导数 例4 已知 f x( ) 具有二阶导数，且 f f   (0) (0) 1, = = 函数 y y x = ( ) 由方程 1 0 所确定,设 y y xe − − = z f y x = − (ln sin ), 求 2 2 0 0 d d , d d x x z z x x = = 解 d (ln sin ) d z f y x x = −  1 ( cos ) y x y  − 2 2 d 1 [ (ln sin ) ( cos )] d z f y x y x x y = −  −   1 ( cos ) y x y  − + − f y x (ln sin ) 2 2 ( ) [ sin ] y y y x y   −  + 2 2 2 1 ( ) (ln sin ) ( cos ) (ln sin ) ( sin ) y y y f y x y x f y x x y y   − = −  − + −  +   

西安毛子科技大学隐函数的导数XIDIAN UNIVERSITS例4 已知 f(x)具有二阶导数，且 f(O)=f"(O)=1，函数=(x)由方程 -xe-l=O所确定,设z=f(ln-sinx),d’zdz求dx|x=0dx?下面求 y,"-xe-1=O两边关于x求导ey'-(e'+xe'y')=0 → y'-1- xe.. y"-e'y'l-xe')+e'(e'+xe'y)(1- xe')dzx=0 =y=l, y'=e, y"=2e?=e-1二dx x=0dz同理可得dx?

隐函数的导数 下面求 y y   , . 1 0 y y xe − − = 两边关于 x 求导 ( ) 0 y y y e xe y   − + = 1 y y e y xe  = − 2 (1 ) ( ) (1 ) y y y y y y e y xe e e xe y y xe   − + +  = − x = 0 2  = = = y y e y e 1, , 2   0 d 1 d x z e x =  = − 同理可得 2 2 0 d d x z x = 例4 已知 f x( ) 具有二阶导数，且 f f   (0) (0) 1, = = 函数 y y x = ( ) 由方程 1 0 所确定,设 y y xe − − = z f y x = − (ln sin ), 求 2 2 0 0 d d , d d x x z z x x = =

西安毛子科技大学隐函数的导数XIDIANUNIVERSITY对数求导法dyy= f(x)In /[y/= ln / f(x)|两边求导再求解dx不论=f(x)0f'(x)(lnf(x)'= f(x)

隐函数的导数 对数求导法 不论 y f x =  ( ) 0, 还是 y f x =  ( ) 0. ( ) (ln| ( )|) = ( ) f x f x f x   y f x = ( ) ln | | ln | ( ) | y f x = 两边求导再求解 d d y x