西安电子科技大学：《概率论与数理统计》课程教学资源（PPT课件讲稿）数值实验——第一部分 古典概型

内容介绍 一、古典概型 MATLAB常用的及与随机数产生相关的函数 实验1：计算超几何分布 实验2：频率稳定性实验 实验3：利用频率估计自然对数底e 实验4：蒲丰投针实验，利用频率估计圆周率π 实验5：生日悖论实验 2/21

内容介绍 一、古典概型 MATLAB常用的及与随机数产生相关的函数 实验1：计算超几何分布 实验2：频率稳定性实验 实验3：利用频率估计自然对数底e 实验4：蒲丰投针实验，利用频率估计圆周率 实验5：生日悖论实验 2/21

一、古典概型 利用ATLAB软件的图形可视功能将概率统计的内容用图形表示出来， 以加深对概率的理解 )MATLAB常用的及与随机数产生相关的函数 factorial(n)：阶乘，nl,可通过阶乘来计算排列组合数 1.rand(m,n):生成m×n的随机矩阵，每个元素都在(0,1)间，生成方式为 均匀分布。 ● 2.randn(m,n):生成m×n的随机矩阵，每个元素都在(0,1)间，生成方式为 正态分布 。3.randperm(m):生成一个1m的随机整数排列 。4.perms(1:n):生成一个1~n的全排列，共nl个 5.取整函数系列： (1)fix☒)：截尾法取整； (2)floor(x):退一法取整（不超过x的最大整数）；向负方向舍入 (3)ceil(x):进一法取整(=floor(x)+1); 向正方向舍入 (4)round(x):四舍五入法取整。 。6.unique(a):合并a中相同的项 ●7.prod(x):向量x的所有分量元素的积 3/21

一、古典概型  利用MATLAB 软件的图形可视功能将概率统计的内容用图形表示出来， 以加深对概率的理解  MATLAB常用的及与随机数产生相关的函数 ⚫ factorial(n) ：阶乘，n!，可通过阶乘来计算排列组合数 ⚫ 1.rand(m,n)：生成m×n的随机矩阵，每个元素都在(0,1)间，生成方式为 均匀分布。 ⚫ 2.randn(m,n)：生成m×n的随机矩阵，每个元素都在(0,1)间，生成方式为 正态分布 ⚫ 3.randperm(m)：生成一个1~m的随机整数排列 ⚫ 4.perms(1:n)：生成一个1~n的全排列，共n!个 ⚫ 5.取整函数系列： （1）fix(x)：截尾法取整； （2）floor(x)：退一法取整（不超过x的最大整数）；向负方向舍入 （3）ceil(x)：进一法取整（= floor(x)+1）； 向正方向舍入 （4）round(x)：四舍五入法取整。 ⚫ 6.unique(a)：合并a中相同的项 ⚫ 7.prod(x)：向量x的所有分量元素的积 3/21

一、古典概型 示例： >>rand(1)%生成一个(0,1)间的随机数 ans=0.8147 >>rand(2,2)%生成一个2×2阶(0,1)间的随机数矩阵 ans=0.9134 0.0975 0.63240.2785 >>randperm(5)%生成一个1~5的随机整数排列 ans=41523 >>a=[1242332]; unique(a) ans=1234 4/21

一、古典概型  示例： >> rand(1) %生成一个(0,1)间的随机数 ans = 0.8147 >> rand(2,2) %生成一个2×2阶(0,1)间的随机数矩阵 ans = 0.9134 0.0975 0.6324 0.2785 >> randperm(5) %生成一个1~5的随机整数排列 ans = 4 1 5 2 3 >> a=[1 2 4 2 3 3 2]; unique(a) ans = 1 2 3 4 4/21

实验1：计算超几何分布的结果 设有N件产品，其中D件次品，今从中任取件 ●问其中恰有k(≤D)件次品的概率是多少？ CXCD （令N=10,D=3,=4,=2) 解：编辑组合函数zuhe.m文件 function y=Com(n,r) y=factorial(n)/(factorial(r)*factorial(n-r)) 计算如下： 。>>N=10;D=3;n=4;k=2; 0p=Com(3,2)*Com(10-3,4-2)/Com(10,4)=0.3 5/21

 实验 1：计算超几何分布的结果 ⚫ 设有N件产品，其中D件次品，今从中任取n件 ⚫ 问其中恰有k(kD)件次品的概率是多少？ ⚫ （令N=10，D=3，n=4，k=2）  解：编辑组合函数zuhe.m文件 ⚫ function y=Com(n,r) ⚫ y=factorial(n)/(factorial(r)*factorial(n-r))  计算如下： ⚫ >> N=10; D=3; n=4; k=2; ⚫ p=Com(3,2)*Com(10-3,4-2)/Com(10,4)=0.3 n k N n k D N D C C C −  − 5/21

。实验2频率稳定性实验 ·随机投掷均匀硬币，观察国徽朝上与国徽朝下的频率 解 >>n=3000-100000000;m=0; for i=1:n t=randperm(2);%生成一个1~2的随机整数排列 x=t-1;%生成一个0~1的随机整数排列 y=x(1);%取x排列的第一个值 if y==0; m=m+1; end end p1=m/n p2=1-p1 6/21

 实验2 频率稳定性实验 ⚫ 随机投掷均匀硬币，观察国徽朝上与国徽朝下的频率  解 ⚫ >> n= 3000~100000000;m=0; ⚫ for i=1:n ⚫ t=randperm(2); %生成一个1~2的随机整数排列 ⚫ x=t-1; %生成一个0~1的随机整数排列 ⚫ y=x(1); %取x排列的第一个值 ⚫ if y==0; ⚫ m=m+1; ⚫ end ⚫ end ⚫ p1=m/n ⚫ p2=1-p1 6/21

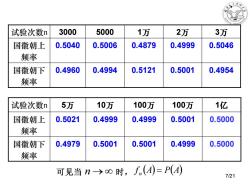
试验次数n 3000 5000 1万 2万 3万 国徽朝上 0.5040 0.5006 0.4879 0.4999 0.5046 频率 国徽朝下 0.4960 0.4994 0.5121 0.5001 0.4954 频率 试验次数n 5万 10万 100万 100万 1亿 国徽朝上 0.5021 0.4999 0.4999 0.5001 0.5000 频率 国徽朝下 0.4979 0.5001 0.5001 0.4999 0.5000 频率 可见当n→o时，fn(A)=P(A 7/21

试验次数n 3000 5000 1万 2万 3万 国徽朝上 频率 0.5040 0.5006 0.4879 0.4999 0.5046 国徽朝下 频率 0.4960 0.4994 0.5121 0.5001 0.4954 试验次数n 5万 10万 100万 100万 1亿 国徽朝上 频率 0.5021 0.4999 0.4999 0.5001 0.5000 国徽朝下 频率 0.4979 0.5001 0.5001 0.4999 0.5000 f (A) P(A) 可见当 n → 时， n = 7/21

。实验3用频率估计自然对数e 。某班有个人，每人各有一支枪，这些枪外形一样。某次夜间紧急 集合，若每人随机地取走一支枪，求没有一个人拿到自己枪的概率？ 解：记事件4为第个人拿到自已枪，事件A,为第个人没拿到自己枪， 易知： 。p4)=;Pa)=",=12,n n 0】 又记p为没有一个人拿到自己枪的概率。 以a瓦)=1-P04 由乘法公式可知 PlA）上P氏4PA)0s1<js )-4)r4)2ik) P444)广 8/21

 实验3 用频率估计自然对数e ⚫ 某班有n个人，每人各有一支枪，这些枪外形一样。某次夜间紧急 集合，若每人随机地取走一支枪，求没有一个人拿到自己枪的概率？  解：记事件Ai为第i个人拿到自已枪，事件 为第i个人没拿到自己枪， 易知： ⚫ ； ， ⚫ 又记 p0为没有一个人拿到自己枪的概率。 ⚫ 由乘法公式可知 ⚫ … … Ai ( ) n P Ai 1 = ( ) n n P Ai −1 = (i =1,2,,n)         = = − =   n i p P A A A P Ai 1 0 ( 1 2 n ) 1 ( ) ! 1 1 2 3 n P A A A An = ( ) ( ) ( ) ( ) ( i j n) n n P Ai Aj P Ai P Aj Ai    − =  = 1 1 1 ( ) ( ) ( ) ( )( ) ( i j k n) n n n P Ai Aj Ak P Ai Aj P A Aj A     − − =  = 1 1 2 1 k i 8/21

于是 定P)-L立PA上G u4A小Fh物习 C l≤i<i<k≤n u44日 所以 0p-o+g] 特别地，当n较大时，po≈e。 因此，可随机模拟出没有人拿到自己枪的频率，根据频率的 稳定性，近似当做概率，然后去估计自然对数。并考虑估计精 度与人数是否有关系，为什么。算法如下： 9/21

于是 所以 特别地，当n较大时， 。 因此，可随机模拟出没有人拿到自己枪的频率，根据频率的 稳定性，近似当做概率，然后去估计自然对数e。并考虑估计精 度与人数是否有关系，为什么。算法如下： ( ) ( ) ( ) ( ) ( )( ) ( ) ! 1 , 1 2 1 1, 1 2 3 3 1 2 1 1 n P A A A A n n n C P A A A n n C P A P A A n n n i j k n i j k n n i j n i j n i i = − − = − = =        =      ( ) ( )( ) ( ) ( ) = + = −  =      − + + − − + − = − −         = − n k n k n n n i i n n n n k C n n C p P A 0 2 3 1 1 0 ! 1 ! 1 1 1 2 1  1 1  1 0 − p  e 9/21

1、产生n个随机数的随机序列； ·2、检验随机列与自然列是否至少有一个配对； 3、对没有一个配对的序列进行累积t; 。4、重复1、2、3步m次； m 5计e= ⊙具体程序及相关结果如下页图 。注：自然常数≥2.7183

 1、产生n个随机数的随机序列；  2、检验随机列与自然列是否至少有一个配对；  3、对没有一个配对的序列进行累积 t；  4、重复1、2、3步 m 次；  5、估计  具体程序及相关结果如下页图 ⚫ 注：自然常数 e≈2.7183 t m e =

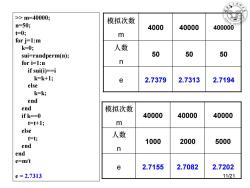
>>m=40000; 模拟次数 n=50; 4000 40000 400000 t=0; m for j=1:m k=0; 人数 sui=randperm(n); 50 50 50 for i=1:n n if sui(i)==i k=k+1; e 2.7379 2.7313 2.7194 else k=k; end end 模拟次数 if k==0 40000 40000 40000 t=t+1; m else t=t; 人数 1000 2000 5000 end n end e=m/t e 2.7155 2.7082 2.7202 e=2.7313 11121

>> m=40000; n=50; t=0; for j=1:m k=0; sui=randperm(n); for i=1:n if sui(i)==i k=k+1; else k=k; end end if k==0 t=t+1; elset= t ; end end e=m/ t e = 2.7313 模拟次数 m 40000 40000 40000 人数n 1000 2000 5000 e 2.7155 2.7082 2.7202 模拟次数 m 4000 40000 400000 人数n 50 50 50 e 2.7379 2.7313 2.7194 11/21