南京大学：《计算机问题求解》课程教学资源（课件讲稿）Hashing方法

计算机问题求解一论题2-13 ashing方法 2014年06月10日

计算机问题求解 – 论题2-13 - Hashing方法 2014年06月10日

Hashing 0 U (universe of keys) h(k1) k h(k K ka (actual h依)=k) keys) h(ka) m-1 间题1： 所谓“Hashing”方法是 用来解决什么间题的？

Hashing

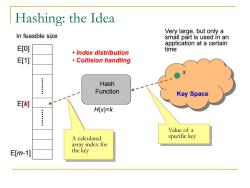
Hashing:the Idea Very large,but only a In feasible size small part is used in an application at a certain E[0] ·Index distribution time 耳1] Collision handling : Hash Function Key Space E[k] H(x)=k Value of a A calculated specific key array index for E[m-1] the key

Hashing: the Idea Key Space Hash Function E[0] E[1] E[m-1] Value of a specific key A calculated array index for the key Very large, but only a small part is used in an application at a certain time In feasible size • Index distribution • Collision handling E[k] x H(x)=k

间题2： Co1 ision是什么意思？ 它是如何产生的？

间题3： 假设分配的存储区为k个单元， 插入个键值。对于某个特定位 置，落到该位置的对象的期望值 是多少？为什么？ 顺便问一下，只插入2个键值， 发生碰撞的概率是多大？

顺便问一下，只插入2个键值， 发生碰撞的概率是多大？

模型：将插入n个对象看作n个独立试验的 序列。每个试验的结果是{1,2，…，} 中的一个值。 假设：每个实验的结果是任意一个允许值 的概率是一样的。 (uniformly distributed) In hashing n items into a hash table of size k the expected number of items that hash to any one location is /k. :loading factor(负载因子)

模型: 将插入n个对象看作n个独立试验的 序列。每个试验的结果是{1,2,…,k} 中的一个值。 假设：每个实验的结果是任意一个允许值 的概率是一样的。 (uniformly distributed) : loading factor(负载因子)

现在考虑特定单元为空的概率 同样的independent trials process,可以根据 需要指定不同的outcomes: 口k个不同的outcomes:单元1,2，.，k 口2个outcomes:单元i,非单元i 问题4： 问题4： 插入n个对象后，单 插入n个对象后，空单 元仍然是空的，概 元的期望是多少？为 率是多少？ 什么？ -(1-1/k)

现在考虑特定单元为空的概率  同样的independent trials process，可以根据 需要指定不同的outcomes:  k个不同的outcomes: 单元1,2,…,k  2个outcomes: 单元i, 非单元i

一个概率悖论 假设有n个存储单元，在插入n个对象后 ·第ⅰ个单元已放入对象数期望值是： 2 =1 换句话说，没有空的单元(？) n ·整个存储区内空单元的期望数是： 1--036m e 问题5； 你能解释这个悖论”吗？

一个概率悖论 假设有n个存储单元，在插入n个对象后 • 第i个单元已放入对象数期望值是： • 整个存储区内空单元的期望数是：  1 n n n e n n n n 0.368 1 1          换句话说，没有空的单元（？）

冲突：可能性有多大？ 在k个单元的存储区内插入个对象： E(collisions)=n-E(occupied locations) =n-+E(empty locations) In hashing n items into a hash table with k locations,the expected number of collisions is n-k+k(1-1/k)". 找一点感觉： 假如在100个单元的存储区内插入100个对象， 发生的碰撞数的期望值就是大约37次

冲突: 可能性有多大？ 在k个单元的存储区内插入n个对象： 找一点感觉： 假如在100个单元的存储区内插入100个对象， 发生的碰撞数的期望值就是大约37次

没有空单元：需要插入多少对象？ 先考虑一个“子问题”：使得被占单元数从达到-1增加到达 到i,需要插入多少对象（期望）？ E(X1)=1,E(X2)=k/(k-1),. In general,we have that Xi counts the number of trials until success in an independent trials process with probability of success(k-i+1)/k,and thus, the expected number of steps until the first success is k/(k-i+1),which is the expected value of Xi. E(X)= w名斤宫-=点空 Θ(k logk) 给你一点感觉： k=10000,这个值大约是98000

没有空单元：需要插入多少对象？ 先考虑一个“子问题”：使得被占单元数从达到 i-1 增加到达 到 i, 需要插入多少对象（期望）？ , , …… 给你一点感觉： 当k=10000, 这个值大约是98000