南京大学:《计算机问题求解》课程教学资源(课件讲稿)函数

计算机问题求解一论题1-10 函数 2015年12月3日
计算机问题求解 – 论题1-10 - 函数 2015年12月3日

间题1: “函数》与“关系》有什么异同? 函数”与“集合”是什么关系? 令关系f:R→R,fX)=+1,f是否是函数? 就上述关系,我们熟悉的f(2)该如何表示? f(2)={3}?f2)=3?
令关系:RR, (x) = x+1, 是否是函数? 就上述关系,我们熟悉的(2)该如何表示? (2)={3}?(2)=3?

函数的型构(signature): f:R→R,f(X)=X+1 问题2:你能用上例来解释什么是函数的domain? Codomain?Range? 你能用上例来解释什么是well defined function? 你能否构造一个不是well defined function?
函数的型构(signature): :RR, (x) = x+1 问题2:你能用上例来解释什么是函数的domain? Codomain?Range? 你能用上例来解释什么是well defined function? 你能否构造一个不是well defined function?

4 You probably learned that a function f R->R can be repre- sented by a graph,and that there is a vertical line test to determine whether or not f is a function (See Figure above) Which condition in the definition corresponds to the vertical line test?Why? 问题3: 你是否能解释一下?
( See Figure above)

When you define a new mathematical concept,it's always a good idea to think about it and pose questions.Of course,it's also a good idea to answer those questions,if you can.We now turn to some questions that we find interesting.See if you can think of some questions on your own. 问题4: 书中提出了什么问题?你想 出了什么“自己”的问题吗?

问题5: 函数相等到底是什么含义? 函数作为关系,会让你想起什么? 函数作为集合,会让你想起什么? 函数作为”函数“,它们的相等,会让你 想起什么?
函数相等到底是什么含义? 函数作为关系,会让你想起什么? 函数作为集合,会让你想起什么? 函数作为”函数“,它们的相等,会让你 想起什么? 问题5:

几种特殊的函数 a满射onto of:A→B是满射的:ranf=B,if.yeB,xeA,使得f(X)=y ■单射(one to one) of:A→B是单射的:ye ranf,x∈A,使得f()=yif. X1,x2∈A,若x1≠x2'则f(X1)≠f(X2)if.x1,X2∈A,若f(X1) =fX2j,则x=x2 ■双射(一一对应的) 口满射+单射
几种特殊的函数 满射onto :AB是满射的:ran=B, iff. yB, xA, 使得(x)=y 单射(one to one) :AB是单射的:y ran, !xA, 使得(x)=y iff. x1 ,x2A, 若x1 x2,则(x1 ) (x2 ) iff. x1 ,x2A, 若(x1 ) =(x2 ),则x1 =x2。 双射(一一对应的) 满射+单射

几种特殊的函数:例子 ■f:R-→R,fX)=-x2+2X-1 ■f:Z+→R,f(x)=lnx,单射 问题6:为什么? ■f:R→Z,fx)=Lx,满射 ·f:R→R,fX)=2x-1,双射 ■f:R+→R+,fX)=(x2+1)/X 口注意:x)≥2,而对任意正实数x,fx)=1/x) ·f:RxR→RxR,f()=,双射。 ■f:NxN→N,f()=|x2-y2I
几种特殊的函数:例子 :RR, (x)= -x 2+2x-1 :Z+R, (x)= ln x, 单射 :RZ, (x)= x, 满射 :RR, (x)= 2x-1,双射 :R+R+ , (x)= (x2+1)/x 注意:f(x)2, 而对任意正实数x,f(x)=f(1/x) :RRRR, () = , 双射。 :NNN, () = | x 2 -y 2 |

有限集合上一一对应的函数的例子 ■S={1,2,3},可以在S上定义6个不同的一一对应 的函数(侮一个称为一个“置换”):
有限集合上一一对应的函数的例子 S={1,2,3}, 可以在S上定义6个不同的一一对应 的函数 (每一个称为一个“置换”): 1 2 3 1 2 3 e 2 3 1 1 2 3 3 1 2 1 2 3 1 3 2 1 2 3 3 2 1 1 2 3 2 1 3 1 2 3
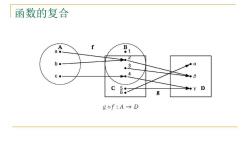
函数的复合 A f B a● 1 b● 3 C● B C 56 g gof:A→D
函数的复合
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)关系及其基本性质.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)什么样的推理是正确的.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)为什么计算机能解题.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)不同的程序设计方法.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)Hashing方法.pdf
- Go To Statement Considered Harmful.pdf
- What is System Hang and How to Handle it?.pdf
- How Far We Have Progressed in the Journey? An Examination of Cross-Project Defect Prediction.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)关于问题求解的几个思考.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)随机算法的概念.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)群与拉格郎日定理.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)线性规划.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)矩阵计算.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)平面图与图着色.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)Dijkstra算法正确性.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)图的计算机表示以及遍历.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)动态规划.pdf
- 高等教育出版社:《数据库系统实用教程》教材PDF电子版(2006,勘误表).pdf
- 高等教育出版社:《数据库系统实用教程》教材PDF电子版(2006,徐洁磐、柏文阳、刘奇志).pdf
- 南京大学:《数据库概论 Introduction to Databases》课程教学资源(教学大纲,胡伟).pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)分治法与递归.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)基本数据结构.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)堆与堆排序.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)如何将算法告诉计算机.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)布尔代数.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)常用的证明方法及其逻辑正确性.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)排序与选择.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)数据与数据结构.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)有限与无限.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)树及搜索树.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)概率分析与随机算法.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)离散概率基础.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)算法方法.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)算法正确性.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)算法的基本结构.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)算法的效率.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)组合与计数.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)计算思维引导.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)递归及其数学基础.pdf
- 南京大学:《计算机问题求解》课程教学资源(课件讲稿)集合及其运算.pdf
