南京大学：《计算机问题求解》课程教学资源（课件讲稿）矩阵计算

计算机问题求解-论题3-14 。矩阵计算 2014年12月15日

计算机问题求解 – 论题3-14 - 矩阵计算 2014 年12 月15 日

自学问题： 什么是forward substitution?

矩阵的逆与线性方程组的解 a1x1+a12x2+…+a1mxn=b1】 azx+axx2+..+azn b2 ( an1x1十an2X2+…十AnnXn= bn】 d11 d12 d21 d22 d2n b2 : g anl dn2 ann Xn or,equivalently,letting A=(ai),x =(xi),and b =(bi),as Ax =b. If A is nonsingular,it possesses an inverse A-,and x=A-b

矩阵的逆与线性方程组的解

逆矩阵存在的条件 A square matrix has full rank if and only if it is nonsingular. A matrix A has full column rank if and only if it does not have a null vector. A square matrix A is singular if and only if it has a null vector. An nx n matrix A is singular if and only if det(A)=0 这是什么意思？

逆矩阵存在的条件 这是什么意思？

问题2： 如何计算非奇异矩阵的逆？ 1:矩阵A的逆=A的伴随矩阵/行列式A的值 2:矩阵A的逆：对(AE)进行行初等变换得到(EA1)

1：矩阵A的逆=A的伴随矩阵/行列式A的值 2：矩阵A的逆：对(A|E)进行行初等变换得到(E|A-1)

2 2 1 例：求3阶方阵A= 31 5 的逆矩阵。 23 3 解：|A|=1,M=-7,M2=-6,M3=3, M21=4,M2=3,M3=-2, M31=9,M32=7,M3=-4, 则 A A A31 An As Aus A23 A33 M -M M -7 -4 -MR Mn -M2 三 3 -7 M3 -M2 M3 3 2 -4

(1 23 例1 A=221,求A1. 设 3 43 12 310 0 解(AE)= 221 0 10 343 0 0 1 22 2 3 0 -2 5-210 +2 3-3新0-2 -6-301g-2

问题3： 为什么通常不直接用求 逆矩阵的办法来解线性 方程组？

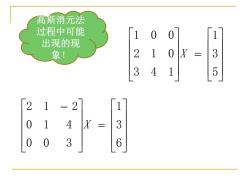
高斯消元法 过程中可能 1 0 0 出现的现 象！ 2 1 0 X 三 3 3 4 [5 2 1 2 1 0 1 4 X 三 3 0 3 16

                     5 3 1 143 012 001 X                       6 3 1 300 410 212 X 高斯消元法 过程中可能 出现的现 象！

问题4： 三角阵会给解线性方程 组带来什么便利？