同济大学：《传播信道特征估计和建模》课程教案讲义（射线追踪）02 Geometrical Theory of Propagation I - The ray concept – Reflection and transmission

Deterministic radio propagation modeling and ray tracing 1 Introduction to deterministic propagation modelling 2) Geometrical Theory of Propagation I-The ray concept-Reflection and transmission 3) Geometrical Theory of Propagation II-Diffraction,multipath 4) Ray Tracing I 5) Ray Tracing II-Diffuse scattering modelling 6) Deterministic channel modelling I 7) Deterministic channel modelling II-Examples 8) Project -discussion

1 Deterministic radio propagation modeling and ray tracing 1) Introduction to deterministic propagation modelling 2) Geometrical Theory of Propagation I - The ray concept – Reflection and transmission 3) Geometrical Theory of Propagation II - Diffraction, multipath 4) Ray Tracing I 5) Ray Tracing II – Diffuse scattering modelling 6) Deterministic channel modelling I 7) Deterministic channel modelling II – Examples 8) Project - discussion

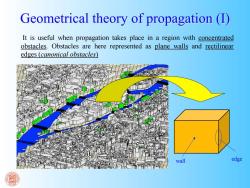
Geometrical theory of propagation(D) It is useful when propagation takes place in a region with concentrated obstacles.Obstacles are here represented as plane walls and rectilinear edges (canonical obstacles) wall edge

Geometrical theory of propagation (I) It is useful when propagation takes place in a region with concentrated obstacles. Obstacles are here represented as plane walls and rectilinear edges (canonical obstacles) wall edge

Geometrical theory of propagation(ID) electromagnetic constants: air wall(generic medium) 1 e,36m 10 Farad/m electric permittivity 4。=4π10Heny/m l=。 magnetic permeability 0=0 o (if lossy) electric conductivity e.=e+ 三 complex permittivity j0 n=1 n 。 refraction index 1。=120π2 intrinsic impedance

Geometrical theory of propagation (II) electromagnetic constants: air wall (generic medium) ε o = 1 36π 10−9 Farad / m ε electric permittivity µo = 4π 10−7 Henry / m µ = µo magnetic permeability σ = 0 σ (if lossy) electric conductivity ε c = ε + σ jω = ε − j σ ω complex permittivity n=1 n  ε c ε o refraction index ηo = 120π Ω η  µ ε c = µo ε c intrinsic impedance

Geometrical theory of propagation (ID) Geometrical theory of propagation is an extension of Geometrical Optics, (GO)but is not limited to optical frequencies Like GO,it corresponds to an asymptotic,high-frequency approximation of basic electromagnetic theory,and is based on the concept of ray Since GO does not account for diffraction,then diffraction is introduced through an extension called Geometrical Theory of Diffraction(GTD) The combination of GO and GTD,applied to radio wave propagation may be called Geometrical Theory of Propagation(GTP) GTP is the base of deterministic,ray-based propagation models(ray-tracing etc.)

Geometrical theory of propagation (II) • Geometrical theory of propagation is an extension of Geometrical Optics, (GO) but is not limited to optical frequencies • Like GO, it corresponds to an asymptotic, high-frequency approximation of basic electromagnetic theory, and is based on the concept of ray • Since GO does not account for diffraction, then diffraction is introduced through an extension called Geometrical Theory of Diffraction (GTD) • The combination of GO and GTD, applied to radio wave propagation may be called Geometrical Theory of Propagation (GTP) • GTP is the base of deterministic, ray-based propagation models (ray-tracing etc.)

Tx antenna in free space Far field:(r>>r>>D,antenna's dimension) (Spherical wave) r.0.p)=E(0p7 vectorial amplitude propagation B= 2元 E。⊥T factor E Complex vector or phasor,so that e(r.0.p.t)-RefE(r.0.p)e]

Tx antenna in free space ? Far field: ( r >> λ r >> D , antenna’s dimension) Tx (Spherical wave)  E(r,θ,ϕ) ≈  Eo (θ,ϕ) e− jβr r vectorial amplitude  e (r,θ,ϕ,t) = ℜe  E(r,θ,ϕ)ejωt { }  E Complex vector or phasor, so that propagation factor β = 2π E λ o ⊥ r r

Far field expressions (r>λr>D)》 头 ao-员[xapk町 E(6,p) .dp)-ix x 2 2n Poynting vector Antenna's radiation vector source (antenna) P' Mme.p)=j.Pep[i小aW 上 j,≠0

 E(r,θ,ϕ) ≈ − j η 2λ ˆ i r ×  M (θ,ϕ) × ˆ i r ⎡ ⎣ ⎤ ⎦ e− jβr r  H (r,θ,ϕ) ≈ 1 η ˆ i r ×  E  S= 1 2  E ×  H* =  E 2 2η ˆ i r  M(θ,ϕ) ≈  Ji(P') V ' ∫ exp jβ  r '⋅ˆ i ( r ) ⎡ ⎣ ⎤ ⎦dV ' Far field expressions ( r >> λ r >> D ) Antenna’ s radiation vector V’ P’ P r ’ r y x z D  Eo (θ,ϕ)   Ji ≠  0                               M t  source (antenna) Poynting vector

Polarization vector p The polarization vector defines the polarization of the field (and also of the antenna) It is strictly related to the radiation vector M 二J2沟 =e明.e以= 一=M 22r

p ˆ   E  E ⋅ ejχ Polarization vector The polarization vector defines the polarization of the field (and also of the antenna) It is strictly related to the radiation vector M p ˆ =  E  E ⋅ ejχ = − j η 2λr  M t e− jβr r η 2λr  M t 1 r ⋅ ejχ =  M t  M t e − j βr+π 2 ( ) ⋅ ejχ   ⇒  p ˆ =  M t  M t = M ˆ t

Wavefront A wavefront is a locus where the field has constant phase e.g: E.0.)-F.(. Therefore the wavefront is defined by: arg(Eos)-Br=- If r is large and arg(E)is limited we have arg(Er)-Br≈-Br=-p→r= Therefore the wavefront is a spherical surface in our case.That's why it's called"spherical wave

Wavefront r Tx Ex (r,θ,ϕ) = E0 x (θ,ϕ) e− jβr r = E0 x r ej(arg(E0 x )−βr) A wavefront is a locus where the field has constant phase Therefore the wavefront is defined by: arg(E0 x ) − βr = −ϕ If r is large and arg(E0x) is limited we have arg(E0 x ) − βr ≈ −βr = −ϕ  ⇒  r = ϕ β Therefore the wavefront is a spherical surface in our case. That’s why it’s called “spherical wave”. e.g:

Spherical and plane waves spherical wavefront Spherical wave 下=ri (.6,p)=E。(0,p), In far field a spherical wave can be locally approximated with a Plane wave E(,0,p)≈E,e with E E(6,9 k=Bi, ≈plane wavefront

Spherical and plane waves Tx spherical wavefront Spherical wave  E(r,θ,ϕ) ≈  Eo (θ,ϕ) e− jβr r r = rˆ ir with  Eo ' =  Eo (θ,ϕ) r k = βˆ ir In far field a spherical wave can be locally approximated with a Plane wave  E (r,θ,ϕ) ≈  Eo ' e− j ki r ≈ plane wavefront k e

Definition of Ray (1/2) Given a propagating wave,every curve that is everywhere perpendicular to the wavefront is called electromagnetic ray.A ray is the path of the wavefront.There is a mutual identification btw wave and ray Therefore we assume that the ray also has a field,the field of the wave at every point

Definition of Ray (1/2) • Given a propagating wave, every curve that is everywhere perpendicular to the wavefront is called electromagnetic ray. A ray is the path of the wavefront. There is a mutual identification btw wave and ray • Therefore we assume that the ray also has a field, the field of the wave at every point