吉林大学：《计算机控制技术》课程教学资源（PPT课件讲稿）第七章 数字控制器的状态空间设计方法 7.5 状态观测器设计（2/2）

全维状态观测器 (4) 由前述可得 x(k+1)-(k+1)=Ax(k)+Bu(k)-(A-HC)(k)-Bu(k)-Hy(k) =(A-HC)[x(k)-(k)] 即 (k+1)=(A-HC)x(k) 若选怿合适的输出误差反馈矩阵日使得状态估计误 差系统的所有极点均位于z平面单位圆内，则误差可在 有限拍内趋于零，即状态估计值在有限拍内可以跟踪上 真实状态，且极点越靠近原点状态估计误差趋于零的速 度越快，反之越慢

全维状态观测器（4） 由前述可得 即 若选择合适的输出误差反馈矩阵H使得状态估计误 差系统的所有极点均位于z平面单位圆内，则误差可在 有限拍内趋于零，即状态估计值在有限拍内可以跟踪上 真实状态，且极点越靠近原点状态估计误差趋于零的速 度越快，反之越慢。 ( )[ ( ) ˆ( )] ( 1) ˆ( 1) ( ) ( ) ( ) ˆ( ) ( ) ( ) A HC k k k k A k B k A HC k B k Hy k x x x x x u x u = − − + − + = + − − − − ( ) ~ ( 1) ( ) ~ x k + = A − HC x k

全维状态观测器 (5) 若指定状态观测器的特征值为 21,22,‘,2m 即期望的特征方程为 f(2)=(2-1(z-22)…(z-z) =z”+(-10(2+22+…+z0)z”+…+(-1)”z12…2n=0 状态观测器的特征多项式为 (2)=2I-(A-HC)=0 比较两式两边z各次幂项的系数可得到一个元方程组，可求得输出 误差反馈系数矩阵H。 例7.8

全维状态观测器（5） * * * 1 2 , , , n z z z * * * * o 1 2 * * * 1 * * * 1 2 1 2 ( ) ( )( ) ( ) ( 1)( ) ( 1) 0 n n n n n n f z z z z z z z z z z z z z z z − = − − − = + − + + + + + − = f z zI A HC o ( ) ( ) 0 = − − = 若指定状态观测器的特征值为 即期望的特征方程为 状态观测器的特征多项式为 比较两式两边z各次幂项的系数可得到一个n元方程组，可求得输出 误差反馈系数矩阵H。 例7.8

2,降维状态观测器 己知n维系统是能观则的，其输出矩阵的秩是m,则 说明系统状态有m个是可以直接观则的，不需要对系统 的n个状态全部进行观测，而只需对另外n-m个状态进行 观测p回。即回用n-维状态观测器代替全维状态观测 器。这种维数低于被控系统状态向量的观测器称为降维 观测器。 >单输入多输出系统降维观测器的设计 已知n维线性定常离散系统(A,b,C)能观测 x(k+1)=Ax(k)+bu(k) y(k)=Cx(k) 其中，x()为n维状态向量，y(k)为m维输出列向量

2. 降维状态观测器（1） 已知n维系统是能观测的，其输出矩阵的秩是m，则 说明系统状态有m个是可以直接观测的，不需要对系统 的n个状态全部进行观测，而只需对另外n-m个状态进行 观测即可。即可用n-m维状态观测器代替全维状态观测 器。这种维数低于被控系统状态向量的观测器称为降维 观测器。 ➢ 单输入多输出系统降维观测器的设计 已知n维线性定常离散系统(A，b，C)能观测 其中，x(k)为n维状态向量，y(k)为m维输出列向量。 ( ) ( ) ( 1) ( ) ( ) k C k k A k bu k y x x x = + = +

降维状态观测器 (2 先将状态x()分解成两部分：可直接测量部分x(k)(mXI维)； 不能直接测量需重构部分x(k)(n-m)×1维)。即 += 色 (k)=[0 其中A1为(n-m)×(n-m)维；A12为(n-m)×m维；A21为m×(n-m)维； A22为m×(n-m)维；b1为(n-m)×1维，b2为m×1维。 x(k+1)=Ax(k)+42x2(k)+bu(k) x2(k+1)=A21x(k)+A22x2(k)+b2u(k) 为了用可直接观测的x()估计不可直接观测的x1(k)，引入一个虚 拟输出 (k)=A21x1(k)=x2(k+1)-A22x2(k)-b2u(k)

降维状态观测器（2） 先将状态x(k)分解成两部分：可直接测量部分x2 (k)(m×1维)； 不能直接测量需重构部分x1 (k)（(n-m)×1维）。即 其中A11为(n-m)×(n-m)维；A12为(n-m)×m维；A21为m×(n-m)维； A22为m×(n-m)维；b1为(n-m)×1维; b2为m×1维。 为了用可直接观测的x2 (k)估计不可直接观测的x1 (k) ，引入一个虚 拟输出 ( ) ( ) ( ) ( 1) ( 1) ( 1) 2 1 2 1 2 1 2 2 1 1 1 2 2 1 u k b b k k A A A A k k k        +             =      + + + = x x x x x       = ( ) ( ) ( ) [0 ] 2 1 k k k I x x y ( ) ( ) ( 1) ( ) ( ) 21 1 2 22 2 2 z k = A x k = x k + − A x k − b u k 1 11 1 12 2 1 x x x ( 1) ( ) ( ) ( ) k A k A k b u k + = + + 2 21 1 22 2 2 x x x ( 1) ( ) ( ) ( ) k A k A k b u k + = + +

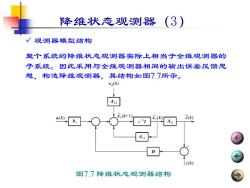
降维状态观测器 (3) 观测器模型结构 整个系统的降维状态观测器实际上相当于全维观侧器的 子系统。因此采用与全维观测器相同的输出误差反馈思 想，构造降维观测器，其结构如图7.7所示。 x2() A12 H(k x() 2) z1 A21 H z() 图77降维状态观测器结构

降维状态观测器（3） ✓ 观测器模型结构 整个系统的降维状态观测器实际上相当于全维观测器的 子系统。因此采用与全维观测器相同的输出误差反馈思 想，构造降维观测器，其结构如图7.7所示。 图7.7 降维状态观测器结构

降维状态观测器 (4) 观测器方程为 x(k+1)=A1x(k)+A12x2(k)+bu(k)+H[z(k)-(k)] =(A11-HA21)x1(k)+A12x2(k)+b4(k)+H(k) k)=42(k) 令观测器状态误差为 x( 划 x()=x(2)-x(E) 同全维观测器情况类似，因为 x(k+1)=A1(k)+A2x2(k)+bu(k)且(k)=A21飞(k Dx(k+1)=x(k+1)-(k+1) =Ax(k)+A2x2()+b,u(k)-(A1-HA2)x(2)-A2x2(k)-b,u(k)-Hz(k) =(A1-HA2i[x(k)-x(k】 =(A1-HA2)x()

降维状态观测器（4） 观测器方程为 令观测器状态误差为 同全维观测器情况类似，因为 ( ) ˆ ( ) ( ) ( ) ( ) ˆ ( 1) ˆ ( ) ( ) ( ) [ ( ) ˆ( )] 1 1 2 1 1 1 2 2 1 1 1 1 1 1 2 2 1 A HA k A k b u k H k k A k A k b u k H k k x x z x x x z z = − + + + + = + + + − ˆ( ) ˆ ( ) 21 1 z k = A x k = − 1 1 1 x x x ( ) ( ) ( ) k k k ˆ + = + − + = + + − − − − − = − − = − 1 1 1 11 1 12 2 1 11 21 1 12 2 1 11 21 1 1 11 21 1 ( 1) ( 1) ( 1) ˆ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ˆ ( )[ ( ) ( )] ˆ ( ) ( ) k k k A k A k b u k A HA k A k b u k H k A HA k k A HA k x x x x x x x z x x x 1 11 1 12 2 1 x x x ( 1) ( ) ( ) ( ) k A k A k b u k + = + + 21 1 且 z x ( ) ( ) k A k =

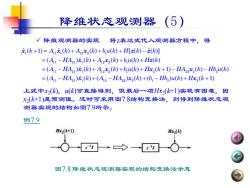
降维状态观测器 (5) 降维观测器的实现 将Z表达式代入观测器方程中，得 x(k+1)=A,x(k)+A2x2(R)+bu(k)+H[z(k)-2()] =(A1-HA21)()+A2x2(k)+b,u(k)+Hz() =(A1-HA21)x(®)+A12x2()+b,u(k)+Hx2(k+1)-HA22x2()-Hb2u(k) =(A-HA2)x(k)+(A2-HA2)x2(k)+(b-Hb2)u(k)+Hx2(k+1) 上式中x2(k),(k)可直接得到，但最后一项HX2(k什1)实现有困难，因 x2(k什1)是预测值。这时可采用图7.8结构变换法，则得到降维状态观 测器实现的结构如图7.9所示。 例7.9 Hx2(k+1) 丑2() 图78降维状态观测器实现的结构变换法示意

降维状态观测器（5） + = + + + − = − + + + = − + + + + − − = − + − + − + + 1 11 1 12 2 1 11 21 1 12 2 1 11 21 1 12 2 1 2 22 2 2 11 21 1 12 22 2 1 2 2 ˆ ( 1) ( ) ( ) ( ) [ ( ) ( )] ˆ ˆ ( ) ( ) ( ) ( ) ( ) ˆ ( ) ( ) ( ) ( ) ( 1) ( ) ( ) ˆ ( ) ( ) ( ) ( ) ( ) ( ) ( ˆ k A k A k b u k H k k A HA k A k b u k H k A HA k A k b u k H k HA k Hb u k A HA k A HA k b Hb u k H k x x x z z x x z x x x x x x x 1) ✓ 降维观测器的实现 将z表达式代入观测器方程中，得 上式中x2 (k)，u(k)可直接得到，但最后一项Hx2 (k+1)实现有困难，因 x2 (k+1)是预测值。这时可采用图7.8结构变换法，则得到降维状态观 测器实现的结构如图7.9所示。 例7.9 图7.8 降维状态观测器实现的结构变换法示意