《计算机科学》相关教学资源（PPT课件讲稿）On the Relationship between Concurrent Separation Logic and Assume-Guarantee Reasoning

On the Relationship Between Concurrent Separation Logic and Assume-Guarantee Reasoning Xinyu Feng Yale University Joint work with Rodrigo Ferreira and Zhong Shao

On the Relationship Between Concurrent Separation Logic and Assume-Guarantee Reasoning Xinyu Feng Yale University Joint work with Rodrigo Ferreira and Zhong Shao

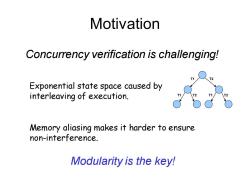
Motivation Concurrency verification is challenging! Exponential state space caused by interleaving of execution. Memory aliasing makes it harder to ensure non-interference. Modularity is the key!

Motivation Concurrency verification is challenging! T1 T1 T1 T2 T2 T2 Exponential state space caused by interleaving of execution. Memory aliasing makes it harder to ensure non-interference. Modularity is the key!

Two kinds of modularity 。Control modularity -a.k.a.thread-modularity each thread is verified independently of others 。Data modularity -a.k.a.information hiding -each thread only cares about data it uses

Two kinds of modularity • Control modularity – a.k.a. thread-modularity – each thread is verified independently of others • Data modularity – a.k.a. information hiding – each thread only cares about data it uses

Existing work Assume-Guarantee (A-G)reasoning [Misra&Chandy'81,Jones'83] ©thread modularity general:no restriction over synchronization pattern spec of A&G requires global data invariants Concurrent Separation Logic (CSL)[o'Hearn,Brookes 20041 ©thread modularity data modularity:local reasoning restrictive synchronization pattern shared resources can be accessed only inside critical regions

Existing work • Assume-Guarantee (A-G) reasoning [Misra&Chandy’81, Jones’83] ☺ thread modularity ☺ general: no restriction over synchronization pattern  spec of A&G requires global data invariants • Concurrent Separation Logic (CSL) [O’Hearn, Brookes 2004] ☺ thread modularity ☺ data modularity: local reasoning  restrictive synchronization pattern shared resources can be accessed only inside critical regions

Our Contributions SAGL:combining CSL and A-G reasoning - extend A-G logic with local reasoning better data modularity (than A-G reasoning) thread modularity no restriction over synchronization pattern A formal study of the relationship between CSL and A-G reasoning

Our Contributions • SAGL: combining CSL and A-G reasoning – extend A-G logic with local reasoning ☺ better data modularity (than A-G reasoning) ☺ thread modularity ☺ no restriction over synchronization pattern • A formal study of the relationship between CSL and A-G reasoning

Outline of this talk 。Background Concurrent Separation Logic -Assume-Guarantee reasoning SAGL:combination of CSL A-G reasoning Interpretation of CSL in SAGL

Outline of this talk • Background – Concurrent Separation Logic – Assume-Guarantee reasoning • SAGL: combination of CSL & A-G reasoning • Interpretation of CSL in SAGL

Concurrent Separation Logic Assertions capture ownerships of resources 1→n Cannot access resource without ownership ● Shared resources are protected by critical regions (CRs) Transfer of ownership at boundary of CR

Concurrent Separation Logic • Assertions capture ownerships of resources • Cannot access resource without ownership • Shared resources are protected by critical regions (CRs) • Transfer of ownership at boundary of CR l  n

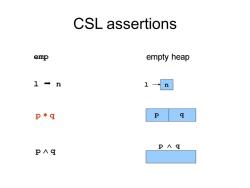
CSL assertions emp empty heap 1→1 n 1→ n p*q P g P∧g P∧g

CSL assertions l  n l n p  q p q emp empty heap p  q p  q

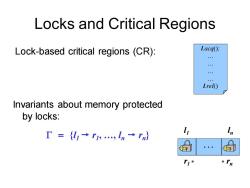
Locks and Critical Regions Lock-based critical regions (CR): Lacq(); Lrel() Invariants about memory protected by locks: Γ={化→，ln→rn} 1* *In

Locks and Critical Regions Lock-based critical regions (CR): l.acq(); … … … … l.rel() Invariants about memory protected by locks:  = {l1  r1 , …, ln  rn } r1   rn . . . l1 ln

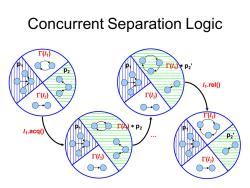
Concurrent Separation Logic T4) E()p2' P2 1.rel() T(2) *p2 1.acq() T(2)

p1 (l2 ) p2  (l1 ) p1 (l2 ) (l1 )  p2  Concurrent Separation Logic p1 (l2 ) p2 (l1 ) l1 .acq() l1 .rel() … p1 (l2 ) (l1 )  p2