《物理化学》课程教学资源(习题解答)第三章 统计热力学

第三章统计热力学复习题及参考答案 1.混合晶体是由晶格点阵中随机放置Nc个C分子和D分子组成的。 ①证明分子能够古据格点的花样为甲-c十,若。=N。一,利用斯转林公式证明 NeINp! W=2N (2)若Nc=N。=2,利用上式计算得W=2=16,但实际上只能排出6种花样,究竞何者正确?为 什么? 解:(1)证明:取(Nc+N。)的全排列,则总共排列的花样数为(Nc+N。)1种,现Nc个相同的C和 N。个相同的D.故花样数为W=,+。当Ne=N。=N时 Ne!Np! (N+N) W= N! 兮5兮r 取自然对数: In-InMt-2IjN)-NInN-N-2NInN)-N]-NInN-N-NIN)+N -NInN-NIn(-N)=NInN-NIn-NInN-NIn-NIn2-In2* :.W=2w (2)实际排出6种花样是正确的,因为Stirling是一个近似公式适用于N很大时才误差较小。而在N 为4时,用W=2来计算就会产生较大误差。 2.(1)设有三个穿绿色、两个穿灰色和一个穿蓝色制服得军人一起列队,试问有多少种对型?现设穿 绿色制服得可有三种肩章并任取其中一种佩带,穿灰色制服的可有两种肩章,而穿蓝色的可有两种肩章, 试列出求算队型数目的公式。 Q)试证明含有N个子的定位体系。某种分在,的微酸状态数为L,=NΠ受号〈鱼为相应的简并 度) 答:(1)取6个不同的全排列,应有6!种花样,但其中3种完全相同互换位置不能导致新花样另两
第三章 统计热力学 复习题及参考答案 1.混合晶体是由晶格点阵中随机放置 NC个 C 分子和 D 分子组成的。 (1) 证明分子能够占据格点的花样为 ! ! ( )! C D C D N N N N W ,若NC N D N 2 1 ,利用斯特林公式证明 N W 2 (2) 若NC N D 2,利用上式计算得 4 W 2 =16,但实际上只能排出 6 种花样,究竟何者正确?为 什么? 解:(1)证明:取( ) NC N D 的全排列,则总共排列的花样数为( )! NC N D 种,现NC 个相同的 C 和 N D 个相同的 D。故花样数为 ! ! ( )! C D C D N N N N W 当NC N D N 2 1 时 2 )!] 2 1 [( ! )! 2 1 )!( 2 1 ( )! 2 1 2 1 ( N N N N N N W 取自然对数: N N N N N N N N N N N N W N N N N N N N N N N N N N N ln 2 ln 2 2 1 ln ln 2 1 ) ln ln 2 1 ln ln( ) 2 1 ] ln ln( 2 1 ) 2 1 ln( 2 1 )! ln 2[ 2 1 ln ln ! 2ln( N W 2 (2)实际排出 6 种花样是正确的,因为 Stirling 是一个近似公式适用于 N 很大时才误差较小。而在 N 为 4 时,用 4 W 2 来计算就会产生较大误差。 2.(1)设有三个穿绿色、两个穿灰色和一个穿蓝色制服得军人一起列队,试问有多少种对型?现设穿 绿色制服得可有三种肩章并任取其中一种佩带,穿灰色制服的可有两种肩章,而穿蓝色的可有两种肩章, 试 列出求算队型数目的公式。 (2)试证明含有 N 个粒子的定位体系,某种分布- x t 的微观状态数为 ! ! i N i x N g t N i (gI为相应的简并 度) .答:(1)取 6 个不同的全排列,应有 6!种花样,但其中 3 种完全相同互换位置不能导致新花样另两

616x5×4×3×2 种完全相酮同样这2种相同物种的全排列为2!种)放排列花样数为:一32×12=60 称品另种机有种这3排列为3取6个不的全排返共61种花 穿绿色制服3个人有3种肩章,任取一种佩带,相当于有简并度为5(g,)。就有3种花样。穿灰色 的有两种肩章相当于简并度为2,就有2种而穿蓝色的有4种肩章相当于简并度为g,=4就有4种, 但其中有3个穿绿色制服的戴相同肩章,总共有3!种花样,2个穿灰色的戴相同肩章有2!种 62兴-60x27x44=250么=N N (2)在N个不同粒子中取出N1个粒子放在,中,其放法为C种。在6,能级上有g1个不同状态, 故在6,上总共有gC心种放法,同理在从(NN,)中取出N个粒子放在e2上的放法为gCx种 放法。所以这种分布的微观状态数: 1=gMCNgCNEN BCNN-NA N (N-N) (N-N-N2)! NIN-N I NICN-N-N.NCN-N-N.-N. =品- NI 3.在公园的猴舍中陈列着三个金丝猴和两种长臂猿,金丝猴有红、绿两种帽子,仍戴一种,而长臂猿 可在黄、灰和黑中选戴一种,试问陈列时间可出现几种不同的情况,并列出求算公式。 解:设N3,2,而g2,3则W=W+8-L.,+8-6+2-0.2+3-24 V(81-1!N2(g2-1!3(2-11213-1)1 种, 因为每一种动物必须戴:三个金丝猴:(红、红、红)(绿、绿、绿)(红、红、绿)(绿、绿、红)共 4种。两种长臂猿:(黑、黑)(灰、灰)(黄、黄)(黑、灰)(黄、灰)(黑、黄).共6种。总共为4×6=24 种。 4.已知对排定位体系QU,M)=M匀 Nm8试证明武324,325)和(326
种完全相同(同样这 2 种相同物种的全排列为 2!种)故排列花样数为: 60 3 2 1 2 1 6 5 4 3 2 3!2!1! 6! W 种, ! ! ! i i T N N t 另一种只有一种这 3 种的全排列为 3!种,取 6 个不同的全排列总共有 6!种花样,而 穿绿色制服 3 个人有 3 种肩章,任取一种佩带,相当于有简并度为 5( N gi )。就有 33 种花样。穿灰色 的有两种肩章相当于简并度为 2,就有 22 种而穿蓝色的有 4 种肩章相当于简并度为 4 N gi 就有 41 种, 但其中有 3 个穿绿色制服的戴相同肩章,总共有 3!种花样,2 个穿灰色的戴相同肩章有 2!种 60 27 4 4 25920 3!2!1! 6!3 2 4 3 2 1 ! ! i N i x N g t N i (2)在 N 个不同粒子中取出 N1个粒子放在 1 中,其放法为 N1 CN 种。在 1 能级上有 g1个不同状态, 故在 1 上总共有 1 1 1 N N N g C 种放法,同理在从(N-N1)中取出 N2个粒子放在 2 上的放法为 2 1 2 2 N N N N g C 种 放法。所以这种分布的微观状态数: ! ! ! ( ) !( )! ( )! !( )! ( )! !( )! ! 3 1 2 3 1 2 3 2 1 2 1 2 1 1 1 1 2 3 1 2 3 3 1 2 2 3 1 1 1 2 i N i i N i N N N N N N N N N N N N N N N N g N N N g N N N N N N N N g N N N N N N g N N N N g t g C g C g C i i 3.在公园的猴舍中陈列着三个金丝猴和两种长臂猿,金丝猴有红、绿两种帽子,仍戴一种,而长臂猿 可在黄、灰和黑中选戴一种,试问陈列时间可出现几种不同的情况,并列出求算公式。 解:设 N1=3,N2=2,而 g1=2,g2=3 则 24 2!(3 1)! (2 3 1)! 3!(2 1)! (3 2 1)! !( 1)! ( 1)! !( 1)! ( 1)! 2 2 2 2 1 1 1 1 N g N g N g N g W 种, 因为每一种动物必须戴:三个金丝猴:(红、红、红)(绿、绿、绿)(红、红、绿)(绿、绿、红)共 4 种。两种长臂猿:(黑、黑)(灰、灰)(黄、黄)(黑、灰)(黄、灰)(黑、黄)。共 6 种。总共为4 6 24 种。 4.已知对非定位体系 N U N N i N i i i i i N g N N U V N ! ! ! 1 ( , , ) 试证明式(3.24),(3.25)和(3.26)

解对定位休系口-公m的(第怎的猫果) 对定位体系n-2=2Π宁-n 物最大项原星。=N加(定位体系 对花位体系-n号n-ng-2》-∑Nng-∑n+N 微分:20'-ng-nN-NaL+1-ng,-a-h是 ON; ON: 用拉格朗日乘因子法,求得:(书中189页) 8+a+肠=0,即n是+a+度=0,是-t,= aN eE8e5’2X-28e=w,e∑8e=w ek&e房 iN=ge'ch =N ge 、高·=冬音与定位体家的爱兹安分布公 式相同 In.=∑ng-∑hN,=∑,hg,-∑N,lnN,+∑N,-∑N,h是+N(∑N,=M M8净+-义之c净 =∑N,ln& e音+W-2Wn2e音-ΣViMe品+N ∑&,e帝 =ln∑8,e)-∑N,lhN-∑Nine音+N=lnEg,e备y-lnNm∑Ns :L-n②2产,号 N
解:对定位体系: ) ! ( ! i N i i N g t N i (第二题的结果) 对非定位体系: ! ) ! ( ! ! 1 i N i i N i i N g N g N N t i i 摘取最大项原理: ! ! i N i m N g t N i (定位体系) ! ! ! ! 1 i N i i N i m N g N g N N t i i 对非定位体系: !i N i m N g t i i i i i i i N ln t ln gi i ln(N !) N ln g N ln N N 微分: i i i V i i i i i i N g g l N N N N g N N t 1 ln ln ln ln ln ln ln 用拉格朗日乘因子法,求得:(书中 189 页) 0 ln * i Ni t ,即ln 0 * i i V N g , i e N g i V * , i N g e i i * i g e N e i , Ni gi e i N * , e gi e i N , kT i kT i V i i i i i i i i g e g e N g e g e N g e e N * , kT i kT i i i i g e g e N N * 与定位体系的玻兹曼分布公 式相同 kT U N g e kT U g e N kT N g e N N N e N g e N N N g e N Ne N Ne g e N N g e g e N g N N N N N g t g N N g N N N N kT N N i kT i N v kT i kT i i kT N i kT i kT i i kT kT i i kT v kT i i i i i i i V i i i i i N m i i i i i i i i i i i i i ! ( ) ln( ) ln ! ln ln( ) ln ln ln( ) ln ! ln( ) ln ln ln( ) ln ln ln ln ln ln ( ) S 非 T U N g e k k t k kT N v m i ! ( ) ln ln ln

F:U-=U-灯ngy-U:-灯n&ey N! N! 5.试证明玻兹曼分布的微观状态数公式为n1=ng,e西)式中q=∑8,ep(-行,U-∑X,6 证:利用定位体系任意分配方式公式:【=NS(玻益曼统计是指经典统计认为粒了是可区别的。 N! 即定位体系) 取自然对数:lnt=lnN+∑ng-∑lnN 对最概然分布: Intn=ln+∑lng,'-∑lnN=WlnN+∑Nng,-∑NnN w+∑In(总)=NinN+∑NIn是) ∑8&e岛 =NnN+∑n∑&e e =NinW+∑Nn∑g,e音-∑NinN-∑NIne音 -D2e帝+2N后=Nn2se立+岩=Nng+后=hg+号 =lng'+lnea=lng'.e可) .Int In(ge) W=.8e音 上品c凉 6.设有一圆柱形铁皮筒,体积为V。=R2L=1.00dm铁皮面积为S=2πR2+2πRL,试用拉格朗日乘 因子法当铁皮面积为最小时,圆柱半径(R)和高(L)之间的关系?并算出至少要消耗多少面积的铁 皮? 不讨论(可自己求解) 解:L=R 5-2a成+2=2a成+后0m1-1-
F 非 ! ( ) ln ! ( ) ln N g e U kT N g e U TS U kT kT N v kT N v i i 5.试证明玻兹曼分布的微观状态数公式为ln ln( ) kT U N t q e 式中 i i i kT q g exp( ) ,U Ni i 证:利用定位体系任意分配方式公式: ! ! i N i N g t N i (玻兹曼统计是指经典统计认为粒子是可区别的, 即定位体系) 取自然对数:ln ln !ln ln ! i N t N gi i N 对最概然分布: kT i i kT i i kT kT i i kT i kT i i i i i i i i i i i N m i i i i i i i i N N N g e N N N e Ne g e N N N g e g e N g N N N N g N N N t N g N N N N g N N ln ln ln ln ln ln ln ln( ) ln ln( ) ln ln ! ln ln ! ln ln ln * * * * * * * * * * * * ln ln ln( ) ln ln ln ln * * kT U kT N U N kT N i i i kT i i q e q e kT U q kT U N q kT U N g e kT N g e N i i ln ln( ) kT U N m t q e ( ) * kT i kT i i i i g e g e N N 6.设有一圆柱形铁皮筒,体积为 2 3 V0 R L 1.00dm 铁皮面积为S 2R 2RL 2 ,试用拉格朗日乘 因子法当铁皮面积为最小时,圆柱半径(R)和高(L)之间的关系?并算出至少要消耗多少面积的铁 皮? 不讨论(可自己求解) 解: 2 1 R L ) 1 ( 1 2 2 2 2 2 2 2 R R L RL R S R RL R

极值时R=4成-后=04-2=0R=名R=(层 :L=2R(圆柱半径R与高之间的关系) s-2减+32m+m6=6a2=6a1a,54a 2 设:fR)=2aR+2R,gR)=RL-l,F(RL)=fR0+g(RD -2πR2+2πRL+1(πR2L-l) (0a=4aR+2l+2R=0 (1) (党u2成+R-0 (2) 0.l-10 (3) 由(2)2R+R2=0R(2+2R=0 R=-2 (4) (4)代入(1),4πR+2l+2πR×(-2)=0,6πR-2l=0L=2R S=2πR2+2πRL-2πR2+4πR2-6πR2=0.554(dm2) ==球e=2a-1R=E=0s2 7.试用配分函数表示出单原子理想气体的吉布斯自由能G和焓H 答:理想气体为非定位体系:对单元子分子,只有电子核和平动配分函数。 F-kTTg-KTg.GU+PV-FPV x=,《oN!为数。,gr与体积无关) P-郎 G=F+=-tnh号-nngi-ioi+n2a2n
极值时: 0 2 4 2 R R dR dS 0 4 2 3 R 4 3 2 R 3 1 ) 4 2 ( R 3 1 3 2 2 ) 4 2 2( ) 4 2 ( 1 1 R L L 2R (圆柱半径 R 与高之间的关系) 3 2 2 3 2 2 2 2 2 ) 5.54 4 3.14 2 ) 6 3.14 ( 4 2 S 2 R 2 RL 2 R 4 R 6 R 6 ( dm 设: f (R, L) 2R 2RL 2 , ( , ) 1 2 g R L R L , 2 2 ( 1) ( , , ) ( , ) ( , ) 2 2 R RL R L F R L f R L g R L ( ) 4 2 2 0 R L RL R F l (1) ( ) 2 0 2 R R L F R (2) ( ) 1 0 2 R L F RL (3) 由(2) 0 2 2 R R R(2 R) 0 R 2 (4) (4)代入(1),4R 2L 2R (2) 0 , 6R 2L 0 L 2R 2 2 2 4 6 0.554( ) 2 2 2 2 2 S R RL R R R dm 由 (2 ) 2 1 2 2 3 V0 R L R R R 0.542 2 1 3 R 7.试用配分函数表示出单原子理想气体的吉布斯自由能 G 和焓 H。 答:理想气体为非定位体系:对单元子分子,只有电子核和平动配分函数。 N n N e N t N kT q kT q N q kT N q F kT ln ln ! ln ! ln , G U PV TS F PV , T N t T N V q NkT V F P ) ln ( ) ( , ( N !为常数。 e n q ,q 与体积无关) T N N t n N e N t V q kT q kT q NkT N q G F PV kT ) ln ln ln ( ! ln H U PV , F U TS , V N T F T F U S ( ) 2 2 2 2 2 ( ) 1 ( ) , 1 T U T F T F T T U T F T F U T F T V N V N

品。片人吉布斯-安姆霍兹公式 U=-T21]w=-T2 th器-hg-ing2 OT NT nd aT IPMr &Q0,气体可作为座想气体,并设其各个自由度都限从经真的能量的分原理、已知7一号。15试用 计算方法判断CO2是否为线性分子。 解215C15 (第一章中讨论到理想气体Cm=Cm+R) C.R1C.015CR.C 设:若C02为线性分子,补:平动有3个自由度。根据其总自由度为3如。∴振动自由度应为 3m-3-2=3×3-3-2=4。由于一个振动的能量中的表达式中包括2个平方项(83页小字部分), 振动的动能和振动的位能,每个平方项都提供kT的能量(若为1ol。则为二kT)若一个分子有七 个平动自由度,「个转动自由度。S个振动自由度。则:总能量6=0+r+2s)7, C=0-0*r+2。 :.Cm=(+r+2s)R 若C02为线性分子 C=+r+20n-1-rR=B+2+26x3-3-2R-=号 与原来题中给的条件求出的Cm一致。故假设正确,C02是直线型分子。 9.四种分子的有关参数如下:
2 ] ( ) [ T U T T F V N 吉布斯─亥姆霍兹公式 V N t V N N n N e N t V N T q NkT T k q k q N q k T T T F U T ) ln ] ( ln ln ) ! ( ln ] [ ( ) [ 2 2 2 T N t V N t T q NkTV T q H U PV NkT ) ln ) ( ln ( 2 8.CO2气体可作为理想气体,并设其各个自由度都服从经典的能量均分原理,已知 1.15 v p C C 试用 计算方法判断 CO2是否为线性分子。 解:由 1.15 v m p m C C 1.15 v m v m C C R (第一章中讨论到理想气体Cpm Cvm R ) Cv m R 15Cv.m 1. . 0.15Cvm R . Cv m R R 2 13 0.15 1 设:若 CO2 为线性分子,补:平动有 3 个自由度。根据其总自由度为 3n。∴振动自由度应为 3n 3 2 3 3 3 2 4。 由于一个振动的能量中的表达式中包括 2 个平方项(83 页 小字部分), 振动的动能和振动的位能,每个平方项都提供 kT 2 1 的能量(若为 1mol。则为 kT 2 1 )若一个分子有七 个平动自由度,r 个转动自由度。S 个振动自由度。则:总能量 (t r 2s)kT 2 1 , t r s k T U Cv ( 2 ) 2 1 ( ) 。 Cv m (t r 2s)R 2 1 若 CO2为线性分子 Cv m t r n t r R R R 2 13 [3 2 2(3 3 3 2)] 2 1 [ 2(3 )] 2 1 . 与原来题中给的条件求出的Cvm一致。故假设正确,CO2是直线型分子。 9.四种分子的有关参数如下:

分子 @'k 出 2 87.5 5976 HBr 81 122 3682 28 2.89 3353 C 71 0.35 801 问在同温同压下,那种气体的摩尔平动熵最大?那种气体的摩尔转动熵最大?那种气体的转动基本频率 最小? 解:先写出平动熵,转动嫡及振动特征温度的表达式: s=4号+=h2+ Nh3 (沙克尔特鲁德公式)Og=(2mk虹).v=2mky=2mkDy h2 (h2)2 -+限里为1型L从-足 由公式可见,粒子的质量m越大,平动熵则越大,所以HB,的摩尔嫡最大。 F=U-N5=号+号U=7(2F-h 5h号+Nn-ng-nAn2 oIn 8x'lkT N&Ing-kin NNkT(ng )yx NkIn-kIn NH+NKT( 2 .M 0n8r+h刀 5'+=NkIn I NNKT( 一=n8=-hM4话 动2 02 0动2 双原子分千:q.) 0h2 .S"sm=kIng'+k-k(6.02x102)In N+Nk =kIng'+k-kInL+k=k(Ing'-InL+2)
问在同温同压下,那种气体的摩尔平动熵最大?那种气体的摩尔转动熵最大?那种气体的转动基本频率 最小? 解:先写出平动熵,转动熵 及振动特征温度的表达式: ] 2 (2 ) 5 ] [ln 2 5 [ln 3 2 3 V Nh mkT Nk N q S Nk t t (沙克尔—特鲁德公式) V h mkT V h mkT V h mkT qt 3 2 3 2 3 2 2 3 2 3 2 (2 ) ( ) (2 ) ) 2 ( ( ] 2 (2 ) 5 [ln 3 2 3 m t m V Lh mkT S R (物质量为 1mol. N L. Lk R V Vm) 由公式可见,粒子的质量 m 越大,平动熵则越大,所以 HBr的摩尔熵最大。 F U TS T U T F S V N T q U NkT ) ln ( 2 ! ln N q F kT N S 非 V N V N N T q Nk q k N NkT T q NkT N q k ) ln ) ln ln ! ( ln ( ! ln r S 非 k N Nk H T Nk k N Nk h IkT Nk T T h Ik k N NkT h IkT Nk T h IkT k N NkT h IkT Nk T q Nk q k N NkT r V N V N V N r r ln ln ! ln ! 8 ) ln ln ) 8 (ln ln ! ( 8 ln ) 8 ln ln ! ( 8 ) ln ln ln ln ! ( 2 2 2 2 2 2 2 2 2 2 (双原子分子: 2 2 8 h IkT qr ) r S 非m ln (6.02 10 )ln ln ln (ln ln 2) 23 k q k k N Nk k q k k L k k q L r r r 分子 Mt Θr /k Θv /k H2 2 87.5 5976 HBr 81 12.2 3682 N2 28 2.89 3353 Cl2 71 0.35 801
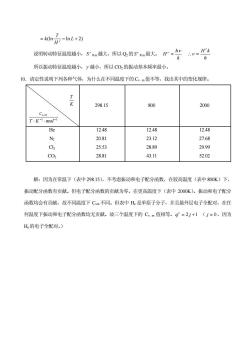
=kn不-nL+2) 说明装征温度越小、S越大所以Q的Sn大。H-贺- 所以振动特征温度越小,Y越小,所以CO2的振动基本频率最小。 10.请定性说明下列各种气体,为什么在不同温度下的C.m值不等,找出其中的变化规律。 298.15 800 2000 CvM T·K-l·mol He 12.48 12.48 12.48 N2 20.81 23.12 27.68 Cl2 25.53 28.89 29.99 C02 28.81 43.11 52.02 解:因为在常温下(表中298.15),不考虑振动和电子配分函数,在较高温度(表中800K)下, 振动配分函数有贡献。但电子配分函数的贡献为零。在更高温度下(表中2000水)。振动和电子配分 函数均会有贡献,故不同温度下Cm不同。但表中H。是单原子分子,并且最外层电子全配对,在任 何温度下振动和电子配分函数均无贡献。故三个温度下的C.m值相等。g=2j+1(=0,因为 H的电子全配对。)
(ln ln L 2) H T k r 说明转动特征温度越小, r S 非m越大,所以 Q2的 r S 非m最大。 k h H r h H k r 所以振动特征温度越小, 越小,所以 CO2的振动基本频率最小。 10.请定性说明下列各种气体,为什么在不同温度下的 Cv,m值不等,找出其中的变化规律。 K T 1 1 , T K mol cv M 298.15 800 2000 He 12.48 12.48 12.48 N2 20.81 23.12 27.68 Cl2 25.53 28.89 29.99 CO2 28.81 43.11 52.02 解:因为在常温下(表中 298.15),不考虑振动和电子配分函数,在较高温度(表中 800K)下, 振动配分函数有贡献。但电子配分函数的贡献为零。在更高温度下(表中 2000K)。振动和电子配分 函数均会有贡献,故不同温度下 Cvm 不同。但表中 He 是单原子分子,并且最外层电子全配对,在任 何温度下振动和电子配分函数均无贡献。故三个温度下的 Cv,m 值相等。q 2 j 1 e ( j 0,因为 He的电子全配对。)
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《物理化学》课程教学资源(习题解答)第一章 热力学第一定律及其应用.pdf
- 新疆大学:《物理化学》课程授课教案(讲义)第十章 电解与极化作用.doc
- 新疆大学:《物理化学》课程授课教案(讲义)第十四章 胶体分散系统和大分子溶液.doc
- 新疆大学:《物理化学》课程授课教案(讲义)第十二章 化学动力学基础(二).doc
- 新疆大学:《物理化学》课程授课教案(讲义)第十三章 表面物理化学.doc
- 新疆大学:《物理化学》课程授课教案(讲义)第十一章 化学动力学基础(一).doc
- 新疆大学:《物理化学》课程授课教案(讲义)第八章 电解质溶液.doc
- 新疆大学:《物理化学》课程授课教案(讲义)第九章 可逆电池和可逆电极.doc
- 新疆大学:《物理化学》课程授课教案(讲义)第七章 统计热力学初步.doc
- 新疆大学:《物理化学》课程授课教案(讲义)第四章 多组分系统热力学及其在溶液中的应用.doc
- 新疆大学:《物理化学》课程授课教案(讲义)第六章 化学平衡.doc
- 新疆大学:《物理化学》课程授课教案(讲义)第五章 相平衡.doc
- 新疆大学:《物理化学》课程授课教案(讲义)第二章 热力学第一定律.doc
- 新疆大学:《物理化学》课程授课教案(讲义)第三章 热力学第二定律.doc
- 新疆大学:《物理化学》课程授课教案(讲义)第一章 气体(主讲:刘月娥).doc
- 新疆大学:《物理化学》课程教学大纲 Physicalchemistry(理科).doc
- 新疆大学:《物理化学》课程教学大纲 Physical chemistry(工科).doc
- 新疆大学:《物理化学》课程教学大纲 Physical chemistry(48学时).doc
- 新疆大学:《物理化学》课程实验大纲 Experiments in Physical Chemistry.doc
- 新疆大学:《物理化学》课程教学大纲 Physicalchemistry(64学时).doc
- 《物理化学》课程教学资源(习题解答)第二章 热力学第二定律.pdf
- 《物理化学》课程教学资源(习题解答)第五章 相平衡.pdf
- 《物理化学》课程教学资源(习题解答)第四章 多组分系统热力学.pdf
- 《物理化学》课程教学资源(习题解答)第七章 电解质溶液.pdf
- 《物理化学》课程教学资源(习题解答)第九章 电解与极化作用.pdf
- 《物理化学》课程教学资源(习题解答)第八章 可逆电池的电动势及其应用.pdf
- 《物理化学》课程教学资源(习题解答)第六章 化学平衡.pdf
- 《物理化学》课程教学资源(习题解答)第十一章 动力学基础(二).pdf
- 《物理化学》课程教学资源(习题解答)第十二章 界面现象.pdf
- 《物理化学》课程教学资源(习题解答)第十章 动力学基础(一).pdf
- 南京大学:《物理化学》课程教材电子教案(PPT教学课件,第五版)第10章 电解与极化.pps
- 南京大学:《物理化学》课程教材电子教案(PPT教学课件,第五版)第11章 化学动力学基础(一).pps
- 南京大学:《物理化学》课程教材电子教案(PPT教学课件,第五版)第12章 化学动力学基础(二).pps
- 南京大学:《物理化学》课程教材电子教案(PPT教学课件,第五版)第13章 表面物理化学.pps
- 南京大学:《物理化学》课程教材电子教案(PPT教学课件,第五版)第14章 胶体分散系统.pps
- 南京大学:《物理化学》课程教材电子教案(PPT教学课件,第五版)第01章 气体.pps
- 南京大学:《物理化学》课程教材电子教案(PPT教学课件,第五版)第02章 热力学第一定律.pps
- 南京大学:《物理化学》课程教材电子教案(PPT教学课件,第五版)第03章 热力学第二定律.pps
- 南京大学:《物理化学》课程教材电子教案(PPT教学课件,第五版)第04章 多组分系统热力学及其在溶液中应用.pps
- 南京大学:《物理化学》课程教材电子教案(PPT教学课件,第五版)第05章 相平衡.pps
