香港中文大学：《CMSC5719 Seminar》课程教学资源（讲义）Lecture 02 Game theory in computer science

Game theory in computer science Shengyu Zhang The Chinese University of Hong Kong

Shengyu Zhang The Chinese University of Hong Kong

Map Intro to strategic-form games aTwo forms Examples oNE and CE Algorithmic questions in games Hardness of finding an NE and CE Congestion games Game theory applied to computer science

Map ◼ Intro to strategic-form games ❑ Two forms ❑ Examples ❑ NE and CE ◼ Algorithmic questions in games ❑ Hardness of finding an NE and CE ❑ Congestion games ◼ Game theory applied to computer science

Part I.strategic-form games

Part I. strategic-form games

Game:Two basic forms SCISSORS strategic (normal)form extensive form

Game: Two basic forms strategic (normal) form extensive form

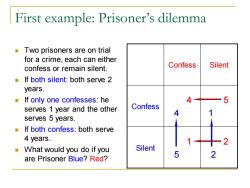
First example:Prisoner's dilemma Two prisoners are on trial for a crime,each can either confess or remain silent. Confess Silent If both silent:both serve 2 years. If only one confesses:he 4 5 serves 1 year and the other Confess 4 serves 5 years. If both confess:both serve 4 years. 2 What would you do if you Silent are Prisoner Blue?Red? 5 2

First example: Prisoner’s dilemma ◼ Two prisoners are on trial for a crime, each can either confess or remain silent. ◼ If both silent: both serve 2 years. ◼ If only one confesses: he serves 1 year and the other serves 5 years. ◼ If both confess: both serve 4 years. ◼ What would you do if you are Prisoner Blue? Red? Confess Silent Confess 4 4 5 1 Silent 1 5 2 2

Example 1:Prisoners'dilemma By a case-by-case analysis, we found that both Prisoners would confess, Confess Silent regardless of what the other chooses. Embarrassingly,they could have both chosen“Silent"”to 4 5 serve less years. Confess 4 1 But people are selfish:They only care about their own payoff. 1 Resulting a dilemma:You 2 Silent pay two more years for 5 2 being selfish

Example 1: Prisoners’ dilemma ◼ By a case-by-case analysis, we found that both Prisoners would confess, regardless of what the other chooses. ◼ Embarrassingly, they could have both chosen “Silent” to serve less years. ◼ But people are selfish: They only care about their own payoff. ◼ Resulting a dilemma: You pay two more years for being selfish. Confess Silent Confess 4 4 5 1 Silent 1 5 2 2

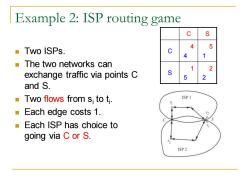
Example 2:ISP routing game C S 4 5 Two ISPs. C 4 1 a The two networks can 1 2 exchange traffic via points C S 5 2 and S. Two flows from s;to t. ISP 1 Each edge costs 1. 2 P Each ISP has choice to going via C or S. ISP 2

Example 2: ISP routing game ◼ Two ISPs. ◼ The two networks can exchange traffic via points C and S. ◼ Two flows from si to ti . ◼ Each edge costs 1. ◼ Each ISP has choice to going via C or S. C S C 4 4 5 1 S 1 5 2 2

Example 3:Pollution game N countries Each country faces the choice of either controlling pollution or not. Pollution control costs 3 for each country. Each country that pollutes adds 1 to the cost of all countries. What would you do if you are one of those countries? Suppose k countries don't control. For them:cost k For others:cost 3+k So all countries don't control!

Example 3: Pollution game ◼ N countries ◼ Each country faces the choice of either controlling pollution or not. ❑ Pollution control costs 3 for each country. ◼ Each country that pollutes adds 1 to the cost of all countries. ◼ What would you do if you are one of those countries? ◼ Suppose k countries don’t control. ❑ For them: cost = k ❑ For others: cost = 3+k ◼ So all countries don’t control!

Example 4:Battle of the sexes A boy and a girl want to decide whether to go to watch a baseball or a B S softball game. The boy prefers baseball 6 1 and the girl prefers softball. B 5 1 But they both like to spend the time together rather 2 5 than separately. S 2 6 What would you do?

Example 4: Battle of the sexes ◼ A boy and a girl want to decide whether to go to watch a baseball or a softball game. ◼ The boy prefers baseball and the girl prefers softball. ◼ But they both like to spend the time together rather than separately. ◼ What would you do? B S B 6 5 1 1 S 2 2 5 6

Formal definition In all previous games: There are a number of players Each has a set of strategies to choose from Each aims to maximize his/her payoff,or minimize his/her loss. Formally, ▣n-players. Each player i has a set Si of strategies. 0 LetS=Six…×Sn-A joint strategy is an s=s.sn- Each player i has a payoff function u(s)depending on a joint strategy s

Formal definition ◼ In all previous games: ❑ There are a number of players ❑ Each has a set of strategies to choose from ❑ Each aims to maximize his/her payoff, or minimize his/her loss. ◼ Formally, ❑ n-players. ❑ Each player i has a set Si of strategies. ❑ Let S = S1  ⋯  Sn . A joint strategy is an s = s1…sn . ❑ Each player i has a payoff function ui (s) depending on a joint strategy s