华南农业大学：《高等数学》课程电子教案（课件讲稿）第03章 微分中值定理与导数的应用 3.6 函数图形的描绘

在中学数学中，我们学过用“五点法”来画函数的图形。 但“五点法”有着固有的局限性，不能准确地画出函数的图形 在高等数学中，我们学会了利用函数的导数来确定函 数的单调区间和极值，点；学会了利用函数的二阶导数来 确定函数的凹凸区间及拐点. 知道了这些知识后，我们就能较准确地描绘出函数 的图形。 为了更准确地描绘函数的图形，我们再来学习一个 概念—渐近线，然后，再来研究函数图形描绘的基 本步骤和技巧！ 2009年7月3日星期五 目录 上页 返回

2009年7月3日星期五 1 目录 上页 下页 返回 在中学数学中，我们学过用“五点法”来画函数的图形。 但“五点法”有着固有的局限性，不能准确地画出函数的图形 在高等数学中，我们学会了利用函数的导数来确定函 数的单调区间和极值点；学会了利用函数的二阶导数来 确定函数的凹凸区间及拐点. 知道了这些知识后，我们就能较准确地描绘出函数 的图形。 为了更准确地描绘函数的图形，我们再来学习一个 概念 —— 渐近线， 然后，再来研究函数图形描绘的基 本步骤和技巧！

第三章 第六节 盖数图形的描拾 Plot of Functional Graph) 水平渐近线 一、曲线的渐进线〈 铅直渐近线 斜渐近线 二、函数图形的描绘 三、小结与思考练习 2009年7月3日星期五 2 目录 上页 、返回

2009年7月3日星期五 2 目录 上页 下页 返回 第六节 函数图形的描绘 第三章 （Plot of Functional Graph） 一、曲线的渐进线 水平渐近线 铅直渐近线 斜渐近线 二、函数图形的描绘 三、小结与思考练习

一、曲线的渐进线(Asymptote of Curve) 定义如果曲线上的一点沿着曲线趋于无穷远时，该 ,点与某条直线的距离趋于零，则称此直线为曲线的渐近 线 1.水平渐近线（平行于x轴的渐近线） 如果曲线y=f(x)的定义域是无限区间，且有 limf(x)=b或limf(x)=b X-00 则称直线y=b为曲线y=f(x)的水平渐近线。 例如，y=arctan x,有水平渐近线两条： 元 y= 2 2 2009年7月3日星期五 3 目录○ 上页 返回

2009年7月3日星期五 3 目录 上页 下页 返回 一、曲线的渐进线 定义 如果曲线上的一点沿着曲线趋于无穷远时，该 点与某条直线的距离趋于零，则称此直线为曲线的渐近 线． 1. 水平渐近线（平行于x 轴的渐近线） 如果曲线 y fx = ( ) 的定义域是无限区间，且有 lim ( ) x fx b →−∞ = 或 lim ( ) x fx b →+∞ = 则称直线 y b = 为曲线 y fx = ( ) 的水平渐近线。 例如， ,arctan （Asymptote of Curve) y = x 有水平渐近线两条: . 2 , 2 π −= π = yy

2.铅直渐近线（垂直于x轴的渐近线） 如果曲线y=f(x)有 lim f(x)=o lim f(x)=co, 则称直线x=c为曲线y=f(x)的铅直渐近线。 例如， 1 y= (x+2)(x-3)1 有铅直渐近线两条： X=-2,x=3. 2009年7月3日星期五 4 目录 上页)下页 。返回

2009年7月3日星期五 4 目录 上页 下页 返回 2. 铅直渐近线（垂直于x 轴的渐近线） 如果曲线 y fx = ( ) 有 lim ( ) x c f x → − = ∞ 或 lim ( ) x c f x → + = ∞ ， 则称直线 x = c 为曲线 y fx = ( ) 的铅直渐近线。 例如， 1 , ( 2)( 3) y x x = + − 有铅直渐近线两条: x = − x = .3,2

3.斜渐近线 如果曲线y=f(x)有 lim [f(x)-(ax+b)]=0 lim [f(x)-(ax+b)]=0(a0) +00 则称直线y=ax+b为曲线y=f(x)的斜渐近线。 下面来确定a,b. 回aa+n=0一▣/0-a+]-0 r→+0 X 将a代入lim[f(x)-(ax+b)]=0,得 X→十00 b=lim [f(x)-ax]. X→+00 2009年7月3日星期五 5 耳录 上页 下 返回

2009年7月3日星期五 5 目录 上页 下页 返回 3. 斜渐近线 如果曲线 y fx = ( ) 有 lim [ ( ) ( )] 0 x f x ax b →+∞ − += 或 lim [ ( ) ( )] 0 x f x ax b →−∞ − + = ( 0) a ≠ ， 则称直线 y ax b = + 为曲线 y fx = ( ) 的斜渐近线。 下面来确定a b, . lim [ ( ) ( )] 0 x f x ax b → +∞ − += ( im ) l 0 x fx b a x x x →+∞ − ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ + ( lim 0 ) x fx b a →+∞ x x − ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ + ( ) limx f x a →+∞ x = 将 a 代入 lim [ ( ) ( )] 0 x f x ax b →+∞ − + = ，得 lim [ ( ) ]. x b f x ax →+∞ = −

例1求曲线f)=2(x-2x+3) 的渐近线。 x-1 提示：(1)水平渐近线公式 (补充题) limf(x)=b或limf(x)=b x→-00 x→+00 (2)铅直渐近线公式 lim f(x)=o lim f(x)=co, x→C X->c (3)斜渐近线公式 a=lim f(x) b=lim [f(x)-ax]. x→+0 X→+00 (答案见下页) 2009年7月3日星期五 6 目录 上页( 返回

2009年7月3日星期五 6 目录 上页 下页 返回 例 1 求曲线 2( 2)( 3) ( ) 1 x x f x x− + = − 的渐近线． （补充题） 提示：（1）水平渐近线公式 lim ( ) x fx b →−∞ = 或 lim ( ) x fx b →+∞ = （2）铅直渐近线公式 lim ( ) x c f x → − = ∞ 或 lim ( ) x c f x → + = ∞ ， （3）斜渐近线公式 ( ) lim x f x a →+∞ x = lim [ ( ) ]. x b f x ax →+∞ = − （答案见下页）

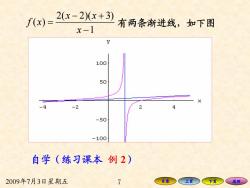
f0x)=2x-2)(x+3) 有两条渐进线，如下图 x-1 100 50 .a 2 -50 -100 自学（练习课本例2） 2009年7月3日星期五 7 目录○ 上页 下 、返回

2009年7月3日星期五 7 目录 上页 下页 返回 2( 2)( 3) ( ) 1 x x f x x− + = − 有两条渐进线，如下图 自学（练习课本 例 2）

二、函数图形的描绘 描绘函数的图形可按下列步骤： (1)确定函数的定义域； (2)确定函数的奇偶性、周期性； （3)确定函数的单调区间与极值，曲线的凹凸区间 与拐，点； （4)讨论曲线的渐近线； （5)由曲线方程计算曲线上一些，点的坐标，特别是 曲线和坐标轴的交点； (6)根据上述讨论，描绘函数f(x)的图形. 2009年7月3日星期五 8 目录 上页 、返回

2009年7月3日星期五 8 目录 上页 下页 返回 二、函数图形的描绘 描绘函数的图形可按下列步骤： （1）确定函数的定义域； （2）确定函数的奇偶性、周期性； （3）确定函数的单调区间与极值，曲线的凹凸区间 与拐点； （4）讨论曲线的渐近线； （5）由曲线方程计算曲线上一些点的坐标，特别是 曲线和坐标轴的交点； （6）根据上述讨论，描绘函数 f ( ) x 的图形．

x2 例2作出函数f(x)= 1e三的图形.（课本例3） V2π 解：(1)函数定义域为(-0，+o) (2)函数是偶函数，故函数图形关于y轴对称； (3)确定函数的单调区间与极值，曲线的凹凸区 间与拐，点； √2元 2 在[0，+o)上，当x=0时，f'(x)=0; 当x=1时，f"(x)=0 2009年7月3日星期五 0 日录 上页 返回

2009年7月3日星期五 9 目录 上页 下页 返回 例 2 作出函数 2 2 1 () e 2π x f x − = 的图形．（课本 例 3） 解：（1）函数定义域为(,) −∞ +∞ （2）函数是偶函数，故函数图形关于 y 轴对称； （3）确定函数的单调区间与极值，曲线的凹凸区 间与拐点； 2 2 1 () e , 2π x fx x − ′ = − 2 2 2 1 ( ) e ( 1) 2π x fx x − ′′ = − 在[0, ) +∞ 上，当 x = 0 时， f x ′() 0 = ； 当 x =1时， f x ′′() 0 =

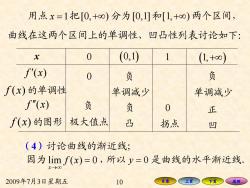
用点x=1把[0，+0)分为[0,1]和[1，+0)两个区间， 曲线在这两个区间上的单调性、凹凸性列表讨论如下： x 0 (0,1) 1 (1,+0) f'(x) 0 负 负 ∫(x)的单调性 单调减少 单调减少 f"(x) 负 负 0 正 f(x)的图形 极大值点 凸 拐点 凹 (4)讨论曲线的渐近线； 因为limf(x)=0,所以y=0是曲线的水平渐近线。 2009年7月3日星期五 10 目录 上页 返回

2009年7月3日星期五 10 目录 上页 下页 返回 曲线在这两个区间上的单调性、凹凸性列表讨论如下： 用点 x =1把[0, ) +∞ 分为[0,1]和[1, ) +∞ 两个区间， x f ′( ) x f ( ) x 的单调性 f ′′( ) x f ( ) x 的图形 0 0 负 (0,1) 极大值点 负 单调减少 负 凸 1 0 (1,+∞) 负 单调减少 正 拐点 凹 （4）讨论曲线的渐近线； 因为lim ( ) 0 x f x →∞ = ，所以 y = 0 是曲线的水平渐近线．