银川能源学院（银川大学）：《大学物理》课程教学资源（物理学PPT课件讲稿，大专）第六章 电磁感应（动生电动势）

§6-3动生电动势 第六章电磁感应 复习 1.产生感应电流的条件：穿过闭合回 路所围面积的磁通量发生变化 2.感应电动势的计算：法拉第电磁感应定律 dΦ WdΦ =-W 感应电流为I= dt R R dt 负号表方向，通常把大小和方向分开考虑。 3.用楞次定律判断感应电流的方向，感应电 动势的方向与它一致，是电势升高的方向，即从 低电势经内电路指向高电势。 上页 下页 返回 帮助

第六章 电磁感应 上页 下页 返回 帮助 §6-3 动生电动势 i d d Φ N t  = − 3. 用楞次定律判断感应电流的方向，感应电 动势的方向与它一致，是电势升高的方向，即从 低电势经内电路指向高电势。 复习 1. 产生感应电流的条件：穿过闭合回 路所围面积的磁通量发生变化 2. 感应电动势的计算：法拉第电磁感应定律 感应电流为 i d d i N Φ I R R t  = = − 负号表方向，通常把大小和方向分开考虑

§6-3动生电动势 第六章电磁感应 按照磁通量变化方式的不同，将感应电动势 分为两类： ①稳恒磁场中的导体运动，或者回路面积 变化等> 动生电动势 ②导体不动，磁场变化→ 感生电动势 上页 下页 返回 帮助

第六章 电磁感应 上页 下页 返回 帮助 §6-3 动生电动势 按照磁通量变化方式的不同 ，将感应电动势 分为两类： ①稳恒磁场中的导体运动 ，或者回路面积 变化等 动生电动势 ②导体不动，磁场变化 感生电动势

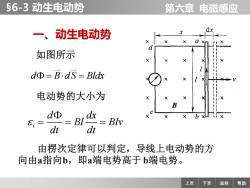
§6-3动生电动势 第六章电磁感应 一、 动生电动势 如图所示 dΦ=B·dS=Bldx 电动势的大小为 d=B dx 8= dt dt 由楞次定律可以判定，导线上电动势的方 向由a指向b,即a端电势高于b端电势。 上页 下页 返回 帮助

第六章 电磁感应 上页 下页 返回 帮助 §6-3 动生电动势 一、动生电动势 如图所示 d B dS Bldx  =  = i d dx Bl Blv dt dt   = = = 电动势的大小为 由楞次定律可以判定，导线上电动势的方 向由a指向b，即a端电势高于 b端电势

§6-3动生电动势 第六章电磁感应 动生电动势的非静电力来源 →洛伦兹力 F=(-e)i×B X × X 非静电场的场强： × × 片-E-0×B X e B 动生电动势： X c=Edi=∫(o×B)d 上页 下页 返回 帮助

第六章 电磁感应 上页 下页 返回 帮助 §6-3 动生电动势 B  v  b a 动生电动势的非静电力来源 洛伦兹力 F e B = −  ( )v k F E B e = =  − v i k d ( ) d b b a a  =  =   E l B l   v 非静电场的场强： 动生电动势：

§6-3动生电动势 第六章电磁感应 当任意形状的导线L在磁场中运动时 c=jE·d=(o×B)dl 1 动生电动势的方向除 X 了用楞次定律判定外，还 可以用上式来判断：电动 势的指向与非静电场场强 (v×B)在导线上分量的 方向相同。 如图所示 上页 下页 返回 帮助

第六章 电磁感应 上页 下页 返回 帮助 §6-3 动生电动势 当任意形状的导线L在磁场中运动时 i k d ( ) d L L  =  =   E l B l   v 动生电动势的方向除 了用楞次定律判定外，还 可以用上式来判断：电动 势的指向与非静电场场强 （ ）在导线上分量的 方向相同。 v B 如图所示

§6-3动生电动势 第六章电磁感应 动生电动势 N 同左运动 问石运动 上页 下页 返回 帮助

第六章 电磁感应 上页 下页 返回 帮助 §6-3 动生电动势 动生电动势

§6-3动生电动势 第六章电磁感应 发电机原理 上页 下页 返回 帮助

第六章 电磁感应 上页 下页 返回 帮助 §6-3 动生电动势 发电机原理

§6-3动生电动势 第六章电磁感应 二、动生电动势的计算 两种方法：一种是根据法拉第电磁感应定律 来计算； 另一种是利用￡=∫（⑦×B)d来计算。 下面通过例题说明后一种方法的运用。 例6-2一长为L的铜棒在磁感应强度为五 的匀 强磁场中，以角速度)在与磁场方向垂直的平面上绕 棒的一端O转动，求棒中的感应电动势。 上页 下页 返回 帮助

第六章 电磁感应 上页 下页 返回 帮助 §6-3 动生电动势 二、动生电动势的计算 两种方法：一种是根据法拉第电磁感应定律 来计算； 另一种是利用  i =   L ( ) d v B l 来计算。 下面通过例题说明后一种方法的运用。 例6-2 一长为 的铜棒在磁感应强度为 的匀 强磁场中,以角速度 在与磁场方向垂直的平面上绕 棒的一端O转动，求棒中的感应电动势。  L B 

§6-3动生电动势 第六章电磁感应 已知：L,B,) 求： 解：由￡=∫（⑦×B)d得 E=∫6 vBdl -olBdI-mB BoL 2 动生电动势的方向由O指向P,或者说Vp>V。 上页 下页 返回 帮助

第六章 电磁感应 上页 下页 返回 帮助 §6-3 动生电动势 已知： L, B,  求： i  + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + o  P B   v  l  d 解:由 2 0 0 1 d 2 L L = =   lB l B l  i 0 L  = Bdl  v 1 2 2 = B L  动生电动势的方向由O指向P，或者说 VP VO i ( ) d L  =   B l  v 得

§6-3动生电动势 第六章电磁感应 例6-3如图所示，在通有电流工的直导线旁有一金属棒 b,金属棒与直导线共面，且互相垂直。金属棒以匀速y平行 于长直导线运动。求金属棒中的感应电动势。 已知：I,yra,b 求： b 解： B= 41 2 e,=∫(×B)d7 ∴e=gdr=-签n 由于6，<0，所以电动势的方向由b指向a，即a端电势较高。 上页 下页 返回 帮助

第六章 电磁感应 上页 下页 返回 帮助 §6-3 动生电动势 例6-3 如图所示,在通有电流 I 的直导线旁有一金属棒 ab，金属棒与直导线共面，且互相垂直。金属棒以匀速 平行 于长直导线运动。求金属棒中的感应电动势。 v ( ) d b i a  =    v B l 0 0 2π 2π d ln b b a a r Iv Iv r i r r r r    = − = −   由于  i  0 ,所以电动势的方向由b 指向a , 即a 端电势较高。 b I a v  a r r d r b r 求： i  已知： I, , , v a r b r 解: 0 2π I B r  =