西安电子科技大学：《电磁场与电磁波》课程电子教案（PPT课件讲稿）第2章 静电场

第2章静电场 黄丘林 电子工程学院 西安电子科技大学

第2章 静电场 黄丘林 电子工程学院 西安电子科技大学 1

本章提纲 。1库仑定律和电场强度 。2真空中的高斯定理 。3电位 。4介质极化与高斯定理的一般形式 。5静电场的基本方程和边界条件 。6电容 。7静电场的能量 2

本章提纲  1 库仑定律和电场强度  2 真空中的高斯定理  3 电位  4 介质极化与高斯定理的一般形式  5 静电场的基本方程和边界条件  6 电容  7 静电场的能量 2

。所谓静电场是指相对于观察者而言静止的电荷所产生 的场。 0) 对静电场的系统性、科学性的研究则是在1785年法国 科学家库仑（Chavles Augustin Coulomb, 1736~1806)发现了以其名字命名的“库仑定律” 库仑定律和迭加原理一起，构成了静电场的理论基础。 。本章从库仑定律和迭加原理出发，得出描述真空中静 电场的基本方程，进而讨论介质中的静电场，静电场 的基本解法以及静电场的能量。 3

 所谓静电场是指相对于观察者而言静止的电荷所产生 的场。  对静电场的系统性、科学性的研究则是在1785年法国 科学家库仑（Chavles Augustin Coulomb， 1736～1806）发现了以其名字命名的“库仑定律”。 库仑定律和迭加原理一起，构成了静电场的理论基础。  本章从库仑定律和迭加原理出发，得出描述真空中静 电场的基本方程，进而讨论介质中的静电场，静电场 的基本解法以及静电场的能量。 3

1库仑定律和电场强度 。库仑定律 ·库仑定律是一条实验定律，是在大量实验结果的基 础上，总结抽象出的描述真空中两个静止的点电荷 间相互作用力的定律。 点电荷：是指带电体的尺寸远小于彼此间的距离， 而认为电荷集中于一点的一种理想化模型。 ·库仑定律可用矢量式表示为： qq'ax 4π6R2

1 库仑定律和电场强度 库仑定律  库仑定律是一条实验定律，是在大量实验结果的基 础上，总结抽象出的描述真空中两个静止的点电荷 间相互作用力的定律。  点电荷：是指带电体的尺寸远小于彼此间的距离， 而认为电荷集中于一点的一种理想化模型。  库仑定律可用矢量式表示为： 2 0 4 R q q a F R q     = 4

1库仑定律和电场强度 。9、9一两个点电荷的电量。单位库仑(C〉 ·R一两个点电荷间的距离。单位米(m) a一从指向的单位矢量。 ● 6一真空中的介电常数。6。= ,1xI0法拉/米(F/m) 36元 瓦，一9所受到的作用力。 9、9的位置可用它们所在点的矢径表示，则 F,()= 9q(-F 4π。产-F3 5

1 库仑定律和电场强度  、 —两个点电荷的电量。单位库仑（C）  R—两个点电荷间的距离。单位米（m）  —从 指向 的单位矢量。  —真空中的介电常数。 法拉/米（F/m）  — 所受到的作用力。 、 的位置可用它们所在点的矢径表示，则 q q  R a  0  9 0 10 36 1 − =    Fq q 3 4 0 ( ) ( ) r r q q r r F r q −   −  =        q q  5

1库仑定律和电场强度 。迭加原理 当真空中存在两个以上的点电荷时，实验表明，任 何两个点电荷间的作用力不受其它点电荷的影响， 所以点电荷g所受的力是其它所有点电荷对它的作 用力的矢量和，即满足迭加性。 F,()）=F+F2++则=2 9〉二 下-列 其中F①表示处的点电荷9：对q的作用力。 6

1 库仑定律和电场强度 迭加原理  当真空中存在两个以上的点电荷时，实验表明，任 何两个点电荷间的作用力不受其它点电荷的影响， 所以点电荷q所受的力是其它所有点电荷对它的作 用力的矢量和，即满足迭加性。 其中 表示 处的点电荷 对q的作用力。 = −  −  = + + + = n i i n i i q q q q r r q q r r F r F F F 0 1 (1) (2) ( ) ( ) 4 ( )           (i) Fq ir  i q 6

1库仑定律和电场强度 例有三个点电荷电量分别为9，=92=106C,4=-102C, 它们处于一个边长为1m的等边三角形的顶点上，求9所 受的力。 解：由图知下= 2 -a,=-a, 93 92 下-月= F-引=1 f-g=空a-4F-到-l 7

例 有三个点电荷电量分别为 C， C， 它们处于一个边长为1m的等边三角形的顶点上，求 所 受的力。 1 库仑定律和电场强度 6 1 2 10− q = q = 12 3 10− q = − q3 7

1库仑定律和电场强度 由叠加原理得： 93 9,G-9,厅-) 46F-F- 9j小会] =-9√5×10°a,(牛顿) 8

1 库仑定律和电场强度 由叠加原理得： 8

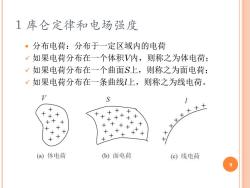
1库仑定律和电场强度 。分布电荷：分布于一定区域内的电荷 V 如果电荷分布在一个体积V内，则称之为体电荷： V1 如果电荷分布在一个曲面S上，则称之为面电荷： √如果电荷分布在一条曲线上，则称之为线电荷。 S + × + ×× + + + + 大大×××火+土 (a)体电荷 (b)面电荷 (c)线电荷 9

1 库仑定律和电场强度  分布电荷：分布于一定区域内的电荷 ✓ 如果电荷分布在一个体积V内，则称之为体电荷； ✓ 如果电荷分布在一个曲面S上，则称之为面电荷； ✓ 如果电荷分布在一条曲线l上，则称之为线电荷。 9

1库仑定律和电场强度 为了定量地描述电荷在区域内分布的疏密程度，引入 电荷密度的概念。 ·对于体电荷，在电荷分布在区域V内下处取体积元△V,， 若其中电荷的电量为△q,则定义： 体电荷密度：p(r)=lim △g=dg A-→0△VdW (C/m3)） ·类似地，可定义面电荷密度和线电荷密度分别为： p,(F)=lim △5→0 △s d函 (C/m2) p,()lim △9= dq (C/m〉 △1-→0 dl 10

1 库仑定律和电场强度 为了定量地描述电荷在区域内分布的疏密程度，引入 电荷密度的概念。  对于体电荷，在电荷分布在区域V内 处取体积元 ， 若其中电荷的电量为 ，则定义：  类似地，可定义面电荷密度和线电荷密度分别为： （C/m²） （C/m） r  V q dV dq V q r V =   =  →0 ( ) lim   ( ) ds dq s q r s s =   =  →0 lim   ( ) dl dq l q r l l =   =  →0 lim   体电荷密度： （C/m³） 10