中国人民大学：《金融计量学》课程教学资源（PPT课件）Lecture 04 平稳金融时间序列——AR模型 4.1 基本概念 4.2 一阶自回归模型 AR（1）

第四章平稳金融时间序列：AR模型 4.1 基本概念 4.2一阶自回归模型AR(1) 4.3二阶自回归模型AR（2) 4.4 p阶自回归模型AR（p)

2 第四章 平稳金融时间序列：AR模型 4.1 基本概念 4.2 一阶自回归模型 AR（1） 4.3 二阶自回归模型 AR（2） 4.4 p阶自回归模型 AR（p）

4.1 基本概念 4.1.1随机过程与数据生成过程 随机过程： 从随机概率论的概念出发，随机过 程是一系列或一组随机变量的集合，用 来描绘随机现象在接连不断地观测过程 中的实现结果。对于每一次观测，得到 一个观测到的随机变量

4.1 基本概念 4.1.1 随机过程与数据生成过程 随机过程： 从随机概率论的概念出发，随机过 程是一系列或一组随机变量的集合，用 来描绘随机现象在接连不断地观测过程 中的实现结果。对于每一次观测，得到 一个观测到的随机变量

如果使用数学语言来定义随机函 数，给定一个时间域T,对于T中每一 个参数t,都有一个取值于确定集合W 的随机变量ys),其中s属于一个特定 的样本区间。所以对于一个给定的t, Y(s)是一个随机变量。对于一个确定的 样本s,Y(S)就是在s上的一组实现值，而 集合Y(S),t∈T}就是一个随机过程

如果使用数学语言来定义随机函 数，给定一个时间域T，对于T中每一 个参数t，都有一个取值于确定集合W 的随机变量 ，其中s属于一个特定 的样本区间。所以对于一个给定的t， 是一个随机变量。对于一个确定的 样本s， 就是在s上的一组实现值,而 集合 就是一个随机过程。 ( ) t Y s ( ) t Y s ( ) t Y s { ( ), } t Y s t T 

数据生成过程： 利用下面的回归模型来说明，即： y=Bx,+e,,:ii.d.(0,o0),t=1,2,L,T 假设模型中所有系数已知或者是已 经设立了的，那么给定解释变量x的一 组观测值，回归模型就可以生成对应的 一组y,值，则模型就是一个数据生成过 程

数据生成过程: 利用下面的回归模型来说明，即： 假设模型中所有系数已知或者是已 经设立了的，那么给定解释变量 的一 组观测值，回归模型就可以生成对应的 一组 值，则模型就是一个数据生成过 程。 2 0 0 , . . .(0, ), 1,2, , t t t t y x i i d t T = + =     : Lt x t y

DGP适用于理论上的问题与真实世 界的事例之间的比较。 例如：中国国际股票指数和随机游走 过程看上去相似吗？股票的收益率序列 符合白噪音过程吗？

DGP适用于理论上的问题与真实世 界的事例之间的比较。 例如:中国国际股票指数和随机游走 过程看上去相似吗？股票的收益率序列 符合白噪音过程吗？

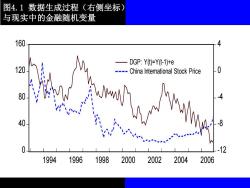
图4.1数据生成过程（右侧坐标） 与现实中的金融随机变量 160 DGP:Y(t)=Y(t-1)+e 120 ----China International Stock Price .0 80 A 40 8 12 1994 1996 1998 2000 2002 2004 2006

图4.1 数据生成过程（右侧坐标） 与现实中的金融随机变量 0 40 80 120 160 -12 -8 -4 0 4 1994 1996 1998 2000 2002 2004 2006 DGP: Y(t)=Y(t-1)+e China International Stock Price

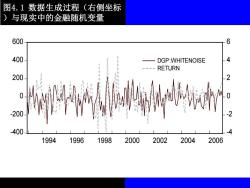
图4.1数据生成过程（右侧坐标 )与现实中的金融随机变量 600 6 400 DGP:WHITENOISE ----RETURN 200 2 祥喻 200 400 1994 1996 1998 2000 2002 2004 2006

图4.1 数据生成过程（右侧坐标 ）与现实中的金融随机变量 -400 -200 0 200 400 600 -4 -2 0 2 4 6 1994 1996 1998 2000 2002 2004 2006 DGP:WHITENOISE RETURN

4.1.2自协方差与自相关函数 假定y是一个随机变量，自协方差 定义的是y,与其自身滞后期之间的协方 差，即“自身的协方差”。常见的协方 差的基本定义是： Cov(X,Y)=E[X-E(X)][Y-E(Y)] 其中：E[]表示期望。从而可以知道，y 与其自身滞后j期y,之间的协方差定义 为：y,=[y-E(0-E0】小j=0,山，+2，L

4.1.2 自协方差与自相关函数 假定 是一个随机变量，自协方差 定义的是 与其自身滞后期之间的协方 差，即“自身的协方差”。常见的协方 差的基本定义是： 其中： 表示期望。从而可以知道， 与其自身滞后j期 之间的协方差定义 为： t y t y Cov X Y E X E X Y E Y ( , ) ( ) ( ) = − −    E[ ] t y t j y −  j t t t - j t - j = − − =   E y E y y E y j  ( ) ( ) , 0, 1, 2,     L

对于均值保持不变的随机过程来说， y,=E[y-4][yy-4,j=0,1,2,L j=0时，即为方差： o=ar(y,)=E[y-4][yw-4]

对于均值保持不变的随机过程来说， 时，即为方差：   , 0, 1, 2,    j t t - j = − − =   E y y j     L    0 = = − − Var y E y y ( )t t t-0    j = 0

随机变量x和y的相关系数模型为： Cov(x,y) P=ar(x)Var(y） 自相关函数，即y,与y的自相关 函数定义为： Cov(y,yj) DVa(y.)War( =,j=0,+1,+2,L 一般将P相对于滞后期数j绘制出的 图示称为自相关图

随机变量x和y的相关系数模型为： 自相关函数，即 与 的自相关 函数定义为： 一般将 相对于滞后期数j绘制出的 图示称为自相关图。 ( , ) ( ) ( ) Cov x y Var x Var y  = t y t - j y ( , ) , 0, 1, 2, ( ) ( ) t t - j j t t - j Cov y y j Var y Var y  = =   L  j