《数学模型与数学实验》课程书籍文献（数学建模算法大全）第15章 常微分方程的解法

第十五章常微分方程的解法 建立微分方程只是解决问题的第一步，通常需要求出方程的解来说明实际现象，并 加以检验。如果能得到解析形式的解固然是便于分析和应用的，但是我们知道，只有线 性常系数微分方程，并且自由项是某些特殊类型的函数时，才可以肯定得到这样的解 而绝大多数变系数方程、非线性方程都是所谓“解不出来”的，即使看起来非常简单的 方程如密-户+，于是对于用微分方程解决实际月恩来说，数值解法就是一个十 分重要的手段。 盘=x) a≤x≤b 1) ya)=% 在下面的讨论中，我们总假定函数f(x,y)连续，且关于y满足李普希兹Lipschitz)条 件，即存在常激L,使得 lf(x,y)-f(x,)Lly- 这样，由常微分方程理论知，初值问题(1)的解必定存在唯一。 所谓数值解法，就是求问题(1)的解y(x)在若干点 a=x<<<<X=b 处的近似值y(n=1,2,.,N)的方法，yn(n=1,2,.,N)称为问题(1)的数值解， 首先要将微分方程离散化，一般采用以下几种方法： 若用向前差商)-代特y(x,)代入()中的微分方程，则料 h -fxx,》a=0,1 h 化简得 x)≈x)+hf(x,x》 如果用y(x)的近似值y代入上式右端，所得结果作为(x)的近似值，记为y+1, 则有 yn+hf(xyn)(n=0,l.） 这样，问题(1)的近似解可通过求解下述问题 v=y+hf(xy.)(n=0.I.) (3) %=a) 得到，按式(3)由初值可逐次算出，2，.。式(3)是个离散化的问题，称为差 分方程初值问题

-179- 第十五章 常微分方程的解法 建立微分方程只是解决问题的第一步，通常需要求出方程的解来说明实际现象，并 加以检验。如果能得到解析形式的解固然是便于分析和应用的，但是我们知道，只有线 性常系数微分方程，并且自由项是某些特殊类型的函数时，才可以肯定得到这样的解， 而绝大多数变系数方程、非线性方程都是所谓“解不出来”的，即使看起来非常简单的 方程如 2 2 y x dx dy = + ，于是对于用微分方程解决实际问题来说，数值解法就是一个十 分重要的手段。 §1 常微分方程的离散化 下面主要讨论一阶常微分方程的初值问题，其一般形式是 ⎪ ⎩ ⎪ ⎨ ⎧ = = ≤ ≤ 0 ( ) ( , ) y a y f x y a x b dx dy (1) 在下面的讨论中，我们总假定函数 f (x, y) 连续，且关于 y 满足李普希兹(Lipschitz)条 件，即存在常数 L ，使得 | f (x, y) − f (x, y) |≤ L | y − y | 这样，由常微分方程理论知，初值问题(1)的解必定存在唯一。 所谓数值解法，就是求问题（1）的解 y(x) 在若干点 a = x0 < x1 < x2 <L< xN = b 处的近似值 y (n 1,2, ,N) n = L 的方法， y (n 1,2, ,N) n = L 称为问题（1）的数值解， n n n h = x − x +1 称为由 n x 到 n+1 x 的步长。今后如无特别说明，我们总取步长为常量h 。 建立数值解法，首先要将微分方程离散化，一般采用以下几种方法： （i）用差商近似导数 若用向前差商 h y x y x n n ( ) ( ) +1 − 代替 '( ) n y x 代入（1）中的微分方程，则得 ( , ( )) ( 0,1, ) ( ) ( ) 1 ≈ = L + − f x y x n h y x y x n n n n 化简得 ( ) ( ) ( , ( )) n 1 n n n y x ≈ y x + hf x y x + 如果用 ( ) n y x 的近似值 n y 代入上式右端，所得结果作为 ( ) n+1 y x 的近似值，记为 n+1 y ， 则有 ( , ) ( 0,1, ) yn+1 = yn + hf xn yn n = L （2） 这样，问题（1）的近似解可通过求解下述问题 ⎩ ⎨ ⎧ = + = + = ( ) ( , ) ( 0,1, ) 0 1 y y a y y hf x y n n n n n L （3） 得到，按式（3）由初值 0 y 可逐次算出 y1, y2 ,L。式（3）是个离散化的问题，称为差 分方程初值问题

需要说明的是，用不同的差商近似导数，将得到不同的计算公式。 铜器的解表积分形式，用数值积分方法离散化。如，对微分方程两瑞 且 积分，得 y(x)-xn)=f(x,(x)k(n=0,1 (4) 右边的积分用矩形公式或梯形公式计算。 (ii)Taylor多项式近似 将函数(x)在xn处展开，取一次Taylor多项式近似，则得 y(xm1)≈(xn)+hy(x)=yxn)+hf(xn,xn)》 再将y(x)的近似值y,代入上式右端，所得结果作为(x)的近似值y1,得到离 散化的计算公式 y=y+hf(x:y) 以上三种方法都是将微分方程离散化的常用方法，每一类方法又可导出不同形式的 计算公式。其中的Taylor展开法，不仅可以得到求数值解的公式，而且容易估计截断 误差。 Euler 方法就是用差分方程初值问题(3)的解来近似微分方程初值问题(1)的解 即由公式(3)依次算出x,)的近似值y(=12,).这组公式求问题(1)的数值 解称为向前Euler公式。 如果在微分方程离散化时，用向后差商代替导数，即y化)~儿)-】 则得计算公式 =y.+h(x)(n=0.1) (5) %=y(a) 用这组公式求问题(I)的数值解称为向后Euler公式。 向后Euler法与Euler法形式上相似，但实际计算时却复杂得多。向前Euler公式 是显式的，可直接求解。向后Er公式的右端含有1，因此是隐式公式，一般要用 迭代法求解，迭代公式通常为 [y =y.+hf(x.y.) (6) y=y+hf()(k=0.1.2.) 22 Euler方法的误差估计 对于向前Euler公式(3)我们看到，当n=1,2,.时公式右瑞的y,都是近似的， 所以用它计算的y,会有累积误差，分析累积误差比较复杂，这里先讨论比较简单的 所谓局部截断误差。 假定用(3)式时右端的y没有误差，即y。=y(x.),那么由此算出 yn1=x)+hf(x,Jxn》 (7) -180-

-180- 需要说明的是，用不同的差商近似导数，将得到不同的计算公式。 （ii）用数值积分方法 将问题（1）的解表成积分形式，用数值积分方法离散化。例如，对微分方程两端 积分，得 ∫ + + − = = 1 ( ) ( ) ( , ( )) ( 0,1, ) 1 n n x x y xn y xn f x y x dx n L (4) 右边的积分用矩形公式或梯形公式计算。 （iii）Taylor 多项式近似 将函数 y(x) 在 n x 处展开，取一次 Taylor 多项式近似，则得 ( ) ( ) '( ) ( ) ( , ( )) n 1 n n n n n y x ≈ y x + hy x = y x + hf x y x + 再将 ( ) n y x 的近似值 n y 代入上式右端，所得结果作为 ( ) n+1 y x 的近似值 n+1 y ，得到离 散化的计算公式 ( , ) n 1 n n n y = y + hf x y + 以上三种方法都是将微分方程离散化的常用方法，每一类方法又可导出不同形式的 计算公式。其中的 Taylor 展开法，不仅可以得到求数值解的公式，而且容易估计截断 误差。 §2 欧拉（Euler）方法 2.1 Euler 方法 Euler 方法就是用差分方程初值问题（3）的解来近似微分方程初值问题（1）的解， 即由公式（3）依次算出 ( ) n y x 的近似值 y (n = 1,2,L) n 。这组公式求问题（1）的数值 解称为向前 Euler 公式。 如果在微分方程离散化时，用向后差商代替导数，即 h y x y x y x n n n ( ) ( ) '( ) 1 1 − ≈ + + ， 则得计算公式 ⎩ ⎨ ⎧ = + = + + + = ( ) ( , ) ( 0,1, ) 0 1 1 1 y y a y y hf x y n n n n n L （5） 用这组公式求问题（1）的数值解称为向后 Euler 公式。 向后 Euler 法与 Euler 法形式上相似，但实际计算时却复杂得多。向前 Euler 公式 是显式的，可直接求解。向后 Euler 公式的右端含有 n+1 y ，因此是隐式公式，一般要用 迭代法求解，迭代公式通常为 ⎪⎩ ⎪ ⎨ ⎧ = + = = + + + + + + ( , ) ( 0,1,2, ) ( , ) ( ) 1 1 ( 1) 1 (0) 1 y y hf x y k L y y hf x y k n n n k n n n n n （6） 2.2 Euler 方法的误差估计 对于向前 Euler 公式（3）我们看到，当n = 1,2,L时公式右端的 n y 都是近似的， 所以用它计算的 n+1 y 会有累积误差，分析累积误差比较复杂，这里先讨论比较简单的 所谓局部截断误差。 假定用（3）式时右端的 n y 没有误差，即 ( ) n n y = y x ，那么由此算出 ( ) ( , ( )) n 1 n n n y = y x + hf x y x + （7）

局部截断误差指的是，按(7)式计算由xn到x1这一步的计算值1与精确值(xa+) 之差(xn+1）-y1。为了估计它，由Taylor展开得到的精确值xi)是 ，y"(x)+0h) (8) (7)、(8)两式相减（注意到y=f(x,)得 -经yx,)+ow)=0) (9) 即局部截断误差是？阶的，而数值算法的精度定义为： 若一种算法的局部截断误差为O(hP),则称该算法具有p阶精度。 显然p越大，方法的精度越高。式(9)说明，向前Euler方法是一阶方法，因此 它的精度不高。 s3改进的Euler方法 利用数积分方法将微分方程离散化时若用梯形公式计算式中之右端积分、 即 fx,x》kfx,x,》+fxx川 并用yn,y1代替y(xbxi),则得计算公式 1=y.+3/xy,)+fxi】 这是求解初值问题①的梯形公式 林形公式起式格公 公工 格形公式为功方法 比矩 yo=y+hf(xn.y) yf)+f. (10 (k=01,2,. 由于函数f(x,y)关于y满足Lipschit条件，容易看出 1-竖-片 其中L为常数。因此，当0<化<1时，法代收敛。但这样做计算量较大 如果实际计算时精度要求不太高，用公式(10)求解时，每步可以只迭代一次，由此导 出一 新的 攻进Euler法 按式(5)计算问题(1)的数值解时，如果每步只迭代一次，相当于将Eulr公式 与梯形公式结合使用：先用Euler公式求y的一个初步近似值元1，称为预测值，然 后用梯形公式校正求得近似值y1,即 -181

-181- 局部截断误差指的是，按（7）式计算由 n x 到 n+1 x 这一步的计算值 n+1 y 与精确值 ( ) n+1 y x 之差 1 1 ( ) n+ − n+ y x y 。为了估计它，由 Taylor 展开得到的精确值 ( ) n+1 y x 是 ' '( ) ( ) 2 ( ) ( ) '( ) 3 2 1 y x O h h y x y x hy x n+ = n + n + n + （8） （7）、（8）两式相减（注意到 y'= f (x, y) ）得 ' '( ) ( ) ( ) 2 ( ) 3 2 2 1 1 y x O h O h h y x y n+ − n+ = n + ≈ （9） 即局部截断误差是 2 h 阶的，而数值算法的精度定义为： 若一种算法的局部截断误差为 ( ) p+1 O h ，则称该算法具有 p 阶精度。 显然 p 越大，方法的精度越高。式（9）说明，向前 Euler 方法是一阶方法，因此 它的精度不高。 §3 改进的 Euler 方法 3.1 梯形公式 利用数值积分方法将微分方程离散化时，若用梯形公式计算式(4)中之右端积分， 即 [ ( , ( )) ( , ( ))] 2 ( , ( )) 1 1 1 ∫ ≈ + + + + n n n n x x f x y x f x y x h f x y x dx n n 并用 1 , n n+ y y 代替 ( ), ( ) n n+1 y x y x ，则得计算公式 [ ( , ) ( , )] 2 n+1 = n + n n + n+1 n+1 f x y f x y h y y 这就是求解初值问题（1）的梯形公式。 直观上容易看出，用梯形公式计算数值积分要比矩形公式好。梯形公式为二阶方法。 梯形公式也是隐式格式，一般需用迭代法求解，迭代公式为 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = = + + = + + + + + + ( 0,1,2, ) [ ( , ) ( , )] 2 ( , ) ( ) 1 1 ( 1) 1 (0) 1 k L f x y f x y h y y y y hf x y k n n n n n k n n n n n (10) 由于函数 f (x, y) 关于 y 满足 Lipschitz 条件，容易看出 | | 2 | | ( 1) 1 ( ) 1 ( ) 1 ( 1) 1 − + + + + + − ≤ − k n k n k n k n y y hL y y 其中 L 为 Lipschitz 常数。因此，当 1 2 0 < < hL 时，迭代收敛。但这样做计算量较大。 如果实际计算时精度要求不太高，用公式（10）求解时，每步可以只迭代一次，由此导 出一种新的方法—改进 Euler 法。 3.2 改进 Euler 法 按式（5）计算问题（1）的数值解时，如果每步只迭代一次，相当于将 Euler 公式 与梯形公式结合使用：先用 Euler 公式求 n+1 y 的一个初步近似值 n+1 y ，称为预测值，然 后用梯形公式校正求得近似值 n+1 y ，即

t=y+hf(x.y) 年 y1=n+2[fxny,)+fx1,i)】校正 (11) 式(II)称为由Euler公式和梯形公式得到的预测一校正系统，也叫改进Euler法。 为便于编制程序上机，式(11)常改写成 yp=y+hf(x,y.) yo=y+hf(x+h,y) (12) =0,+y,) 改进Euler法是二阶方法。 应有 x-=yx,+m).0<0<1 注意到方程y=(x,y)就有 yx)=y(x )+hf(x +hy(x+)) (13) 不妨记下=f(x。+m,(x。+),称为区间[x,x]上的平均斜率。可见给出一种 斜率下，(13)式就对应地导出一种算法。 向前Euler公式简单地取f(x,y)为,精度自然很低。改进的Euler公式可理 解为F取f(xn,y),f(x1,）的平均值，其中1=y+hf(xn,yn),这种处 理提高了精度 如上分析启示我们，在区间[x,x+]内多取几个点，将它们的斜率加权平均作为 下，就有可能构造出精度更高的计算公式。这就是龙格一库塔方法的基本思想。 4.1 首先不妨在区间[x,x内仍取2个点，仿照(13)式用以下形式试一下 y1=y.+h(元k+k) k1=1（x.,V) (14) k2 =f(x +ah.y+Bhk )0<a.B<1 其中元，入，a,B为待定系数，看看如何确定它们使(14)式的精度尽量高。为此我们 分析局部截断误差(x)一y1,因为y.=(x),所以(14)可以化为 -182

-182- ⎪ ⎩ ⎪ ⎨ ⎧ = + + = + + + + + 校正 预测 [ ( , ) ( , ) ] 2 ( , ) 1 1 1 1 n n n n n n n n n n f x y f x y h y y y y hf x y （11） 式（11）称为由 Euler 公式和梯形公式得到的预测—校正系统，也叫改进 Euler 法。 为便于编制程序上机，式（11）常改写成 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = + = + + = + + ( ) 2 1 ( , ) ( , ) n 1 p q q n n p p n n n y y y y y hf x h y y y hf x y （12） 改进 Euler 法是二阶方法。 §4 龙格—库塔（Runge—Kutta）方法 回到 Euler 方法的基本思想—用差商代替导数—上来。实际上，按照微分中值定理 应有 '( ), 0 1 ( ) ( ) 1 = + < < + − y x θh θ h y x y x n n n 注意到方程 y'= f (x, y) 就有 ( ) ( ) ( , ( )) y xn+1 = y xn + hf xn +θh y xn +θh （13） 不妨记 K f (x h, y(x h)) = n +θ n +θ ，称为区间[ , ] n n+1 x x 上的平均斜率。可见给出一种 斜率 K ，（13）式就对应地导出一种算法。 向前 Euler 公式简单地取 ( , ) n n f x y 为 K ，精度自然很低。改进的 Euler 公式可理 解为 K 取 ( , ) n n f x y ， ( , ) n+1 n+1 f x y 的平均值，其中 ( , ) n 1 n n n y = y + hf x y + ，这种处 理提高了精度。 如上分析启示我们，在区间[ , ] n n+1 x x 内多取几个点，将它们的斜率加权平均作为 K ，就有可能构造出精度更高的计算公式。这就是龙格—库塔方法的基本思想。 4.1 首先不妨在区间[ , ] n n+1 x x 内仍取 2 个点，仿照（13）式用以下形式试一下 ⎪ ⎩ ⎪ ⎨ ⎧ = + + < < = + = + + ( , ), 0 , 1 ( , ) ( ) 2 1 1 1 1 1 2 2 α β α β λ λ k f x h y hk k f x y y y h k k n n n n n n （14） 其中 λ1,λ2 ,α,β 为待定系数，看看如何确定它们使（14）式的精度尽量高。为此我们 分析局部截断误差 1 1 ( ) n+ − n+ y x y ，因为 ( ) n n y = y x ，所以（14）可以化为

yn1=(xn)+h2k1+2k3） k=f(xv(x))=y'(x) k2 =f(x +ah.y(x)+Bhk) (15 =f(xn,y(xn)》+cf(xn,xn》 +kf,(xn,y(xn)》+Oh2) 其中k2在点(xn,yx.)》作了Taylor展开。(15)式又可表为 y=,)+(+2hyx,)+h'U+E )+06 注意到 )=,)+.)+ 2y")+0h) 中y=∫，y"=了+，可见为使误差x)-y1=O(),只须令 +名=1，a=分是1 (16) 待定系数满足(16)的(15)式称为2阶龙格一库塔公式。由于(16)式有4个未知数 而只有3个方程，所以解不唯一。不难发现，若令名=名=支，口=B=1,即为政 进的Euler公式。可以证明，在[x,x内只取2点的龙格一库塔公式精度最高为2 阶 库塔公式 ya=y+h(k+hk2+aks+Aks) k=f(.) k2 =f(x +a h,y+B hk (17) k3 =f(x +ah.y+Bhk +B hk2) k=f(x +ash,y +Bhk +B hk,+B hks) 其中待定系数，,B共13个，经过与推导2阶龙格一库塔公式类似、但更复杂的计 算，得到使局部误差y(x)-y1=O(h)的11个方程。取既满足这些方程、又较简 单的一组元，a,B,可得 -183-

-183- ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ + + = + = + + = = + = + + ( , ( )) ( ) ( , ( )) ( , ( )) ( , ( ) ) ( , ( )) '( ) ( ) ( ) 2 1 2 1 1 1 1 1 2 2 hk f x y x O h f x y x hf x y x k f x h y x hk k f x y x y x y y x h k k y n n n n x n n n n n n n n n β α α β λ λ （15） 其中 2 k 在点( , ( )) n n x y x 作了 Taylor 展开。（15）式又可表为 ( ) ( ) '( ) ( ) ( ) 2 3 yn+1 = y xn + 1 + 2 hy xn + 2 h f x + ff y +O h α β λ λ λ α 注意到 ' '( ) ( ) 2 ( ) ( ) '( ) 3 2 1 y x O h h y x y x hy x n+ = n + n + n + 中 y'= f ， x y y' '= f + ff ，可见为使误差 ( ) ( ) 3 y xn+1 − yn+1 = O h ，只须令 1 λ1 + λ2 = ， 2 1 λ2α = ， =1 α β （16） 待定系数满足（16）的（15）式称为 2 阶龙格—库塔公式。由于（16）式有 4 个未知数 而只有 3 个方程，所以解不唯一。不难发现，若令 2 1 λ1 = λ2 = ，α = β = 1，即为改 进的 Euler 公式。可以证明，在[ , ] n n+1 x x 内只取 2 点的龙格—库塔公式精度最高为 2 阶。 4.2 4 阶龙格—库塔公式 要进一步提高精度，必须取更多的点，如取 4 点构造如下形式的公式： ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ = + + + + = + + + = + + = + = + + + + ( , ) ( , ) ( , ) ( , ) ( ) 4 3 4 1 5 2 6 3 3 2 2 1 3 2 2 1 1 1 1 1 1 1 2 2 3 3 4 4 k f x h y hk hk hk k f x h y hk hk k f x h y hk k f x y y y h k k k k n n n n n n n n n n α β β β α β β α β λ λ λ λ （17） 其中待定系数λi αi β i , , 共 13 个，经过与推导 2 阶龙格—库塔公式类似、但更复杂的计 算，得到使局部误差 ( ) ( ) 5 y xn+1 − yn+1 = O h 的 11 个方程。取既满足这些方程、又较简 单的一组λi αi β i , , ，可得

yn-名k+2k+26+) k=f(x.y.) h (18) ka=f(x +hy.+hk 这就是常用的4阶龙格一库塔方法（简称RK方法）。 $5线性多步法 以上所介绍的各种数值解法都是单步法，这是因为它们在计算y时，都贝用到 前一步的值y，单步法的一般形式是 y1=yn+hp(xnyn,h)(n=0,L,.,N-） 19 其中p(x,y,h)称为增量函数，例如Euler方法的增量函数为f(x,y),改进Euler法的 增量函数为 p(x.y.h)=-[f(x.y)+f(x+h.y+hf(x.y) 如何通过较多地利用前面的已知信息，如yn,y-1,.,y,来构造高精度的算法 计算y1,这就是多步法的基本思想。经常使用的是线性多步法。 让我们试验一下r=1,即利用y,y1计算ya4:的情况 从用数值积分方法离散化方程的(4)式 x)-yx)=广fx,x)d 出发，记f(x。,y,)=fn,f(xyn)=f,式中被积函数f(x,y(x)用二节点 (x-,了)，(xn,)的插值公式得到（因x≥xn),所以是外插。 x-X。 (20) -Jl(x-x.-)f.-(x-x.)/-l 此式在区间[x,x+】上积分可得 xh=2人- 于是得到 =y+23f.- (21) 注意到插值公式(20)的误差项含因子(x-x-1(x-xn),在区间[x,x+]上积分后 -184-

-184- ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ = + + = + + = + + = + = + + + ( , ) ) 2 , 2 ( ) 2 , 2 ( ( , ) ( 2 2 ) 6 4 3 2 3 1 2 1 1 1 2 3 4 k f x h y hk hk y h k f x hk y h k f x k f x y k k k k h y n n n n n n n n n （18） 这就是常用的 4 阶龙格—库塔方法（简称 RK 方法）。 §5 线性多步法 以上所介绍的各种数值解法都是单步法，这是因为它们在计算 n+1 y 时，都只用到 前一步的值 n y ，单步法的一般形式是 ( , , ) ( 0,1, , 1) yn+1 = yn + hϕ xn yn h n = L N − （19） 其中ϕ(x, y,h) 称为增量函数，例如 Euler 方法的增量函数为 f (x, y) ，改进 Euler 法的 增量函数为 [ ( , ) ( , ( , ))] 2 1 ϕ(x, y,h) = f x y + f x + h y + hf x y 如何通过较多地利用前面的已知信息，如 n n n r y y y − − , , , 1 L ，来构造高精度的算法 计算 n+1 y ，这就是多步法的基本思想。经常使用的是线性多步法。 让我们试验一下 r = 1，即利用 1 , n n− y y 计算 n+1 y 的情况。 从用数值积分方法离散化方程的（4）式 ∫ + + − = 1 ( ) ( ) ( , ( )) 1 n n x x y xn y xn f x y x dx 出发，记 n n n f (x , y ) = f ， 1 1 1 ( , ) n− n− = n− f x y f ，式中被积函数 f (x, y(x)) 用二节点 ( , ) n−1 n−1 x f ，( , ) n n x f 的插值公式得到（因 ) n x ≥ x ，所以是外插。 [( ) ( ) ] 1 ( , ( )) 1 1 1 1 1 1 − − − − − − = − − − − − + − − = n n n n n n n n n n n n x x f x x f h x x x x f x x x x f x y x f （20） 此式在区间[ , ] n n+1 x x 上积分可得 1 2 2 3 ( , ( )) 1 ∫ = − − + n n x x f h f h f x y x dx n n 于是得到 (3 ) 2 n+1 = n + n − n−1 f f h y y （21） 注意到插值公式（20）的误差项含因子( )( ) n 1 n x − x x − x − ，在区间[ , ] n n+1 x x 上积分后

得出h3,故公式(21)的局部截断误差为O(h3),精度比向前Euler公式提高1阶。 若取r=2,3,.可以用类似的方法推导公式，如对于r=3有 -火+是5-59+37a-91 (22) 其局部截断误差为O(h)。 如果将上面代替被积函数f(x,(x)》用的插值公式由外插改为内插，可进一步减 小误差。内插法用的是y4+,yn,.,yn-r4,取r=1时得到的是梯形公式，取r=3时 可得 h 1=+249以m+19以.-5/+f-) (23) 与(22)式相比，虽然其局部截断误差仍为O(),但因它的各项系数（绝对值）大 为减小，误差还是小了。当然，(23)式右端的f1未知，需要如同向后Euler公式一 样，用选代或校正的办法处理。 $6一阶微分方程组与高阶微分方程的数值解法 6.1 一阶微分方程组的数值解法 设有一阶微分方程组的初值间题 y,=f(x,y,2.,ym) =1,2,.,m) (24) [y;(a)=yio 若记y=0,=0o,m,f=,了，则初值 问题(24)可写成如下向量形式 Iy=f(x.v) (25) y(a)=yo 如果向量函数f(x,y)在区域D: a≤x≤b,y∈R" 连续，且关于y满足Lipschitz条件，即存在L>0,使得对x∈[a,b)],片，乃2eR", /(x,y)-f(x,川≤y-y 那么问题(25)在[a,b]上存在唯一解y=y(x)。 问题(25)与(1)形式上完全相同，故对初值问题(1)所建立的各种数值解法可 全部用于求解问题(25)。 6.2高阶微分方程的数值解法 高阶微分方程的初值问题可以通过变量代换化为一阶微分方程组初值问题。 设有成阶常微分方程初值问题 y=f(x,yy,.,ym-)a≤x≤b a）=o,y(a)=y,.,ym-(a)=w- (26 引入新变量乃=少片=y,少。=y-,问题(26)就化为一阶微分方程初值问题 -185

-185- 得出 3 h ，故公式（21）的局部截断误差为 ( ) 3 O h ，精度比向前 Euler 公式提高 1 阶。 若取 r = 2,3,L可以用类似的方法推导公式，如对于 r = 3 有 (55 59 37 9 ) 24 n+1 = n + n − n−1 + n−2 − n−3 f f f f h y y （22） 其局部截断误差为 ( ) 5 O h 。 如果将上面代替被积函数 f (x, y(x)) 用的插值公式由外插改为内插，可进一步减 小误差。内插法用的是 1 1 , , , n+ n n−r+ y y L y ，取 r = 1时得到的是梯形公式，取 r = 3 时 可得 (9 19 5 ) 24 n+1 = n + n+1 + n − n−1 + n−2 f f f f h y y （23） 与（22）式相比，虽然其局部截断误差仍为 ( ) 5 O h ，但因它的各项系数（绝对值）大 为减小，误差还是小了。当然，（23）式右端的 n+1 f 未知，需要如同向后 Euler 公式一 样，用迭代或校正的办法处理。 §6 一阶微分方程组与高阶微分方程的数值解法 6.1 一阶微分方程组的数值解法 设有一阶微分方程组的初值问题 ⎩ ⎨ ⎧ = = 0 1 2 ( ) ' ( , , , , ) i i i i m y a y y f x y y L y (i =1,2,L,m) （24） 若记 T m y ( y , y , , y ) = 1 2 L ， T m y ( y , y , , y ) 0 = 10 20 L 0 ， T m f ( f , f , , f ) = 1 2 L ，则初值 问题（24）可写成如下向量形式 ⎩ ⎨ ⎧ = = 0 ( ) ' ( , ) y a y y f x y （25） 如果向量函数 f (x, y) 在区域 D ： m a ≤ x ≤ b, y ∈ R 连续，且关于 y 满足 Lipschitz 条件，即存在 L > 0 ，使得对∀x ∈[a,b]， m y1, y2 ∈ R ， 都有 1 2 1 2 f (x, y ) − f (x, y ) ≤ L y − y 那么问题（25）在[a,b] 上存在唯一解 y = y(x) 。 问题（25）与（1）形式上完全相同，故对初值问题（1）所建立的各种数值解法可 全部用于求解问题（25）。 6.2 高阶微分方程的数值解法 高阶微分方程的初值问题可以通过变量代换化为一阶微分方程组初值问题。 设有m 阶常微分方程初值问题 ⎩ ⎨ ⎧ = = = = ≤ ≤ − − − ( 1) 0 (1) ( 1) 0 0 ( ) ( 1) ( ) , '( ) , , ( ) ( , , ', , ) m m m m y a y y a y y a y y f x y y y a x b L L （26） 引入新变量 ( 1) 1 2 , ', , − = = = m m y y y y L y y ，问题（26）就化为一阶微分方程初值问题

= y(a)=yo 2= (a)=" (27) y-i(a）=yg"-2 ym=fx,yn） y(a)=yim-1) 然后用6.1中的数值方法 以得到问题(26)的数值解 常常是所 常微分方程组初值 具体地说。 =Ay+( (28) dx 其中，①∈R,A为m阶方阵。若矩阵A的特征值A(=1,2,.,m)满足关系 Re,nRe 则称方程组(28)为刚性方程组或Sf方程组，称数 s=Re min Re 为刚性比。对刚性方程组，用前面所介绍的方法求解，都会遇到本质上的困难，这是由 数值方法本身的稳定性限制所决定的。理论上的分析表明，求解刚性问题所选用的数伯 方法最好是对步长h不作任何限制。 7 Matlab解法 71 Matlab数值解 7.1.1非刚性常微分方程的解法 Matlab的工具箱提供了几个解非刚性常微分方程的功能函数，如ode45,ode23, ode113,其中ode45采用四五阶RK方法，是解非刚性常微分方程的首选方法，ode23 采用二三阶RK方法，ode113采用的是多步法，效率一般比ode45高。 Matlab的工具箱中没有Euler方法的功能函数。 (I)对简单的一阶方程的初值问题 y=f(x,y) (x)=% 改进的Euler公式为 yp=y+hf(x.y.) y=y.+hf(x+h.y) y-0,以 我们自己编写改进的Euler方法函数eulerpro.m如下： -186

-186- ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ = = = = = = = = − − − − ( 1) 1 0 ( 2) 1 1 0 (1) 2 3 2 0 1 2 1 0 ' ( , , , ) ( ) ' ( ) ' ( ) ' ( ) m m m m m m m m y f x y y y a y y y y a y y y y a y y y y a y L M M （27） 然后用 6.1 中的数值方法求解问题（27），就可以得到问题（26）的数值解。 最后需要指出的是，在化学工程及自动控制等领域中，所涉及的常微分方程组初值 问题常常是所谓的“刚性”问题。具体地说，对一阶线性微分方程组 Ay (x) dx dy = + Φ （28） 其中 y R A m ,Φ ∈ , 为m 阶方阵。若矩阵 A 的特征值 (i 1,2, ,m) λi = L 满足关系 Re 0 (i 1,2, ,m) λi > 则称方程组（28）为刚性方程组或 Stiff 方程组，称数 max | Re | / min | Re | 1 1 i i m i i m s λ λ ≤ ≤ ≤ ≤ = 为刚性比。对刚性方程组，用前面所介绍的方法求解，都会遇到本质上的困难，这是由 数值方法本身的稳定性限制所决定的。理论上的分析表明，求解刚性问题所选用的数值 方法最好是对步长 h 不作任何限制。 §7 Matlab 解法 7.1 Matlab 数值解 7.1.1 非刚性常微分方程的解法 Matlab 的工具箱提供了几个解非刚性常微分方程的功能函数，如 ode45，ode23， ode113，其中 ode45 采用四五阶 RK 方法，是解非刚性常微分方程的首选方法，ode23 采用二三阶 RK 方法，ode113 采用的是多步法，效率一般比 ode45 高。 Matlab 的工具箱中没有 Euler 方法的功能函数。 （I）对简单的一阶方程的初值问题 ⎩ ⎨ ⎧ = = 0 0 ( ) ' ( , ) y x y y f x y 改进的 Euler 公式为 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = + = + + = + + ( ) 2 1 ( , ) ( , ) n 1 p q q n n p p n n n y y y y y hf x h y y y hf x y 我们自己编写改进的 Euler 方法函数 eulerpro.m 如下： function [x,y]=eulerpro(fun,x0,xfinal,y0,n); if nargin<5,n=50;end

0928 for i=1:n x(i+l 例1用改进的Euler方法求解 (0≤x≤0.5)，0)=1 解 在atlab命令窗口输入： x,y]=e ulerpro('doty',0,0.5.1,10) ,ode113的使用 [t,y]=solver ('F 这里sol ve 为0de45,odc23,ode113,输入参数F是用M文件定义的微分方程 y=f(x,y)右端的函数。tspans=[t0,tfinal]是求解区间，y0是初值。 用RK方法求解 y=-2y+2x+2x,(0≤x≤0.5)，y0)=1 解同样地编写函数文件doy.m如下： 在Matlab命令窗口输入： [x,y]=ode45('doty',0,0.5,1) 即可求得数值解。 7.12刚性常微分方程的解法 Matlab的工具箱提供 几个解刚性常微分方程的功能函数，如ode15s,0de23s, odc23L,0de23b,这些函数的使用同上述非刚性微分方程的功能函数。 7.13高阶微分方程y=f(1,八，.，y-)解法 例3考忠初值问题 y"-3y"-yy=0y(0)=0y(0)=1y"(0)=-1 解()如果设=,片2=y，=，那么 y'=y3 y,(0)=0 y2= 5(0)=1 y3=3y3+y2y y,(0)=-1 初值问题可以写成Y=F(L,Y),Y(O)=Y。的形式，其中 Y=[y2] (i)把一阶方程组写成接受两个参数1和y,返回一个列向量的M文件Fm: function dy=F(t,y); -187

-187- h=(xfinal-x0)/n; x(1)=x0;y(1)=y0; for i=1:n x(i+1)=x(i)+h; y1=y(i)+h*feval(fun,x(i),y(i)); y2=y(i)+h*feval(fun,x(i+1),y1); y(i+1)=(y1+y2)/2; end 例1 用改进的Euler方法求解 y' 2y 2x 2x 2 = − + + ，(0 ≤ x ≤ 0.5) ， y(0) = 1 解 编写函数文件 doty.m 如下： function f=doty(x,y); f=-2*y+2*x^2+2*x; 在Matlab命令窗口输入： [x,y]=eulerpro('doty',0,0.5,1,10) 即可求得数值解。 （II）ode23，ode45，ode113的使用 Matlab的函数形式是 [t,y]=solver('F',tspan，y0) 这里solver为ode45，ode23，ode113，输入参数 F 是用M文件定义的微分方程 y'= f (x, y) 右端的函数。tspan=[t0,tfinal]是求解区间，y0是初值。 例2 用RK方法求解 y' 2y 2x 2x 2 = − + + ，(0 ≤ x ≤ 0.5) ， y(0) = 1 解 同样地编写函数文件 doty.m 如下： function f=doty(x,y); f=-2*y+2*x^2+2*x; 在Matlab命令窗口输入： [x,y]=ode45('doty',0,0.5,1) 即可求得数值解。 7.1.2 刚性常微分方程的解法 Matlab的工具箱提供了几个解刚性常微分方程的功能函数，如ode15s，ode23s， ode23t，ode23tb，这些函数的使用同上述非刚性微分方程的功能函数。 7.1.3 高阶微分方程 ( , , ', , ) ( ) ( −1) = n n y f t y y L y 解法 例 3 考虑初值问题 y'''−3y''−y' y = 0 y(0) = 0 y'(0) =1 y''(0) = −1 解 （i）如果设 , ', '' 1 2 3 y = y y = y y = y ，那么 ⎪ ⎩ ⎪ ⎨ ⎧ = + = − = = = = ' 3 (0) 1 ' (0) 1 ' (0) 0 3 3 2 1 3 2 3 2 1 2 1 y y y y y y y y y y y 初值问题可以写成 0 Y '= F(t,Y ),Y (0) = Y 的形式，其中 [ ; ; ] 1 2 3 Y = y y y 。 （ii）把一阶方程组写成接受两个参数t 和 y ，返回一个列向量的 M 文件 F.m： function dy=F(t,y);

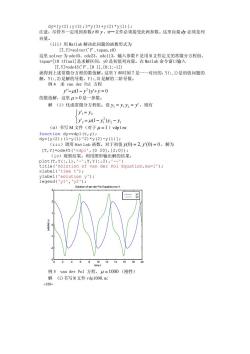
向量。 ii),用at1ab解决此问题的函数形式为 [T,Y]=solver( F,tspan,yo) 这里s0内是求解区 00 0是初值列向最】 金令窗口输) T,Y]=ode45F',[01,[0:1:-1) 就得到上述常微分方程的数值解。这里yY和时刻T是一一对应的，Y(:,1)是初值问题的 解，Y(:,2)是解的导数，Y(:,3)是解的二阶导数。 例4求van der Pol方程 y"-4(1-y2)y+y=0 的数值解，这里>0是一参数 解()化成常微分方程组。设y-y,乃2=少，则有 yi=y: y,=uI-y)y、-y (i)书写M文件（对于=1)vdpl.m yc2,Yy1Yy2)-y1: (iii)调用Mat1ab函数。对于初值y0)-2,y(0)=0,解为 [T,Y]=ode45('vdp1',[0201,[2:0]): (iv)观察结果。利用图形输出解的结果： Hi86ilot6oi2quatiom,au-1: on of ven der Pol Equation,mu= 026日0,26动 例5 van der Pol方程，H=1000(刚性) -1)书写M文件vd100

-188- dy=[y(2);y(3);3*y(3)+y(2)*y(1)]; 注意：尽管不一定用到参数t 和 y ，M—文件必须接受此两参数。这里向量 dy 必须是列 向量。 （iii）用 Matlab 解决此问题的函数形式为 [T,Y]=solver('F',tspan,y0) 这里 solver 为 ode45、ode23、ode113，输入参数 F 是用 M 文件定义的常微分方程组， tspan=[t0 tfinal]是求解区间，y0 是初值列向量。在 Matlab 命令窗口输入 [T,Y]=ode45('F',[0 1],[0;1;-1]) 就得到上述常微分方程的数值解。这里 Y 和时刻 T 是一一对应的，Y(:,1)是初值问题的 解，Y(:,2)是解的导数，Y(:,3)是解的二阶导数。 例 4 求 van der Pol 方程 '' (1 ) ' 0 2 y −μ − y y + y = 的数值解，这里 μ > 0是一参数。 解 （i）化成常微分方程组。设 , ' 1 2 y = y y = y ，则有 ⎩ ⎨ ⎧ = − − = 2 1 2 2 1 1 2 ' (1 ) ' y y y y y y μ （ii）书写 M 文件（对于 μ =1）vdp1.m: function dy=vdp1(t,y); dy=[y(2);(1-y(1)^2)*y(2)-y(1)]; （iii）调用 Matlab 函数。对于初值 y(0) = 2, y'(0) = 0 ，解为 [T,Y]=ode45('vdp1',[0 20],[2;0]); （iv）观察结果。利用图形输出解的结果： plot(T,Y(:,1),'-',T,Y(:,2),'-') title('Solution of van der Pol Equation,mu=1'); xlabel('time t'); ylabel('solution y'); legend('y1','y2'); 0 2 4 6 8 10 12 14 16 18 20 -3 -2 -1 0 1 2 3 Solution of van der Pol Equation,mu=1 time t solution y y1 y2 例 5 van der Pol 方程， μ =1000 （刚性） 解 (i)书写 M 文件 vdp1000.m: