《金融经济学原理》课程教学课件（PPT讲稿）无套利定价之欧式期权（1）

无套利定价 期权定价 第一部分：欧式期权定价 1

无套利定价 期权定价 第一部分：欧式期权定价 1

欧式期权 ·假设x是资产在t=1的支付，S是资产在t=0的价值。 定义（欧式期权） An European call(put)option on the stock with strike price K and maturity date t is a security that gives the buyer the right to buy (sell)the stock at maturity at price K. 课堂练习：根据上面的信息，在草稿本上写出欧式看涨和看跌期权 的oayoff;并且画出payoff的图。 2

欧式期权 • 假设෩X是资产在t=1的支付，S是资产在t=0的价值。 定义（欧式期权） 课堂练习：根据上面的信息，在草稿本上写出欧式看涨和看跌期权 的payoff；并且画出payoff的图。 An European call (put) option on the stock with strike price K and maturity date t is a security that gives the buyer the right to buy (sell) the stock at maturity at price K . 2

美式期权 定义（美式期权）An American call(put)option on the stock with strike price K and maturity date t is a security that gives the buyer the right to buy(sell)the stock at any time before and including the maturity date at price K. 一 些符号： 符号 含义 c(S.K) 欧式看涨期权在t=0的价值 C(S,9 美式看涨期权在t=0的价值 p(S.K) 欧式看跌期权在t=0的价值 P(S,9 美式看跌期权在t=0的价值 3

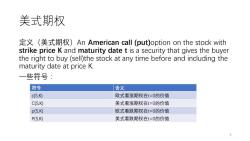
美式期权 定义（美式期权）An American call (put)option on the stock with strike price K and maturity date t is a security that gives the buyer the right to buy (sell)the stock at any time before and including the maturity date at price K. 一些符号： 符号 含义 c(S,K) 欧式看涨期权在t=0的价值 C(S,K) 美式看涨期权在t=0的价值 p(S,K) 欧式看跌期权在t=0的价值 P(S,K) 美式看跌期权在t=0的价值 3

欧式期权价值的无套利性质 ·根据无套利定价原理，对于两个资产A和B,X4w≥XBw),那么 S4≥SB使用无套利定价理论，期权价值满足如下的关系。 定理1c(S,K)和p(S,K)是非负的； =8-M20,=K-0420 定理2c(S,K)对于K是非递增的，p(S,K)对K是非递减的； Proof::K>K2,max[0,X-K≤max[0,产-K].Thus,c(S,K)≤c(S,K2)

欧式期权价值的无套利性质 • 根据无套利定价原理，对于两个资产A和B，𝑋𝐴 𝑤 ≥ 𝑋𝐵 𝑤 , 那么 𝑆𝐴 ≥ 𝑆𝐵.使用无套利定价理论，期权价值满足如下的关系。 定理1 𝑐 𝑆,𝐾 和𝑝 𝑆,𝐾 是非负的； 定理2 𝑐 𝑆,𝐾 对于K是非递增的，𝑝 𝑆,𝐾 对K是非递减的； 4

定理3c(S,K)和p(S,K)对于K是凸(Convex)的； Proof::K1>K2和a∈(0,1)， max0,X-aK+a-aK=maxf0,a(区-K）+a-a(&-K] <amax(1-a)max0, 换句话说，max本身是一个凸函数。 定理4令0≥0为N个资产的投资份额，则 c(S0,KT0)≤∑0：c(S,K),p(sr8,KT0)≤∑0：~pS,K) 即投资组合期权的价值小于期权投资组合价值的总和。 经济学含义：大盘指数期权比个股期权比例加总便宜 5

定理3 𝑐 𝑆,𝐾 和 𝑝 𝑆,𝐾 对于K是凸(Convex)的； Proof: ∀𝐾1 > 𝐾2和𝛼 ∈ (0,1), 换句话说，max本身是一个凸函数。 定理4 令𝜃 ≥ 0 为N个资产的投资份额，则 即投资组合期权的价值小于期权投资组合价值的总和。 经济学含义：大盘指数期权比个股期权比例加总便宜 5

证明：股票的价格为S,i=1,.,N,以其为基础资产的期权执行 价为K;。股票及其对应的期权头寸为9：。0时股票组合的价值为 S0,1时的支付为X0。 投资组合期权的支付为 at-网-mya(民-) 期权的投资组合支付为 max0,文-7g=∑，max0,X-K个 根据支付方程的凸性，我们有 mr0a(x-k刘s∑4m包成-k个 6

证明：股票i的价格为𝑆𝑖，𝑖 = 1, ⋯ , 𝑁, 以其为基础资产的期权执行 价为𝐾𝑖。股票i及其对应的期权头寸为𝜃𝑖。0时股票组合的价值为 S 𝑇𝜃, 1时的支付为𝑋𝜃。 投资组合期权的支付为 期权的投资组合支付为 根据支付方程的凸性，我们有 6

定理5S≥c(S,K) 定理6无险资产的回报率为，则6，幻≥包，S-,] 证明：构建一个投资组合 1)买入一单位的股票 2)）卖空无风险债券 t=0时，投资组合的价值为 K S一1+F t=1时，投资组合的价值为文-K t=1时，支付产≥max[0,文-K≥文-K 根据无套利定价原理 t=0时，价值S≥S,)≥S-, K 1+TF

定理5 𝑆 ≥ 𝑐 𝑆 , 𝐾 定理6 无风险资产的回报率为 𝑟𝐹，则 证明：构建一个投资组合 1）买入一单位的股票 2）卖空 K 1+𝑟𝐹 无风险债券 t=0 时，投资组合的价值为 t=1 时，投资组合的价值为 t=1 时， 支付 根据无套利定价原理 t=0 时， 价值 7

期权价值合理范围 又由于期权价值非负c(S,K)≥0。因此满足无套利假设的均衡欧 式期权价值应该在如下的范围 9248≥xO8-,司

期权价值合理范围 又由于期权价值非负 𝑐 𝑆,𝐾 ≥ 0。因此满足无套利假设的均衡欧 式期权价值应该在如下的范围 8

期权平价公式（证明一定是model free) K c(S,K)+1+rr =p(S,K)+S 证明1：无套利定价原理 考虑如下的投资组合： 1）)持有一个执行价为K的看涨期权和，K无风险债券； 它在=0时间点的价值为(S,0+ 1+rE 2)持有一个执行价为K的看跌期权和1单位的股票； 它在t=0时间点的价值为p(S,K)+S 9

期权平价公式（证明一定是model free） 证明1：无套利定价原理 考虑如下的投资组合： 1）持有一个执行价为K的看涨期权和 K 1+𝑟𝐹 无风险债券； 它在t=0时间点的价值为𝑐 𝑆,𝐾 + 𝐾 1+𝑟𝐹 2）持有一个执行价为K的看跌期权和1单位的股票； 它在t=0时间点的价值为𝑝 𝑆,𝐾 + 𝑆 9

·投资组合的支付如下表所示 ≤K X>K (1) max[0,]+K =K max[0,京-K]+K=元 (2) maxf0,K-]+永=K max[0,K-]+文=X ·显然，组合1和组合2的支付是相同的。因此，根据无套利定价原 理，它们的成本也是相同的，即 K c(S,K)+1+rF =p(S,K)+S 10

• 投资组合的支付如下表所示 • 显然，组合1和组合2的支付是相同的。因此，根据无套利定价原 理，它们的成本也是相同的，即 10