《计算机应用基础》课程教学资源（PPT课件讲稿）第四章 数制与信息编码

山求理2大军 SHANDONG UNIVERSITY OF TECHNOLOGY 第二篇系统平台与计算环境 第4章数制与信息编码

第二篇系统平台与计算环境 第4章 数制与信息编码

0 目录 计草机利学与校未学网 数制及其转换 数值型数据的表示及处理 文字的表示及处理 多媒体信息的表示及处理 5. 条形码和RFID

目录 4. 多媒体信息的表示及处理 3. 文字的表示及处理 2. 数值型数据的表示及处理 1. 数制及其转换 5. 条形码和RFID

1.数制及其转换 0 件菜凤利学与拉未学腐 口常用数制 口数制的转换 口二进制的运算规则

1.数制及其转换 ❑ 常用数制 ❑ 数制的转换 ❑ 二进制的运算规则

常用数制 0 计草机利学与校术学网 计数：十进制。 计时：六十进制。 月到年的进制：十二进制。 季度到年的进制：四进制。 在计算机内部用二进制数码表示各种数据，在 计算机程序的编写中有时采用八进制和十六进制

常用数制 计数：十进制。 计时：六十进制。 月到年的进制：十二进制。 季度到年的进制：四进制。 在计算机内部用二进制数码表示各种数据，在 计算机程序的编写中有时采用八进制和十六进制

常用数制 什草凤利学与拉未学丽 数码：一组用来表示某种数制的符号。 基数：数制所使用的数码个数称为“基数” 或“基”，常用“R”表示，称R进制。 十进制 R=10,包含数码：0,1,2,3,4,5,6,7,8,9 二进制 R=2,包含数码：0,1 八进制 R=8,包含数码：0,1,2,3,4,5,6,7 十六进制R=16,包含数码：0，9，A,B,C,D,E,F 《逢R进一，借一当R

5 ◼ 数码：一组用来表示某种数制的符号。 ◼ 基数：数制所使用的数码个数称为“基数” 或“基”，常用“R”表示，称R进制。 十进制 R=10， 包含数码:0,1,2,3,4,5,6,7,8,9 二进制 R=2 ， 包含数码: 0,1 八进制 R=8 ， 包含数码: 0,1,2,3,4,5,6,7 十六进制 R=16 ，包含数码: 0,.,9,A,B,C,D,E,F “逢R进一，借一当R” 常用数制

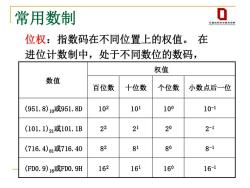
常用数制 0 计草机利学与技术学腐 位权：指数码在不同位置上的权值。在 进位计数制中，处于不同数位的数码， 权值 数值 百位数 十位数 个位数 小数点后一位 (951.8)1或951.8D 102 101 100 10-1 (101.1)21或101.1B 22 21 20 2-1 (716.4)81或716.40 82 81 80 81 (FD0.9)16或FD0.9H 162 161 160 16-1

6 位权：指数码在不同位置上的权值。 在 进位计数制中，处于不同数位的数码， 代表的数值不同。 数值 权值 百位数 十位数 个位数 小数点后一位 (951.8)10或951.8D 102 101 100 10-1 (101.1)21或101.1B 2 2 2 1 2 0 2 -1 (716.4)81或716.4O 8 2 8 1 8 0 8 -1 (FD0.9)16或FD0.9H 162 161 160 16-1 常用数制

常用数制 什草凤利学与拉未学脑 数制 十进制数 二进制数 八进制数 十六进制数 数码 0~9 0~1 0~7 0-9,A~F,a~f 基 10 2 8 16 权 10°，10,102， .2°，2,22，. 8°，81,82，. 16°，16,162， 表示 -八进制：4275=4*83+2*82+7*81+5*801+14*16° 特点 逢十进一 逢二进一 逢八进一 逢十六进一

数制 基 权 表示 数码 特点 10º ，10¹，10²，. 十进制数 0~9 10 逢十进一 二进制数 0~1 2 2º ，2¹，2²，. 逢二进一 八进制数 0~7 8 8º ，8¹，8²，. 逢八进一 十六进制数 0~9,A~F,a~f 16 16º ，16¹，16²，. 逢十六进一 十六进制： 十进制： 八进制： 二进制：4956= 4275=4*8³+2*8² +7*8¹+5*8º 1011=1*2³+0*2² +1*2¹+1*2º 81AE=8*16³+1*16² +10*16¹+14*16º 4*10³+9*10² +5*10¹+6*10º 常用数制

十进制、二进制、八进制、十六进制之间的对应关系 计算机利学与技术学腐 十进制 二进制 八进制 十六进制 十进制 二进制 八进制 十六进制 0 01 01 0 9 1001 1 1 10 1010 1 9A 23 11 1011 01000 234567 23 12 1100 漫 4 4 13 1101 1 567 5 14 1110 67 15 1111 16 10000 1000 161704 10 8 10 8 17 10001 11

十进制、二进制、八进制、十六进制之间的对应关系 十进制 二进制 八进制 十六进制 十进制 二进制 八进制 十六进制 0 1 2 3 4 5 6 7 8 0 1 10 11 100 101 110 111 1000 0 1 2 3 4 5 6 7 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1001 1010 1011 1100 1101 1110 1111 10000 10001 11 12 13 14 15 16 17 20 21 9 A B C D E F 10 11

数制的转换 凤利学与技学 >二进制、八进制、十六进制数转化为十进制数 对于任何一个二进制数、八进制数、十六进制数可以写出它的按权 展开式，再进行计算即可。 例如： (1111.11)2 =1×23+1×22+1×21+1×20+1×2-1+1×2-2=15.75 (A10B.8)16 =10×163+1×162+0×161+11×160+8×161=41227.5

数制的转换 ➢ 二进制、八进制、十六进制数转化为十进制数 对于任何一个二进制数、八进制数、十六进制数可以写出它的按权 展开式，再进行计算即可。 例如： （1111.11）2 = 1×2 3+1×2 2+1×2 1+1×2 0 +1×2 -1 +1×2 -2=15.75 （A10B.8）16 =10×163 + 1×162+ 0×161 +11×160 +8×16-1= 41227.5

十进制数转化为R进制数 计草机利学与校术学网 对于整数部分采用除R取余法，即逐次除以R,直至商为0 得出的余数倒排，即为R进制各位的数码。 示例1：十进制转换为八进制 最低位 8 75 3 (75)。=(113)为 8 9 1 (113)8 8 1 1 =1×82+1×81+3×80 最高位

十进制数转化为R进制数 对于整数部分采用除R取余法，即逐次除以R，直至商为0 ，得出的余数倒排，即为R进制各位的数码。 (75)10=(113)8 示例1：十进制转换为八进制 75 9 1 8 8 8 3 1 1 0 最高位 最低位 （113）8 =1×8 2＋1×8 1＋3×8 0