华南农业大学：《高等数学》课程PPT教学课件（经济数学B上册）经济数学第29次授课提纲

上次课内容复习： 1、定积分的定义 ∫。fax)dx=lim∑f5)A 2、定积分存在的必要条件和两个充分条件； 3、定积分的几何意义： 4、定积分的八条性质

上次课内容复习： 1、定积分的定义 ( )d b a f x x  0 1 lim ( ) n i i i f x   → = =   2、定积分存在的必要条件和两个充分条件； 3、定积分的几何意义； 4、定积分的八条性质

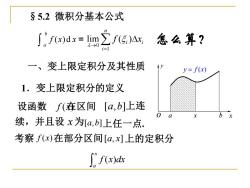
§5.2微积分基本公式 ∫f)dx=m∑f(5,)A怎么算？ 一、变上限定积分及其性质 y=f(x) 1.变上限定积分的定义 设函数f(在区间[a,b]上连 o a 6 续，并且设x为[a,b]上任一点. 考察f(x)在部分区间[a,x)]上的定积分 ∫fx)ds

§5.2 微积分基本公式 ( )d b a f x x  0 1 lim ( ) n i i i f x   → = =   怎么算？ 一、变上限定积分及其性质 1．变上限定积分的定义 f (x) [a,b] x [ , ] a b f x( ) [ , ] a x ( ) x a f x dx  设函数 在区间 上连 续，并且设 为 上任一点. 考察 在部分区间 上的定积分 o a x b x y y f x = ( )

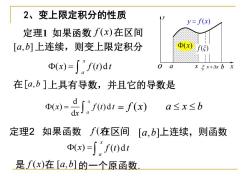
2、变上限定积分的性质 y=f(x) 定理1如果函数f(x)在区间 [a,b]上连续，则变上限定积分 ()f) Φ(x)=∫f)dt x5x+△xbx 在[a,b]上具有导数，并且它的导数是 W-J0d=f(x) a≤x≤b 定理2 如果函数f(在区间[a,b]上连续，则函数 (x)=∫f)di 是f(x)在[a,b]的一个原函数

a x  x x + x ( ) x f ( ) ξ y f x = ( ) o y b 2、变上限定积分的性质 f (x) [a,b] ( ) ( )d x a  = x f t t  d ( ) ( )d d x a x f t t x  =  f (x) a  x  b 在[ a b, ]上具有导数，并且它的导数是 定理1 如果函数 在区间 上连续，则变上限定积分 = [a,b] (x) = ( )d x a f t t  是 f (x)在 的一个原函数. f (x) 定理2 如果函数 在区间 [a,b] 上连续，则函数

例1设f(x)在[0，+∞)内连续且f(x)>0,证明函 数 。fe0dr 、 F(x) ∫。fd)dt 在[0，+∞)内为单调增加函数 例2设f(x)是连续函数，F(x)=∫。f)di 求F'(x)

f (x) f x( )  0 0 0 ( )d ( ) ( )d x x tf t t F x f t t =   例1 设 在 内为单调增加函数. 在 0,+) 内连续且 ,证明函 数 0,+) f x( ) ( ) ( )d x F x xf t t =  0 F(x) 例2 设 是连续函数， 求

例3若f(连续，且u=(x),v=v(x)可导， 则 fdi=fpe)-a]ae 4E知y广水， dx [e"di 例5求极限 lim* x-→0

f x( ) u u x v v x = = ( ), ( )     ( ) ( ) d ( )d ( ) '( ) ( ) '( ) d v x u x f t t f v x v x f u x u x x = −  例3 若 连续，且 可导， 则 d d y x 例4 已知 ，求 ． 4 2 2 1 1 x x y dt t = +  例5 求极限 1 2 -t cos 2 0 e d lim x x t → x  ．

二、牛顿一莱布尼茨公式 定理1如果函数F(是连续函数f(x)在区间 [a,b处的一个原函数，则 ∫。f)dx=Fb)-Fa dx 6求3 √3 =arctanx 1 = arctan 3-arctan(-1)

二、牛顿—莱布尼茨公式 ． F(x) f (x) [ , ] a b ( )d b a f x x =  F(b) − F(a) 定理1 如果函数 是连续函数 上的一个原函数，则 在区间 例6 求 解: x x x arctan 1 3 d 1 2 = + − 1 3 − = arctan 3 − arctan(−1) 3  =  12 7 ) = 4 (  − −

例7.计算正弦曲线y=sinx在[0，π]上与x轴所围成 的面积 yy=sinx 解：A=∫sinxdx =-csx0=-1-]=20 πx 例8求∫V1+cos2xdx

例7. 计算正弦曲线 的面积 . 解:  =  0 A sin xdx = −cos x 0  = −[−1−1] = 2 y o x y = sin x  例8 求 0 1 cos 2 d x x  + 

例9设f(为分段函数，在[0,2]上连续， 2-x2 0≤x≤1 f(x)= 1<x≤2 求∫。f(x)dx

f x( ) [0, 2] ( ) x x f x x x  −   =     2 2 0 1 1 2 f x x ( )d  2 0 例9 设 为分段函数,在 求 . 上连续

本次课内容小结 作业：习题5-2 1.微积分基本公式 设f(x)∈C[a,b],且F(x)=f(x),则有 ∫fax)dx=f5b-a)）=F'(5b-a)=Fb)-Fa) 积分中值定理 微分中值定理 牛顿-莱布尼兹公式 2.变限积分求导公式

本次课内容小结 设 f (x)C[a,b], 且F(x) = f (x), 则有 1. 微积分基本公式 =  f x x b a ( )d 积分中值定理 = F()(b − a) = F(b) − F(a) 微分中值定理 f ()(b − a) 牛顿 – 莱布尼兹公式 2. 变限积分求导公式 作业：习题5-2