南京大学：《计算机问题求解》课程教学资源（PPT课件讲稿）递归及其数学基础（part-1）

计算机问题求解一论题2-5 递归及其数学基础 2020年03月26日

计算机问题求解 – 论题2-5 - 递归及其数学基础 2020年03月26日

问题1： 以Hanoi Tower为例，说说你对“递归思想”、 “递归过程”、“递归式”的理解

以Hanoi Tower为例，说说你对“递归思想”、 “递归过程”、“递归式”的理解

最简单的解递归式的方法-回朔 T(1)=1 T(n)=2T(n-1)+1 T()-2T(-1)+ 2T(m-1)=4Tn-2)2 4Tm-2)=8Tm-3)+4人 Tn)=2"-1 2m-2T(2)(2m-1T(1)+2n-2

最简单的解递归式的方法 – 回朔

问题2： 这里的解递归武和前一次讨论中的解 递归式有什么区别？

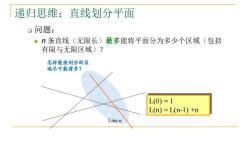
递归思维：直线划分平面 口问题： ·n条直线（无限长）最多能将平面分为多少个区域（包括 有限与无限区域)？ 怎样能使划分的区 域尽可能得多？ L(0)=1 L(n)=L(n-1)+n Line n

递归思维：直线划分平面 ❑ 问题： ◼ n 条直线（无限长）最多能将平面分为多少个区域（包括 有限与无限区域）？ Line n 怎样能使划分的区 域尽可能得多？ L(0) = 1 L(n) = L(n-1) +n

用回朔的办法解递归 L(m)=L(-1)+n =L(n-2)+(n-1)+n =L(n-3)+(m-2)+(n-1)+n =L(0)+1+2+..+(n-2)t(n-1)tn L(m=n(n+)/2+1

用回朔的办法解递归 L(n) = L(n-1)+n = L(n-2)+(n-1)+n = L(n-3)+(n-2)+(n-1)+n = …… = L(0)+1+2+……+(n-2)+(n-1)+n L(n) = n(n+1)/2 + 1

递归思维：Josephus问题 Live or die,it's a problem! Legend has it that Josephus wouldn't have lived to become famous without his mathematical talents. During the Jewish Roman war,he was among a band of 41 Jewish rebels trapped in a cave by the Romans. Preferring suicide to capture,the rebels decided to form a circle and, proceeding around it,to killevery third emaining person until no one was left. 0 But Josephus,along with an unindicted co-conspirator,wanted none of this suicide nonsense;so he quickly calcdlated where he and his friend should stand in the vicious circle. We use a simpler version: “every second

递归思维：Josephus 问题 ◼ Live or die, it’s a problem! ❑ Legend has it that Josephus wouldn't have lived to become famous without his mathematical talents. ❑ During the Jewish Roman war, he was among a band of 41 Jewish rebels trapped in a cave by the Romans. ❑ Preferring suicide to capture, the rebels decided to form a circle and, proceeding around it, to kill every third remaining person until no one was left. ❑ But Josephus, along with an unindicted co-conspirator, wanted none of this suicide nonsense; so he quickly calculated where he and his friend should stand in the vicious circle. We use a simpler version: “every second

试试看：n=10 一及 survivor J(10)=5

试试看：n=10 1 8 7 6 2 4 5 10 3 9 1 7 5 9 3 1 7 5 9 3 survivor J(10)=5

For 2n Persons (n=1,2,3,...) 2- 2n-1 3 2u-1X-XL13 2n- 5 n persons left\ k+1 下一轮将如何进行？它和上一轮有什么相同之处？

For 2n Persons (n=1,2,3,... ) 1 2n 2 2n-1 3 k+1 k k-1 1 2n-1 3 2n-3 5 k+3 k+1 k-1 n persons left 下一轮将如何进行？它和上一轮有什么相同之处？

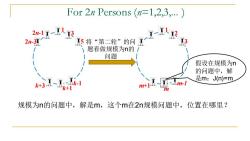
For 2n Persons (n=1,2,3,...) 2-1-1x3 2n-3X 5将“第二轮”的问 题看做规模为n的/ 问题 假设在规模为n 的问题中，解 是m:J(n)=m k+3A- X-Ak-1 k+1 规模为n的问题中，解是m,这个m在2n规模问题中，位置在哪里？

For 2n Persons (n=1,2,3,... ) 1 2n-1 3 2n-3 5 k+3 k+1 k-1 1 2 3 m+1 m m-1 将“第二轮”的问 题看做规模为n的 问题 规模为n的问题中，解是m，这个m在2n规模问题中，位置在哪里？ 假设在规模为n 的问题中，解 是m：J(n)=m