新疆大学：《电力系统分析》课程教学课件（暂态部分）第三章 电力系统三相短路电流的实用计算

条大蓉 Xinjiang University 第三章 电力系统三相短路电流的实用计算 电壳工程学院 电气工程及其自动化专业

第三章 电力系统三相短路电流的实用计算 第三章 电力系统三相短路电流的实用计算 电力系统三相短路电流的实用计算 Xinjiang University 电气工程学院 电气工程及其自动化专业

三相短路实用计算的基本假设 (1)电势都同相位：短路过程中各发电机之间不发生摇 摆，并认为所有发电机的电势都同相位。 (2)负荷近似估计：或当作恒定电抗，或当作某种临时 附加电源，视具体情况而定。 (3)不计磁路饱和：系统各元件的参数都是恒定的，可 以应用叠加原理

三相短路实用计算的基本假设 三相短路实用计算的基本假设 （1）电势都同相位：短路过程中各发电机之间不发生摇 摆，并认为所有发电机的电势都同相位。 （2）负荷近似估计：或当作恒定电抗，或当作某种临时 附加电源，视具体情况而定。 （3）不计磁路饱和：系统各元件的参数都是恒定的，可 以应用叠加原理

(4)对称三相系统：除不对称故障处出现局部的不对称以外 ，实际的电力系统通常都当做是对称的。 (5)纯电抗表示：忽略高压输电线的电阻和电容，忽略变压 器的电阻和励磁电流（三相三柱式变压器的零序等值电路除 外)，加上所有发电机电势都同相位的条件，这就避免了复 数运算。 (6)金属性短路：短路处相与相（或地）的接触往往经过一 定的电阻（如外物电阻、电弧电阻、接触电阻等），这种电 阻通常称为“过渡电阻”。所谓金属性短路，就是不计过渡电 阻的影响，即认为过渡电阻等于零的短路情况

（4）对称三相系统：除不对称故障处出现局部的不对称以外 ，实际的电力系统通常都当做是对称的。 （5）纯电抗表示:忽略高压输电线的电阻和电容，忽略变压 器的电阻和励磁电流（三相三柱式变压器的零序等值电路除 外），加上所有发电机电势都同相位的条件，这就避免了复 数运算。 （6）金属性短路:短路处相与相（或地）的接触往往经过一 定的电阻（如外物电阻、电弧电阻、接触电阻等），这种电 阻通常称为“过渡电阻”。所谓金属性短路，就是不计过渡电 阻的影响，即认为过渡电阻等于零的短路情况

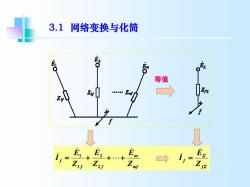
3.1网络变换与化简 等值 i * 它2+ E i,= Z

3.1 网络变换与化简 网络变换与化简 等值 Σ Σ f f mf m f f f Z E I Z E Z E Z E I & & & L & & & = + + + = 2 2 1 1

1.网络的等值变换 (1)星网变换 ←→ 五 2 30 02 (a) (b) 图3-1星形(a)和三角形(b)接线

1. 网络的等值变换 （1）星网变换 (a) (b) 图3-1 星形(a)和三角形(b)接线

仁 五 02 Z= Z12Z31 12+Z23+Z31 乙=乙+23+☑☑ Z3 Z2= Z12Z23 二→ Z23=Z2+Z3+ Z2·Z3 Z12+Z23+Z31 Z Z3= Z23·Z31 Z1=Z3+Z1+ 3·Z Z12+Z23+Z31 Z2

⎪ ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎪ ⎬ ⎫ + + ⋅ = + + ⋅ = + + ⋅ = 12 23 31 23 31 3 12 23 31 12 23 2 12 23 31 12 31 1 Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z ⎪ ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎪ ⎬ ⎫ ⋅ = + + ⋅ = + + ⋅ = + + 2 3 1 31 3 1 1 2 3 23 2 3 3 1 2 12 1 2 Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z

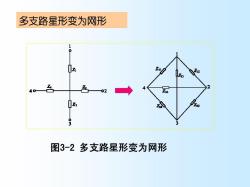
多支路星形变为网形 40 色 02 图3-2多支路星形变为网形

多支路星形变为网形 图3-2 多支路星形变为网形

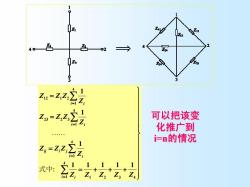
z 40 色 02 → lz, i=1 -2 可以把该变 化推广到 =n的情况 名-222法 式中：

⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎫ = + + + = = = ∑ ∑ ∑ ∑ = = = = 1 2 3 4 4 1 4 1 4 1 23 2 3 4 1 12 1 2 1 1 1 1 1 1 1 1 Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i ij i j i i i i 式中: K K 可以把该变 化推广到 i=n的情况

(2)有源支路的并联 it 的 (a) (b) 图3-3 并联有源支路的化简 Z

（2）有源支路的并联 图3-3 并联有源支路的化简 I Z E V m i i i & & & = − ∑ =1 (a) (b)

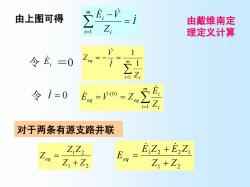
由上图可得 -=i 由戴维南定 Z 理定义计算 1 令龙，=0 令i=0 E=0=2 Z 对于两条有源支路并联 Z Z E Z2 +E2Z Z1+Z2 Z1+Z2

I Z E V m i i i & & & = − ∑ =1 由上图可得 由戴维南定 理定义计算 ∑ = = − = m i i eq Z I V Z 1 1 1 & & Ei 令 ＝ & 0 ∑ = = = m i i i eq eq Z E E V Z 1 (0) & 令 I& = 0 & & 对于两条有源支路并联 1 2 1 2 2 1 Z Z E Z E Z Eeq ++ = & & 1 2 1 2 Z Z Z Z Zeq + =