上海交通大学:《传热传质学 Heat and Mass Transfer》教学资源(课程讲义)Lecture Notes_hch6 INTRODUCTION(2/2)

Boundary Layer Similarity Parameters The boundary layer equations(velocity,mass, energy continuity)represent low speed,forced convection flow. Advection terms on the left side and diffusion terms on the right side of each equation, such as: Advection TT Diffusion W- Ox dy 0y2 Non-dimensionalize the equations by setting ond y where L is characteristic length of the surface and v-y where V is the freestream velocity (U) and T-T and P=p/pv2 T-T
Boundary Layer Similarity Parameters • The boundary layer equations (velocity, mass, energy continuity) represent low speed, forced convection flow. • Advection terms on the left side and diffusion terms on the right side of each equation, such as: Advection Diffusion • Non-dimensionalize the equations by setting: * s * 2 and / T T -T and where V is the freestream velocity ( ) where L is characteristic length of the surface P p V T T U V v and v V u u L y and y L x x s 2 2 y T y T v x T u

Boundary Layer Similarity Parameters(Cont'd) The boundary layer equations can be rewritten in terms of the non-dimensional variables Continuity ou,0* * =0 x-momentum aP O2u' +v Ox" ov" Ox L *2 a energy tv'o *dT* o2T u 元0y2 With boundary conditions Wall u(x,y=0)=0;v*(x,y=0)=0; T(x,y=0)=0 Frcestream:)U)if-U] T(x,y*=o)=1
Boundary Layer Similarity Parameters (Cont’d) • The boundary layer equations can be rewritten in terms of the non-dimensional variables Continuity x-momentum energy • With boundary conditions 0 * * * * y v x u 2 * 2 * * * * * * * * * y u x VL P y u v x u u 2 * 2 * * * * * * * y T y VL T v x T u ( , ) 1 [ 1if ] ( ) Freestream : ( , ) ( , 0) 0 Wall : ( , 0) 0 ; ( , 0) 0 ; * * * * * * * * * * * * * * * * T x y V U V U x u x y T x y u x y v x y

Boundary Layer Similarity Parameters(Cont'd) From the non-dimensionalized boundary layer equations,dimensionless groups can be seen Reynolds Prandtl Substituting gives the boundary layer equations: Continuity: ou'Ov" =0 * ou'ou ap* 1a2u* x-momentum: u +v Ox a" ReL oy Energy: aT,*∂T*1 02T dy" ReLPry2
Boundary Layer Similarity Parameters (Cont’d) • From the non-dimensionalized boundary layer equations, dimensionless groups can be seen Reynolds # Prandtl # Substituting gives the boundary layer equations: VL Re L 0 * * * * y v x u 2 * 2 * * * * * * * * * Re 1 y u x P y u v x u u L Re Pr 1 2 * 2 * * * * * * * y T y T v x T u L Continuity: x-momentum: Energy: P r

Back to the convection heat transfer problem... Solutions to the boundary layer equations are of the form: =,) dP" where: =0 for flat plate x* -小器 .Rewrite the convective heat transfer coefficient t 一k 6 T-T -ki h, 9 T。-I T,-T. T-T。 T-T. L kr 「a Define the Nusselt number as: Nu .o
Back to the convection heat transfer problem… • Solutions to the boundary layer equations are of the form: • Rewrite the convective heat transfer coefficient • Define the Nusselt number as: * * * * * * * * * * * * , ,Re ,Pr, , ,Re , where : 0 for flat plate dx dP T f x y dx dP dx dP u f x y L L L T T L y T T T T T T k T T y T k T T q h s y s s s f s y f s x x 0 0 0 * * * y f x y T L k h * * * 0 * * ,Re ,Pr, * dx dP f x y T L y Nu

Nusselt number for a prescribed geometry Nu= -=f(x'.Rec.Pr) Local Nu= _=f(Re.Pr) Average dp" (For a prescribed geometry, is known) dx Many convection problems are solved using Nusselt number correlations incorporating Reynolds and Prandtl numbers The Nusselt number is to the thermal boundary layer what the friction coefficient is to the velocity boundary layer. CI= 2 ou v2 → Re,dy" =0 2
Nusselt number for a prescribed geometry (For a prescribed geometry, is known) Many convection problems are solved using Nusselt number correlations incorporating Reynolds and Prandtl numbers • The Nusselt number is to the thermal boundary layer what the friction coef icient is to the velocity boundary layer. Re , Pr Average k hL , Re , Pr Local k hL f * f L L Nu f Nu f x * * dx dP * * * 0 * * 2 ,Re , Re 2 2 dx dP f x y u V C L L y s f
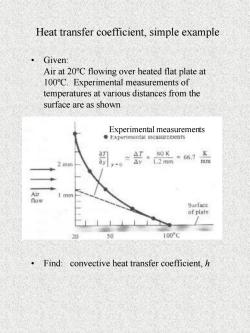
Heat transfer coefficient,simple example Given: Air at 20C flowing over heated flat plate at 100C.Experimental measurements of temperatures at various distances from the surface are as shown Experimental measurements Experiinental measurements 2 mm 1.2 mm =66.7 mm Air now Surface of plate 20 50 100C .Find:convective heat transfer coefficient,h
Heat transfer coefficient, simple example • Given: Air at 20ºC flowing over heated flat plate at 100ºC. Experimental measurements of temperatures at various distances from the surface are as shown • Find: convective heat transfer coefficient, h Experimental measurements

Heat transfer coefficient,simple example ·Solution: OT Rccall that h is computed by Ts-To From Table A-4 in Appendix,at a mean fluid temperature 7n7。+7 2 (average of free-stream and surface temperatures) Tm=(20+100)/2=60°C the air conductivity,k is=0.028 W/m-K ● Temperature gradient at the plate surface from experimental data is-66.7 K/mm =-66,700 K/m So,convective heat transfer coefficient is: h、 -0.028×(-66700) 80 W =23.345 m2K
Heat transfer coefficient, simple example • Solution: Recall that h is computed by • From Table A-4 in Appendix, at a mean fluid temperature (average of free-stream and surface temperatures) the air conductivity, k is 0.028 W/m-K • Temperature gradient at the plate surface from experimental data is -66.7 K/mm = -66,700 K/m • So, convective heat transfer coefficient is: 0 T T y T k h s y f x m K W 23.345 80 - 0.028 ( 66700) 2 h 2 m T Ts T T C m (20 100) 2 60

SUMMARY General boundary layer equations Ou av dx dy -0 u Bu 1 aP Ou u- +V =0 ay pox dy2 ay [=a 2T +V- Ox C 2 Nusselt number for heat transfer coefficient in the thermal boundary layer Nu= =f(.ReL.P) K Local Nu= L=f(ReL.Pr) Average Many convection problems are solved using Nusselt number correlations incorporating Reynolds and Prandtl numbers
• General boundary layer equations • Nusselt number for heat transfer coefficient in the thermal boundary layer • Many convection problems are solved using Nusselt number correlations incorporating Reynolds and Prandtl numbers. SUMMARY 0 y v x u 2 2 1 y u x P y u v x u u 0 y P 2 2 2 y u y c T y T v x T u p Re ,Pr Average ,Re ,Pr Local * L f L f f k h L Nu f x k h L Nu

Momentum and Heat Transfer Analogy IF WE CAN PUT A MAN YOUR FLAWED ANALO- MAYBE YOU SHOULD ON THE MOON,WE CAN GY ONLY SHOWS THAT CALL OTHER PEOPLE BUILD A COMPUTER OTHER PEOPLE CAN AND ASK HOW THEY MADE ENTIRELY OF DO OTHER THINGS. DO IT. RECYCLED PAPER. MAYBE THEY USE GOOD ANALOGIES Copyright 3 2002 United Feature Syndicate,Inc
Momentum and Heat Transfer Analogy

Momentum and Heat Transfer Analogy Where we've been...... Development of convective transport of heat transfer equations Where we're going: Momentum and heat transfer(Reynolds)analogy
Momentum and Heat Transfer Analogy Where we’ve been …… • Development of convective transport of heat transfer equations Where we’re going: • Momentum and heat transfer (Reynolds) analogy
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 上海交通大学:《传热传质学 Heat and Mass Transfer》教学资源(课程讲义)Lecture Notes_ch 8 Internal flow(2/2).ppt
- 上海交通大学:《传热传质学 Heat and Mass Transfer》教学资源(课程讲义)Lecture Notes_ch 8 Internal flow(1/2).ppt
- 上海交通大学:《传热传质学 Heat and Mass Transfer》教学资源(课程讲义)Lecture Notes_Ch 7 External flow.ppt
- 上海交通大学:《生物工程单元操作原理》课程教学资源_液液萃取_Extraction_2.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_液液萃取_Extraction_1.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_液体精馏_Equilibrium_6.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_液体精馏_Equilibrium_5.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_液体精馏_Equilibrium_4.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_液体精馏_Equilibrium_3.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_液体精馏_Equilibrium_2.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_液体精馏_Equilibrium_1.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_干燥_Drying 第四节 干燥器.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_干燥_Drying 第三节 干燥过程计算.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_干燥_Drying 第一节 概述 第二节 干燥静力学.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_气体吸收_Absorption_5.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_气体吸收_Absorption_4.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_气体吸收_Absorption_3.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_气体吸收_Absorption_2.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_气体吸收_Absorption_1.pdf
- 上海交通大学:《生物工程单元操作原理》课程教学资源_液体搅拌_液体搅拌.pdf
- 上海交通大学:《传热传质学 Heat and Mass Transfer》教学资源(课程讲义)Lecture Notes_hch6 INTRODUCTION(1/2).pdf
- 上海交通大学:《对流换热 Convection Heat Transfer》教学资源_教学资料_Chapter 6 and Appendix D Sections 6.1 through 6.8 and D.1 through D.3.pdf
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)微观和介观尺度的绿色工程——化学物质对生态环境和人类健康的影响(1/2).ppt
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)微观和介观尺度的绿色工程——化学物质对生态环境和人类健康的影响(2/2).ppt
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)概述、资源、环境与可持续发展(清华大学:韩明汉).ppt
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)微观和介观尺度的绿色工程——绿色化学(韩明汉).ppt
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)绿色单元(物流行业)绿色物流 Green Logistics(靳强).ppt
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)绿色单元操作(绿色化工).ppt
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)微观和介观尺度的绿色工程——绿色工程方案的评估和选择.ppt
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)绿色建筑整体解决方案.ppt
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)绿色过程(工业生产原理)Green Process(Industrial Process Principle).ppt
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)绿色过程(清洁生产审核案例)清洁生产审核汇报.ppt
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)通信行业节能减排综述及思路.ppt
- 上海交通大学:《绿色工程概论 Green Engineering》课程教学资源(PPT课件讲稿)绿色过程(清洁生产审核)Green Process(Clean Production Auditing).ppt
- 《催化学报》:(Ag/Al2O3+Cu/Ce(x)/AI2O3)组合催化剂催化乙醇选择性还原NOx及其副产物的消除.pdf
- 东莞理工学院:《专业综合实训一》课程教学资源(教学大纲)涂军令,元武智-20级化学工艺1班.doc
- 东莞理工学院:《专业综合实训一》课程教学资源(教学大纲)涂军令,元武智-20级能源化学1班.doc
- 东莞理工学院:《专业综合实训三》课程教学资源(教学大纲)涂军令,钟国玉-19级化学工艺1班.doc
- 东莞理工学院:《专业综合实训三》课程教学资源(教学大纲)涂军令,钟国玉-2019级能源化学工程1班.doc
- 东莞理工学院:《分析化学实验》课程教学资源(教学大纲)易莉芝楚家玉-2021化学工艺.docx
