安徽医科大学：《医药高等数学》课程教学资源（PPT课件讲稿）多元函数微积分学（二重积分）

4.7二重积分 4.7.1二重积分的概念 4.7.2二重积分的性质 4.7.3二重积分的计算 4.7.4二重积分的简单应用

4.7 二重积分 4.7.1 二重积分的概念 4.7.2 二重积分的性质 4.7.3 二重积分的计算 4.7.4 二重积分的简单应用

4.7.1二重积分的概念 问题的提出 曲顶柱体体积=？ 特点：平底曲顶 柱体体积=底面积×高 特点：平底平顶 3=f(x,y)

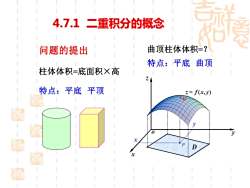
柱体体积=底面积×高 特点：平底 平顶 曲顶柱体体积=？ 特点：平底 曲顶 问题的提出 4.7.1 二重积分的概念

1.引例 (1)曲顶柱体顶体积. 设z=f(x,)是定义在有界区域D上的非负连续 函数，称以D为底，以D的边界为准线而母线平行于z 轴，以z=fcy),(Ky)∈D为顶部的立体图形为曲顶柱 体，求此曲顶柱体的体积八. 一

（1） 曲顶柱体顶体积. 设 z = f (x,y)是定义在有界区域D上的非负连续 函数,称以D为底,以D的边界为准线而母线平行于z 轴,以 z = f (x,y), (x,y)∈D为顶部的立体图形为曲顶柱 体,求此曲顶柱体的体积 V. 1. 引例

求曲顶柱体的体积采用“分割、近似、作和 取极限”的方法，如下动画演示 涵

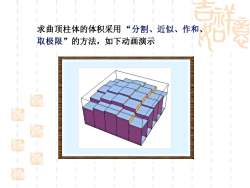
求曲顶柱体的体积采用 “分割、近似、作和、 取极限”的方法，如下动画演示

求曲顶柱体的体积采用“分割、近似、作和 取极限”的方法，如下动画演示 涵

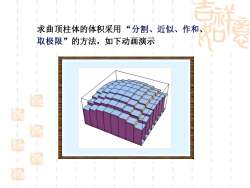
求曲顶柱体的体积采用 “分割、近似、作和、 取极限”的方法，如下动画演示

求曲顶柱体的体积采用“分割、近似、作和 取极限”的方法，如下动画演示 涵

求曲顶柱体的体积采用 “分割、近似、作和、 取极限”的方法，如下动画演示

求曲顶柱体的体积采用“分割、近似、作和 取极限”的方法，如下动画演示 涵

求曲顶柱体的体积采用 “分割、近似、作和、 取极限”的方法，如下动画演示

求曲顶柱体的体积采用“分割、近似、作和 取极限”的方法，如下动画演示 涵

求曲顶柱体的体积采用 “分割、近似、作和、 取极限”的方法，如下动画演示

求曲顶柱体的体积采用“分割、近似、作和 取极限”的方法，如下动画演示 涵

求曲顶柱体的体积采用 “分割、近似、作和、 取极限”的方法，如下动画演示

求曲顶柱体体积的方法： 分割、取近似、 求和、取极限。 z=f(x,y) (5i,) X

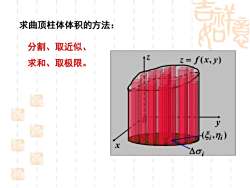
求曲顶柱体体积的方法： 分割、取近似、 求和、取极限。 x z y o D z = f (x, y) •  i ( , )  i i