《电磁学》课程教学资源（拓展资料）EM application Polarization and Conduction

6.641,Electromagnetic Fields,Forces,and Motion Prof.Markus Zahn Lecture 7:Polarization and Conduction I.Experimental Observation A.Fixed Voltage-Switch Closed (v=V) Switch Eo As an insulating material enters a free-space capacitor at constant voltage more charge flows onto the electrodes;i.e.as x increases,i increases. B.Fixed Charge-Switch open(i=0) As an insulating material enters a free space capacitor at constant charge, the voltage decreases;i.e.as x increases,v decreases. II.Dipole Model of Polarization A.Polarization Vector P=Np =Nqd (p=gd dipole moment) N dipoles/Volume (P is dipole density) d+q \-q 6.641,Electromagnetic Fields,Forces,and Motion Lecture 7 Prof.Markus Zahn Page 1 of 27

6.641, Electromagnetic Fields, Forces, and Motion Lecture 7 Prof. Markus Zahn Page 1 of 27 6.641, Electromagnetic Fields, Forces, and Motion Prof. Markus Zahn Lecture 7: Polarization and Conduction I. Experimental Observation A. Fixed Voltage - Switch Closed (v=Vo ) As an insulating material enters a free-space capacitor at constant voltage more charge flows onto the electrodes; i.e. as x increases, i increases. B. Fixed Charge - Switch open (i=0) As an insulating material enters a free space capacitor at constant charge, the voltage decreases; i.e. as x increases, v decreases. II. Dipole Model of Polarization A. Polarization Vector P Np Nqd = = (p qd = dipole moment) N dipoles/Volume (P is dipole density) d q + −q

No field Electric field E +9 F=gE d Torque =dx gE =pxE p=gd Electronic polarization Orientation and ionic polarization (a) (b) Figure 3-1 An electric dipole consists of two charges of equal magnitude but opposite sign,separated by a small vector distance d.(a)Electronic polarization arises when the average motion of the electron cloud about its nucleus is slightly displaced.(b)Orien- tation polarization arises when an asymmetric polar molecule tends to line up with an applied electric field.If the spacing d also changes,the molecule has ionic polarization. Courtesy of Krieger Publishing.Used with permission. + da dV d-da Surface S + AQ qNdV d.da >0 Positive charge leaves qNd-da b =P.da d.da o d.da <o Volume V 6.641,Electromagnetic Fields,Forces,and Motion Lecture 7 Prof.Markus Zahn Page 2 of 27

6.641, Electromagnetic Fields, Forces, and Motion Lecture 7 Prof. Markus Zahn Page 2 of 27 Courtesy of Krieger Publishing. Used with permission

QinsldeV=-∮qNd.da-∫ppdV paired charge or equivalently polarization charge density Q--.da--v-dv-odV (Divergence Theorem) P=qNd V.P=-Pp B.Gauss'Law V,e。目=poa=putp=pu-V.p unpaired charge density;also called free charge density V(e。E+p=pu D=8。E+p Displacement Flux Density V.D=Pu C.Boundary Conditions Ea,Pa,Da ⊙ Osur Osp Eo,Po,Do b 6.641,Electromagnetic Fields,Forces,and Motion Lecture 7 Prof.Markus Zahn Page 3 of 27

6.641, Electromagnetic Fields, Forces, and Motion Lecture 7 Prof. Markus Zahn Page 3 of 27 − =ρ ∫ ∫ i inside V P v S V Q = qN d da dV − =− ∇ = ρ ∫∫ ∫ i i inside V P v SV V Q = P da P dV dV P = qNd (Divergence Theorem) ∇ = −ρ iP P B. Gauss’ Law ∇ =ρ =ρ +ρ =ρ −∇ i i ( ) εo total u P u E P ∇ + =ρ i( ) εo u E P D EP o = + ε Displacement Flux Density ∇ =ρ iD u C. Boundary Conditions paired charge or equivalently polarization charge density unpaired charge density; also called free charge density

7.d=p→∮D.da=jp.dv→n[ba-b]=ou p=-p,→∮p.da=-∫P,dv→n[p-p]=-op e,目)=p。+p→∮8E.da-p。+po)dV→n[。-Ed]=u+p D.Polarization Current Density △Q=qNdV=qNd.da=p.da [Amount of Charge passing through surface area element da] di,-AQ-OP.da [Current passing through surface ot ot area element da] =Jp.da polarization current density -爱 Ampere's law: vx斤=j。+jn+8。t =3+OP +t+8。t =i+e.E+p可 -i+阳 6.641,Electromagnetic Fields,Forces,and Motion Lecture 7 Prof.Markus Zahn Page 4 of 27

6.641, Electromagnetic Fields, Forces, and Motion Lecture 7 Prof. Markus Zahn Page 4 of 27 ∇ ρ ⇒ ρ ⇒ − =σ ⎡ ⎤ ∫ ∫ ⎣ ⎦ ii i v a b u u su S V D = D da = dV n D D ∇ −ρ ⇒ − ρ ⇒ − = −σ ⎡ ⎤ ∫ ∫ ⎣ ⎦ ii i v a b P = P da = dV n P P PP sp ( ) ( ) a b o u P o u P o su sp S V ∇ =ρ +ρ ⇒ = ρ +ρ ⇒ − σ +σ E E da dV n E E = ⎡ ⎤ ⎣ ⎦ εε ε ∫ ∫ i ii v D. Polarization Current Density ∆= = = Q qN dV qN d da P da i i [Amount of Charge passing through surface area element da ] ∂∆ ∂ = = ∂ ∂ i p Q P di da t t [Current passing through surface area element da ] = J da p i polarization current density ∂ = ∂ p P J t Ampere’s law: u p o E xH J J t ∂ ∇ =++ ∂ ε ∂ ∂ =+ + ∂ ∂ u εo P E J t t ( ) ∂ =+ + ∂ u εo J EP t u D J t ∂ = + ∂ S V

III.Equipotential Sphere in a Uniform Electric Field →0 十十 E=Eoiz Eolir cose-iesine] limΦ(r,0)=-E。rcos0 [Φ=-Ez=-E。rcos0] Φ(r=R,0)=0 R3 cose This solution is composed of the superposition of a uniform electric field plus the field due to a point electric dipole at the center of the sphere: aple=Cos with p=4πeE.R3 4πe。r2 This dipole is due to the surface charge distribution on the sphere. aΦ cos0 =3e.E。c0s0 6.641,Electromagnetic Fields,Forces,and Motion Lecture 7 Prof.Markus Zahn Page 5 of 27

6.641, Electromagnetic Fields, Forces, and Motion Lecture 7 Prof. Markus Zahn Page 5 of 27 III. Equipotential Sphere in a Uniform Electric Field ( ) o oo r lim r, E r cos E z E r cos → ∞ Φ θ =− θ Φ=− =− θ ⎡ ⎤ ⎣ ⎦ Φ = θ= ( ) r R, 0 ( ) 3 o 2 R r, E r cos r ⎡ ⎤ Φ θ =− − θ ⎢ ⎥ ⎣ ⎦ This solution is composed of the superposition of a uniform electric field plus the field due to a point electric dipole at the center of the sphere: dipole 2 o p cos 4 r θ Φ = πε with 3 p 4 ER o o = πε This dipole is due to the surface charge distribution on the sphere. ( )( ) 3 s or o oo 3 rR rR 2R r R, E r R, E 1 cos r r = = ∂Φ ⎡ ⎤ σ = θ = = θ =− = + θ ⎢ ⎥ ∂ ⎣ ⎦ ε εε 3 E cos o o = ε θ

IV.Artificial Dielectric E V E-/G:-6ES d EA q=oA= d C=9=8A d 上● ●●●●●● Figure 6.6.1 (a)Plane parallel ●●●●●●● capacitor with region between ●●●●●● ● electrodes occupied by a dielectric. (b)Artificial dielectric composed of cubic array of perfectly conducting spheres having radius R and spacing (a) (b) Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. For spherical array of non-interacting spheres(s >R) p=4元8。R3E。i2→P2=Np2=4πE。R3E。N N=⅓ p=0 4π R s =y。8。E e(electric susceptibility) D=8E+P=8o[1+Ve]E=8E 8(relative dielectric constant) 8=8,6=6,1+v]=1+4(餐） 6.641,Electromagnetic Fields,Forces,and Motion Lecture 7 Prof.Markus Zahn Page 6 of 27

6.641, Electromagnetic Fields, Forces, and Motion Lecture 7 Prof. Markus Zahn Page 6 of 27 IV. Artificial Dielectric s v v E, E d d = σ= = ε ε s A qA v d =σ = ε = = q Aε C v d Courtesy of Hermann A. Haus and James R. Melcher. Used with permission. For spherical array of non-interacting spheres (s >> R) π⇒ π ε ε _ 3 3 z P = 4 R E i P = N p = 4 R E N oo z z oo N = 1 3 s ⎡⎤ ⎛ ⎞ ⎛⎞ ⎛⎞ ⎢ ⎥ π ψ ψπ ⎜ ⎟ ⎜⎟ ⎜⎟ ⎢ ⎥ ⎝⎠ ⎝⎠ ⎣⎦ ⎝ ⎠ ε ε 3 3 o eo e R R P= 4 E= E =4 s s ψe (electric susceptibility) + +ψ ⎡ ⎤ ⎣ ⎦ εε ε D= E P= 1 E= E o oe r ε (relative dielectric constant) ⎛ ⎞ ⎛ ⎞ ⎡ ⎤ +ψ + π ⎜ ⎟ ⎣ ⎦ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ε εε ε ε 3 ro o e o R = = 1 = 14 s _ d + ε E υ

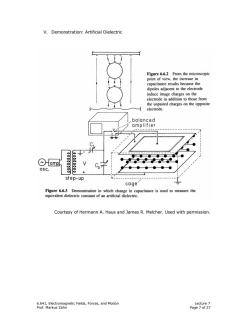
V.Demonstration:Artificial Dielectric Figure 6.6.2 From the microscopic point of view,the increase in capacitance results because the dipoles adjacent to the electrode induce image charges on the electrode in addition to those from the unpaired charges on the opposite electrode. balanced amplifier 心amp osc. 25555. step-up cage Figure 6.6.3 Demonstration'in which change in capacitance is used to measure the equivalent dielectric constant of an artificial dielectric. Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. 6.641,Electromagnetic Fields,Forces,and Motion Lecture 7 Prof.Markus Zahn Page 7 of 27

6.641, Electromagnetic Fields, Forces, and Motion Lecture 7 Prof. Markus Zahn Page 7 of 27 V. Demonstration: Artificial Dielectric Courtesy of Hermann A. Haus and James R. Melcher. Used with permission

Figure 6.6.4 Balanced amplifiers of oscilloscope,balancing capacitors,and demonstration capacitor shown in Figure 6.6.4 8 comprise the elements in the bridge circuit.The driving voltage comes from the transformer,while vo is the oscilloscope voltage. Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. E=首p,=eE=y d q=o,A=8Av→C=9=8A d d AC M sc.e-g.4合 d R=1.87cm,s=8cm,A=(0.4)2m2,d=0.15m @=2(250 Hz),Rs=100 k,V=566 volts peak △C=1.5pf V。=oACR,V =(2π)(250)(1.5×1012)(105)566=0.135 volts peak 6.641,Electromagnetic Fields,Forces,and Motion Lecture 7 Prof.Markus Zahn Page 8 of 27

6.641, Electromagnetic Fields, Forces, and Motion Lecture 7 Prof. Markus Zahn Page 8 of 27 Courtesy of Hermann A. Haus and James R. Melcher. Used with permission. s v v E= = E= d d ⇒ σ ε ε s A qA q= A= v C= = d vd σ ⇒ ε ε ∆ ω∆ o s v i= C V= R ( − ) ⎛ ⎞ ∆ π ⎜ ⎟ ⎝ ⎠ ε ε ε 3 o o A R A C= =4 d sd R=1.87 cm, s=8 cm, A= (0.4)2 m2 , d=0.15m ω =2π(250 Hz), Rs=100 k Ω , V=566 volts peak ∆ C=1.5 pf v = CR V 0 s ω ∆ =(2π) (250) (1.5 x 10-12) (105 ) 566 = 0.135 volts peak

VI.Plasma Conduction Model(Classical) m0=aE-mv文-R n m昨=-qE-mvV-p dt n p.=n.kT,p.=n_kT k=1.38 x 1023 joules/K Boltzmann Constant A.London Model of Superconductivity[T→O,v±→O] m..m. dt =-q.E dv- j.q.n,v,J=-q.n.v. 0-品an)=ang-ana目-E m.m 0+e 票-是an)qn祭-qng周-E m.m 06_8 @.=an,of.-92n (plasma frequency) m.E m 8 For electrons:q-=1.6 x 1019 Coulombs,m.=9.1 x 1031 kg n.=1020/m3,e=8。÷8.854x10-12 farads/,m 0p.=1 g2n≈5.6x101rad/s m.8 =2 g=≈9x100Hz 6.641,Electromagnetic Fields,Forces,and Motion Lecture 7 Prof.Markus Zahn Page 9 of 27

6.641, Electromagnetic Fields, Forces, and Motion Lecture 7 Prof. Markus Zahn Page 9 of 27 VI. Plasma Conduction Model (Classical) + + + + ++ + + ∇ −ν − dv p m =q E m v dt n − − − − −− − − ∇ − −ν − dv p m = qE m v dt n p = n kT , p = n kT ++ −− k=1.38 x 10-23 joules/o K Boltzmann Constant A. London Model of Superconductivity [ T → ν→ 0, 0 ± ] dv dv m =qE , m = qE dt dt + − ++− − − + − + − ++ −− J =q n v , J = qnv − ( ) ( ) q E 2 dJ d dv q n q n v =q n =q n = E dt dt dt m m + + + + + ++ ++ ++ + + + = ω + ε 2 p ( ) ( ) q E 2 dJ d dv q n = qnv = qn = qn = E dt dt dt m m − − − − − −− −− −− − − − − − −− ε 2 + + − − + − + − ω ω ε ε 2 2 2 2 p p q n q n = ,= m m (ωp = plasma frequency) For electrons: q-=1.6 x 10-19 Coulombs, m-=9.1 x 10-31 kg n-=1020/m3 , 12 o 8.854 x 10− ε = ≈ ε farads/m − − − − ω ≈ ε 2 11 p q n = 5.6 x 10 m rad/s − − ≈ π ωp 10 pf = 9 x10 2 Hz − ωp

B.Drift-Diffusion Conduction [Neglect inertia] 0 m -q.E-m.v.v.-V(n.kT)-v.-q.E-_kTVn. dt n. m,v.m.v.n, 0 --q.E-m.v.v.-Y(n.kT)=v.--q.E-_kTvn. dt n m_v.m.v.n. j.-q.n.v.-a.'n.E_gkT vn. m,v,m,v, j.=-q.n立=qE+akT vn. m_v. m_v P,=q,n,P.=-q.n. j,=p,μE-D,Vp J.=-p.H.E-D.Vp. 4,=9, m.v, D.=kT m.v, D.=kT m_v mv charge mobilities Molecular Diffusion Coefficients D.=D-=kT thermal voltage (25 mV @T=300 K) .q Einstein's Relation 6.641,Electromagnetic Fields,Forces,and Motion Lecture 7 Prof.Markus Zahn Page 10 of 27

6.641, Electromagnetic Fields, Forces, and Motion Lecture 7 Prof. Markus Zahn Page 10 of 27 B. Drift-Diffusion Conduction [Neglect inertia] 0 + ( + ) + + ++ + + + + + ++ +++ ∇ −ν − ⇒ − ∇ ν ν dv k T n kT q m =q E m v v = E n dt n m m n 0 − ( − ) − − − −− − − − − −− −−− ∇ − − −ν − ⇒ − ∇ ν ν dv k T n kT q m = qE m v v = E n dt n m m n ++ + + + ++ + ++ ++ − ∇ ν ν 2 q n qkT J =q n v = E n m m −− − − − −− − −− −− − +∇ ν ν 2 q n qkT J= qnv = E n m m ρ ρ− + ++ − −− =q n , = q n J= E D + ++ + + ρ µ − ∇ρ J= E D − −− − − −ρ µ − ∇ρ + + + ++ + + µ ν ν q k T = , D= m m − − − −− − − µ ν ν q k T = , D= m m charge mobilities D D k T = = q + − µ µ + − = thermal voltage (25 mV @ T ≈ 300o K) Einstein’s Relation Molecular Diffusion Coefficients